当前解决工业生产当中最优化问题较为热门的算法就是以遗传算法为代表的智能优化算法. 遗传算法以“优胜劣汰”的自然选择和基因阶段的遗传变异原理作为基础, 是一种具有很强的随机搜索能力的智能算法^[1]. 在解决多种复杂约束条件的寻优问题时, 可以取得很好的搜索效果. 但是在工业生产当中, 对算法的运行时间要求较为苛刻, 算法当中的种群数目较少, 在随机生成种群时个体很难遍布所有极值范围附近. 在前期的全局搜索过程中, 该算法很容易陷入局部最优, 从而无法对其他优秀解集区域进行搜索, 并且随着遗传操作的不断进行, 种群中的个体多样性将会不断降低. 因此解决遗传算法的“早熟”现象成为算法改进的主要方向.

为了解决“早熟”问题, 在遗传算法当中添加了灾变操作, 利用了灾变作用提高种群在遗传操作过程中全局搜索性能^[2]. 利用自适应遗传算法中交叉概率和变异概率随进化代数自适应调整的原理, 将交叉操作和变异操作随灾变周期进行自适应调整^[3], 在灾变完成之后, 提高个体的变异能力, 增强了算法的局部寻优能力. 将该算法应用于烧结配矿系统的建立, 利用生产数据进行检验, 证明了该算法可以搜寻到极为稳定且成本最优的配矿方案.

1 算法改进措施

通过大量的实验分析可得, 在解决具有多变量的最优化问题时, 遗传算法很容易因为遗传算法的特性造成“早熟”现象. 为了降低种群“早熟”现象的发生, 该模型在传统遗传操作过程当中添加了灾变操作. 灾变主要是模拟生物进化过程中导致大量物种灭绝而个别物种生存的现象^[4]. 在本算法中灾变操作周期性地强行对大部分个体进行初始化, 保留一定量的旧种群个体指导种群的搜索趋势, 并且在遗传操作中配合灾变操作的周期性变化进行自适应调整, 增强算法在后期种群个体相似度较高的时候搜索能力.

(1) 灾变操作

初始遗传种群的获得是通过未知量范围内的随机产生获得的, 假设一个种群遗传操作的代数为M时会使种群个体稳定, 当遗传操作到m(m<M)代之后, 大多数个体与最优个体相似度较高, 只有适应度较高的个体与最优个体相似度较低, 此时将当前种群状态和最优个体及其适应度进行保存, 将种群中大多数适应度优秀的个体进行删除, 随机产生新的个体进行补充, 只保留数量较少的原种群中适应度最差的个体保留之前的优秀种群特征组成新种群, 进行新一轮的搜索, 以此增大种群的多样性和搜索范围, 而灾变之后保留的旧种群个体由于本身处于较为优秀的寻优范围内会对新种群个体的搜索提供收敛趋势的引导. 本次寻优算法主要进行多次灾变操作, 并且当前一代灾变操作未能产生更为优秀个体时增大随机个体对进行灾变操作的种群个体的取代数量. 将种群重复m代的遗传操作, 当灾变操作完成时, 种群替换为n次灾变效果中取得最优秀个体的种群, 继续完成剩下的遗传操作, 灾变操作具体步骤如下所示.

① 对第i代种群进行判断, 如果为第一代种群, 即初始种群, 将该种群作为灾变保留种群进行保存, 将该种群中的适应度最优个体作为灾变最佳个体进行保存, 然后进行遗传操作. 判断代数i是否处于灾变截止代数 $N \times m$ 内, 如果是则进入步骤②, 如果进化代数i不处于灾变截止代数内则继续进行遗传操作.

② 判断种群进化代数i是否为设定的灾变操作代数, 如果是则进入步骤③, 否则继续进行遗传操作.

③ 当判断为灾变操作代数时, 将当前进化过m代之后的种群中的全局最佳适应度与灾变最佳个体的适应度进行比较, 如果全局最佳适应度更加优秀, 则将该全局最佳个体作为新的灾变最佳个体进行保存, 该进化种群作为新的灾变最佳种群进行保存, 然后将进化种群中根据适应度排序后的前pop个个体进行初始化处理, 然后将处理过的种群进行一定代数的遗传操作.

(2) 灾变周期自适应遗传操作

为了与灾变的周期性重复进行良好的配合, 该算法对交叉操作和变异操作进行改进, 令其随灾变过程周期性自适应变化, 增强算法从灾变开始到所有灾变操作完成过程当中对搜索范围的寻优能力. 在所有灾变操作完成之后, 种群个体已分布于各个极值的附近, 为了寻找到这些范围中的最优极值, 需要对这些优秀个体所处的局部范围进一步搜索. 本算法在灾变期间的寻优过程中跟随代数逐渐增大交叉、变异概率, 增大优秀个体间基因交流的可能性, 在灾变操作完成之后, 通过非线性函数的特点快速增大交叉、变异概率, 同时利用变异操作中变异范围的自适应缩小, 对每个个体的附近范围进行探索, 增强局部搜索能力.

① 灾变周期自适应交叉操作

通过对交叉概率进行自适应变化提高种群变异的全局搜索能力, 具体调整情况如下所示:

${P_c} = {K_1} + \frac{1}{{{K_2}}} \times \frac{1}{{1 + {e^{\frac{{M - (i - Num \times m)}}{{M - m}}}}}}$

(1)

${P_c}$ 是交叉概率, 上式当中Num为当前已发生的灾变次数. 种群每次进行m代遗传操作之后就进行一次灾变操作, 交叉概率 ${K_1}$ 为小于1的定值. 当 $i \ge w$ 时, 交叉概率进行自适应变化. ${K_2}$ 为一整数, 调节交叉概率的变化范围.

② 灾变周期自适应变异操作

变异操作是提高种群多样性的重要手段, 为了使种群在遗传操作后期, 收敛程度较高的时候增强种群的搜索能力, 提高种群基因多样性, 在改进算法当中对变异概率进行了关于迭代代数的自适应调整^[5], 使变异概率在完成灾变操作以后逐渐增大, 具体调整情况如下:

$\begin{array}{l} {P_{{m}}} = {K_3},i < w \\ {P_{{m}}} = {K_3} + \frac{1}{{K_4^{}}} \times \frac{1}{{1 + {e^{\frac{{V - {\rm{i}}}}{{V - w}}}}}},V > i \ge w \\ \end{array} $

(2)

式中, ${P_m}$ 是变异概率, w为m的N倍, 为停止所有灾变操作的截止代数, N为总灾变次数. 当i<w时, 种群每次进行m代遗传操作之后就进行一次灾变操作, 此时变异概率为小于1的定值 ${K_3}$ . 当 $i \ge w$ 时, 变异概率进行自适应变化, 并且不再进行灾变操作. 当执行了w代遗传操作之后, 将替换后的种群继续执行V–w代遗传操作, 对变异概率进行自适应调整, V为实际的总的迭代代数, ${K_4}$ 为一整数, 调节变异概率的变化范围.

变异操作方法是随机选择个体中的基因位置, 对被选中的基因 ${x_j}$ 进行如下自适应操作, 变异结果为 $x{_j'}$ :

$\left\{\begin{array}{l} {x_j}' = {x_j} + ({x_{j,max}} - {x_j}) \times {(1 - \frac{{i - m \times Num}}{M})^2} \times {r'} ,\;\;r > 0.5 \\ {x_j}' = {x_j} - ({x_j} - {x_{j,min}}) \times {(1 - \frac{{i - m \times Num}}{M})^2} \times {r'}, \;\;r \le 0.5 \\ \end{array}\right. $

(3)

式中, ${r'}$ , r为0~1之间的随机产生数, Num为发生变异操作时已经发生过的灾变操作的次数, m为灾变周期, M为遗传操作中种群的稳定周期, ${x_{j,min}}$ 和 ${x_{j,max}}$ 代表一个配矿方案中第j个变量的配比范围下限和上限.

2 算法仿真应用

为了检测改进算法的有效性, 本文利用钢厂的烧结配矿数据进行分析, 将寻找最低成本配矿方案为目的解析为最优化问题建立寻优模型. 所以此次寻优问题的目标就是在指定的约束条件下, 利用工人经验约束配比范围, 寻找成本最低的配矿方案. 该问题作为工业生产问题, 具有多变量、多约束条件、解集区域分布复杂等特点, 十分符合对改进算法的性能进行检测.

(1) 模型建立

当配料所使用的原料有n种时, 目标函数主要目的是计算每吨混合原料的成本cost元. 计算方式可以如下表示.

$cost = \frac{{\displaystyle\sum\limits_{j = 1}^n {{c_j}} \times {x_j} \times (1 - {H_2}{O_j})}}{{\displaystyle\sum\limits_{j = 1}^n {{x_j}} \times (1 - {H_2}{O_j}) \times (1 - Bur{n_j})}}$

(4)

式中, ${c_j}$ 表示的是第j种原料的吨单价(元); ${x_j}$ 表示第j种原料的配比, %, 成本cost, 元. ${H_2}{O_j}$ 为第j种烧结原料的水含量的百分比, %, $Bur{n_j}$ 为第j种烧结原料的烧损比, %.

配料的过程当中, 配料工作人员主要通过各种原料的库存量, 价格等因素配合自己在实际生产过程中积累到的经验对每种原料的配比进行范围约束, 同时保证所有的原料配比之和为1. 该约束条件的表达式如下所示:

$\left\{\begin{array}{l} {x_{j,min}} \le {x_j} \le {x_{j,max}} \\ \displaystyle\sum\limits_{j = 1}^n {{x_j}} = 1 \\ j = 1,2,\cdots,n \\ \end{array}\right. $

(5)

式中, ${x_{j,min}}$ , ${x_{j,max}}$ 表示第j种原料配比范围的上下限, %. 每种原料的配比 ${x_j}$ 范围主要通过初始化模型时对所有原料进行约束, 在执行遗传操作时始终保持种群中所有个体包含的配比处于各自的约束范围内. 为了降低算法的计算量, 配比和为1 的约束条件将会以惩罚项的形式添加到最终的适应度函数当中, 该惩罚项的建立形式如下所示.

$P = \beta |\sum\limits_{j = 1}^n {{x_j}} - 1|$

(6)

式中, 以 $\beta $ 作为惩罚因子, 是一个正整数, P为惩罚函数.

烧结矿当中各种化学成分和碱度是衡量烧结矿好坏的重要质量指标, 如果超出该范围会对钢铁质量和烧结设备造成严重影响. 第q种化学成分和碱度的约束条件如下所示:

${w_{q,min}} \le {w_q} \le {w_{q,max}}$

(7)

$P{H_{min}} \le \frac{{{w_{{\rm{C}}aO}}}}{{{w_{Si{O_2}}}}} \le P{H_{\max }}$

(8)

式中, ${w_q}$ 为计算出的烧结矿中第q种元素的含量(%). 同时 $P{H_{min}}$ , $P{H_{max}}$ 是碱度的上下限(%), 碱度定义为烧结矿中氧化钙和二氧化硅的含量之比. 化学成分和碱度的约束条件也将以惩罚项的形式添加到最终的适应度函数当中, 惩罚项建立方法如下:

$\begin{align} W = & \partial \times \{ max{\rm{[(}}{w_q}{\rm{ - }}{w_{q,min}}),0] \\ + & max{\rm{[(}}{w_{q,\max }}{\rm{ - }}{w_q}),0]\} \\ + & \theta \times \{ max{\rm{[(}}\frac{{{w_{CaO}}}}{{{w_{Si{O_2}}}}}{\rm{ - }}P{H_{min}}),0] \\ + & max{\rm{[(}}P{H_{max}}{\rm{ - }}\frac{{{w_{CaO}}}}{{{w_{Si{O_2}}}}}),0]\} \\ \end{align} $

(9)

式中, 的两个惩罚因子 $\partial $ 、 $\theta $ 为正整数, W为惩罚项.

最佳个体将会成为通过搜索遗传过程中所有个体当中适应度最小的个体. 适应度函数的建立如下所示, 当一个配矿方案的各项约束超出范围情况越严重时惩罚程度就会越大, 适应度就越大.

$F = cost + P + W$

(10)

(2) 编码方案

基于烧结原料的种类十分丰富, 每次生产前所需配料的种类有十几种, 所以为了降低计算量, 节省计算时间, 算法中采用实数编码方式, 以多个实数组成种群中的个体.

(3) 选择方法

随机产生的初始种群的个体适应度差别不大, 难以通过轮盘选择等方法对个体进行选择. 该遗传算法通过此特点对选择方法进行改进, 使其更好的选取优秀个体, 引导收敛方向, 具体选择方法如下:

先将所有个体按照适应度由小到大的顺序进行排序, 对前25%个体数量翻倍, 组成新种群前50%的个体, 前25%到50%的个体直接放入新种群中. 计算种群中所有个体与当前全局最佳个体的相似度, 对个体基于相似度由大到小排序, 选择与当前最优个体相似度高的个体对种群进行补全, 相似度计算采用欧氏距离计算方法^[6], 计算公式如下所示:

$D = \sqrt {\sum\limits_{j = 1}^n {{x_j} - {x_{best,j}}} } $

(11)

式中, D表示相似度, n表示个体中所有的基因个数, ${x_{best,j}}$ 是当前搜索到的最佳方案中第j种原料的配比(%).

(4) 交叉操作

需要配比的原料有十几种, 所以该问题是一种多维求解的问题, 而且通过大量实验发现优秀解集都处于一个相对较小的范围当中. 种群中每个个体含有多种变量, 和采用二进制编码的种群个体具有一定的相似性. 该算法通过对不同个体进行随机选择多个位置, 交换相同位置上的基因实现交叉操作^[7]. 这种方法可以利用现有的种群基因增强种群的多样性, 同时又不会使种群中的个体逃离当前的最优解集范围, 在该问题的研究当中取得了很好的效果,具体的交叉方式如下图所示, 两个被随机选择出的个体S和个体K,在给两个个体中随机选择出若干个基因位置, 将两个个体相同基因位置上的基因进行交换. 结果见图1.

改进的遗传算法的主要执行步骤如图2所示.

3 仿真结果对比

在解决这种非线性寻优问题时, 遗传算法、蚁群算法、差分算法、粒子群算法是最为常用的几种智能进化算法. 为了验证改进的遗传算法的寻优效果, 本文以河北某钢厂的实际生产数据作为试验数据进行测试, 设置算法种群个体数为200, 迭代代数为250, 每进行50代遗传操作之后进行一次灾变操作, 直到完成250代的所有遗传操作为止, 交叉概率设为0.5, 变异概率设为0.4. 表1为钢厂工程师总结出的烧结矿成分范围作为约束条件, 分别使用灾变自适应遗传算法和自适应遗传算法^[8,9]、蚁群算法、差分算法、粒子群算法进行寻优测试, 进行仿真对比^[10].

以某一日期数据进行试验为例, 多种算法的实际寻优效果如图3–图7所示, 纵轴代表成本(元), 横轴代表迭代代数.

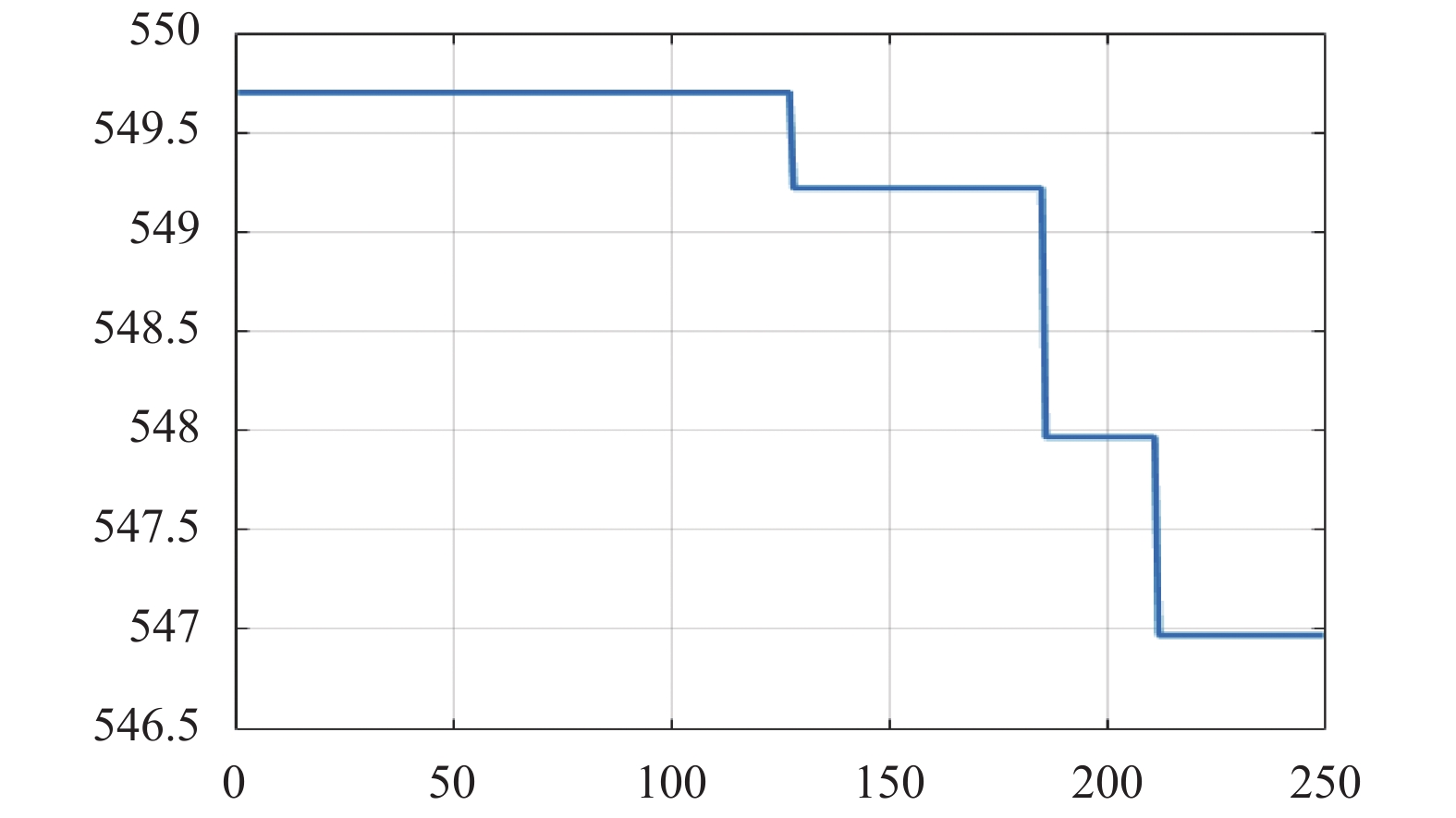
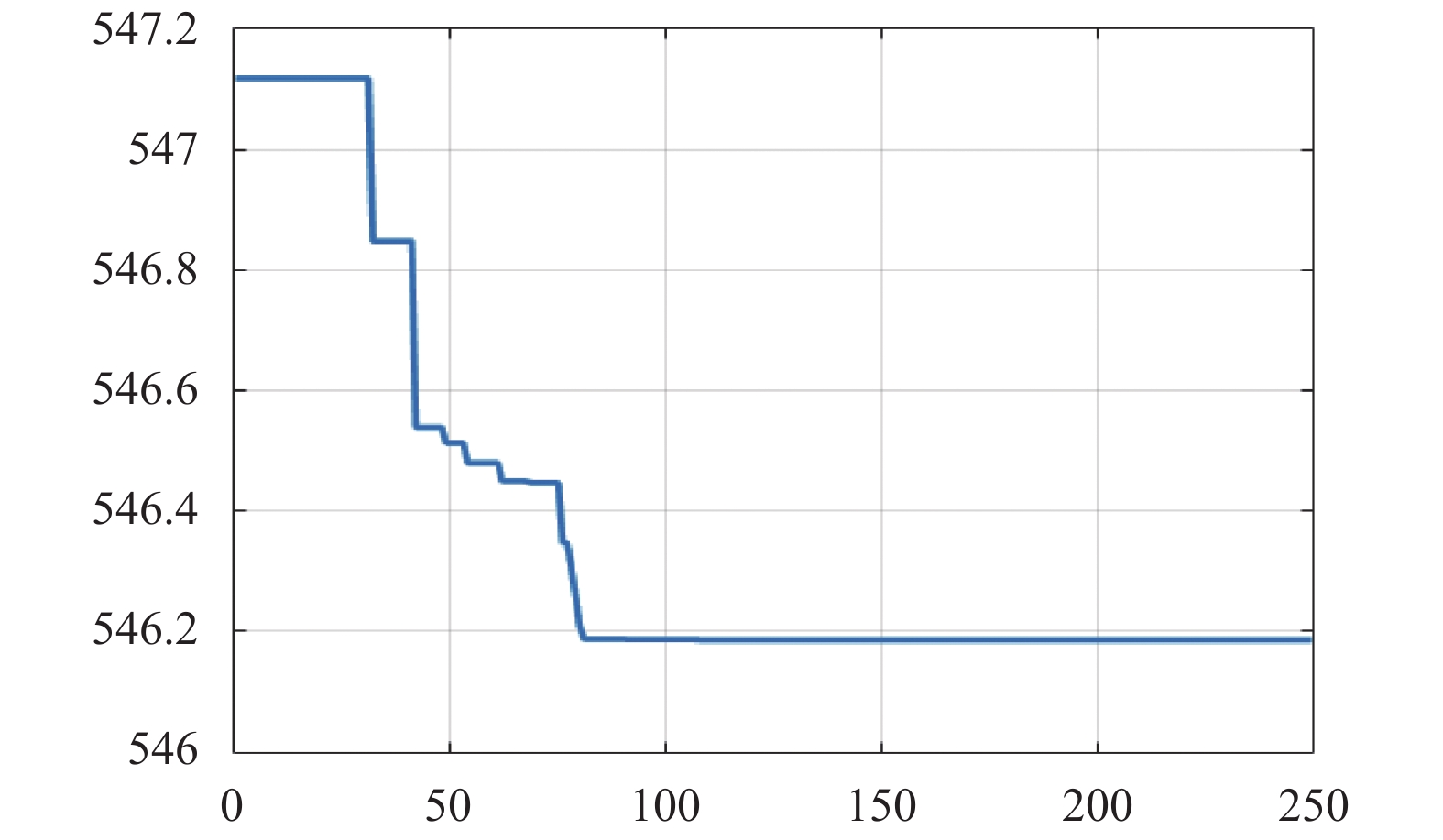
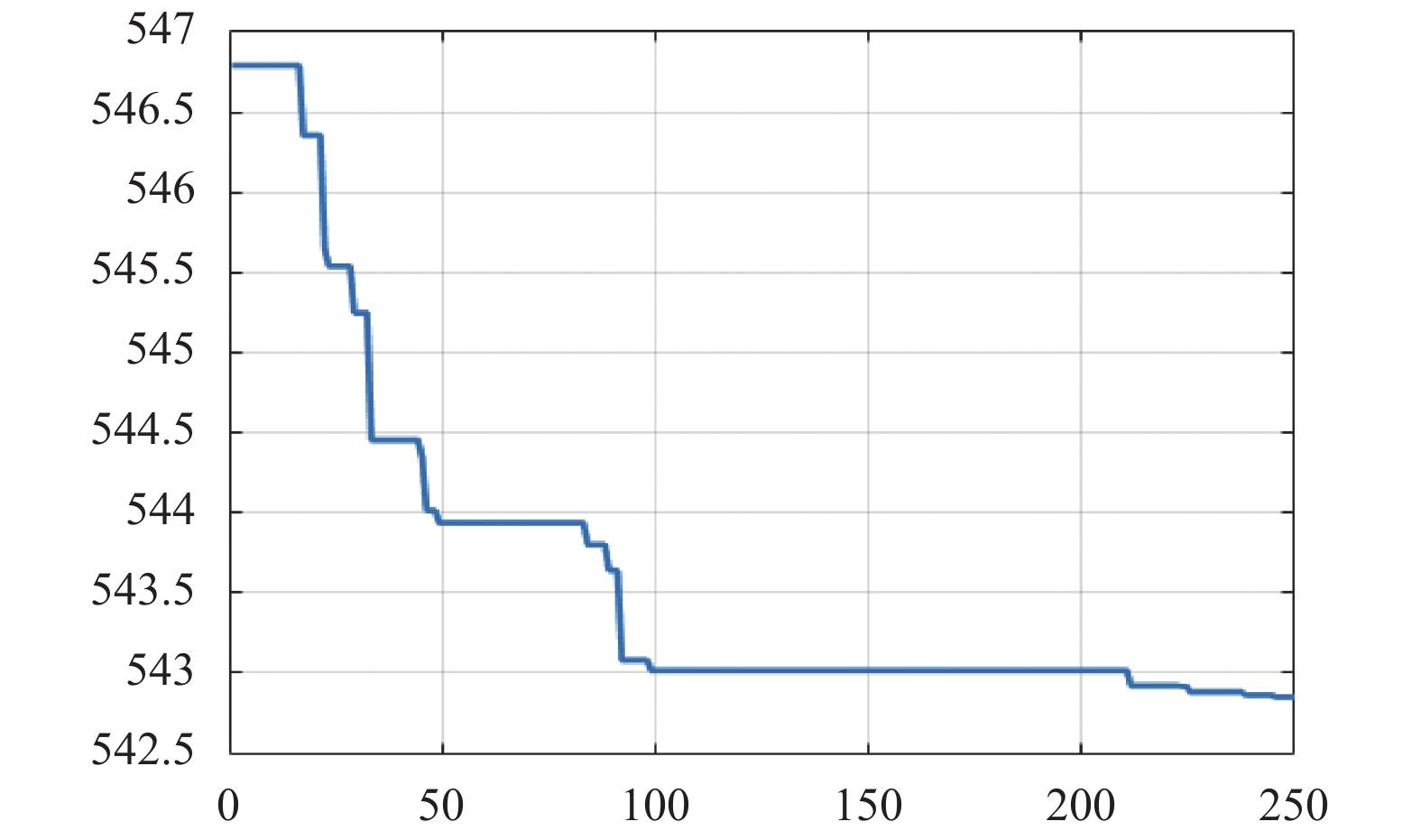
通过图3与图4至图6相比较, 自适应遗传算法在最优方案的搜索效果上要优于蚁群算法、差分算法和粒子群算法, 但是在执行了130代遗传操作之后, 寻优结果基本稳定在544.75(元)附近, 此时种群趋于“成熟”无法搜索到更加优秀的个体. 而与图7的灾变遗传算法相比较, 可以明显的看到, 在前200代遗传操作中因为添加了灾变操作, 根据灾变周期自适应调整的遗传算略可以增强遗传算法的全局搜索效果, 实际搜索范围覆盖的更加完整, 比自适应遗传算法更高效地搜索优秀个体区域, 获得更优个体, 充分说明了全局搜索效果更佳, 搜索结果更优秀. 完成所有的灾变操作之后, 在200代到250代遗传操作过程中, 配合交叉和变异操作的自适应调整, 搜索范围快速收敛, 在种群个体相似度较高的情况下随代数增多个体间的基因交流, 逐步降低变异范围, 增大了个体在局部范围的搜索能力, 进一步优化搜索结果, 如图7所示取得了更加优秀的效果.

同时将各个算法的寻优结果当中烧结矿的化学成份进行对比, 结果如表2所示, 可以看到, 灾变自适应遗传算法遗传算法可以在保证烧结矿质量指标的前提下, 有效地降低原料成本.

如表3所示的最优配矿方案与钢厂企业的生产方案计算数据相比较, 可以看到基于灾变的自适应遗传算法可以在有效的经验配比范围内得到成本优于企业人工配比的方案.

4 结束语

该改进遗传算法通过特殊的选择方法和交叉方法将搜索范围不断向优秀搜索区域靠拢, 同时通过变异概率的后期自适应变化, 增强了局部搜索能力, 为优秀解的选择奠定了基础, 而灾变操作的加入, 增强了算法的全局搜索能力, 解决了传统遗传算法的“早熟”问题, 很好的在全区域内进行搜索, 有利于全局最优解的确定. 针对烧结配矿的成本最低问题, 结合烧结矿的各种非线性的质量指标约束, 该改进算法的寻优结果十分稳定. 通过上述数据对比结果可知, 该算法可以明显的改善配料方法, 而且寻优配矿方案经钢铁企业验证可以在满足企业生产的情况下降低原料成本, 为钢铁企业带来很好的经济效益.