引言

车辆路径问题是指在一个存在供求关系的系统中, 在一定的约束条件下, 合理安排车辆的行车路线和出行时间, 把客户需求的货物从配送中心送达客户, 并使目标函数取得最优化^[1]. 随着研究的深入和实际应用场景的需求, 增加了对客户偏好服务时间的约束, 即个性化地限定了客户被服务时间的范围, 延伸出了带时间窗的车辆路径问题(VRPTW), 在实际生产应用中有广泛应用, 比如O2O外卖配送、冷链物流、生产线上的工作调度、网络路由策略等.

VRPTW是NP-hard的组合优化问题^[2], 计算复杂度高, 难以有效率地使用精确算法求得最优解, 目前的研究大多集中在如何设计高质量的启发式算法, 求取近似解以换取计算效率的提高, 如蚁群算法^[3]、粒子群算法^[4]、遗传算法^[5]、模拟退火等群体智能算法. 目前算法研究主要集中于两方面, 一是提升VRPTW的求解精度, 二是提升计算速度.

现阶段VRPTW求解存在的问题是: (1)算法过早收敛, 易陷入局部最优解; (2)相较于集中式节点分布, 算法对随机分布的节点处理精度差; (3)算法能处理的节点数少, 一般为100节点之内; (4)面对大规模问题出现单机处理效率瓶颈, 忽视使用分布式平台进行并行计算^[6]. 针对上述问题, 本文对蚁群算法进行改进, 基于Spark平台进行编程求解VRPTW, 在Solomon benchmark和Gehring & Homberger benchmark上进行实验, 为快速有效地求解大规模VRPTW提供了一种新思路.

1 传统蚁群算法求解VRPTW 1.1 VRPTW多目标0-1规划模型

VRPTW可被定义为: 某物流配送网络中, 记 $0$ 为配送中心, $\{ 1,2,\cdots,n\} $ 为 $n$ 个待配送客户点, 已知各客户点的位置坐标为 $({x_i},{y_i})$ 、货物需求为 ${D_i}$ , 允许的开始服务时间窗为 $[S{T_i},E{T_i}](i = 1,2,\cdots,n)$ , 安排装载能力为 $Q$ 的 $m$ 辆车从 $0$ 出发, 共同完成对 $n$ 个客户的配送后回到起点 $0$ , 优化目标是最小化配送路径长度和车辆数目.

由上述定义可知, VRPTW是一个离散组合优化问题, 我们将其抽象为多目标0-1规划问题^[6], 其数学模型具体如下:

决策变量:

${x_{ijk}} = \left\{ \begin{array}{l} 1,\;\;{\text{车辆}}{{k}}{\text{选择路径}}\;({{i}},{{j}})\\ 0,\;\;{\text{其它}} \end{array} \right.$

(1)

目标函数:

$Z = \min \left({\rho _1}\sum\limits_{k = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{l_{ij}}{x_{ijk}} + {\rho _2}\sum\limits_{k = 1}^m {\sum\limits_{j = 1}^n {{x_{0jk}}} } } } } \right)$

(2)

约束条件:

$ \sum\limits_{j = 1}^n {{x_{0jk}} = 1}\;\;{\text{且}}\;\; \sum\limits_{i = 1}^n {{x_{i0k}} = 1} ,\forall k $

(3)

$ \sum\limits_{k = 1}^m {\sum\limits_{j = 0}^n {{x_{ijk}}} } = 1,\forall i $

(4)

$\sum\limits_{i = 0}^n {\sum\limits_{j = 0 \wedge j \ne i}^n {{D_i}{x_{ijk}}} } \leqslant Q,\forall k$

(5)

$S{T_i} < {t_i} < E{T_i},\forall i$

(6)

$ {x_{ijk}} \in \{ 0,1\} ,\;\forall i,j,k $

(7)

式(2)中 ${l_{ij}}$ 为点 $i$ 和点 $j$ 间路径长度, ${\rho _1}$ 和 ${\rho _2}$ 分别为目标函数中路径长度和车辆数目的优化重要度, 如 ${\rho _1} \in [0,1]$ 越大则表示以路径长度最短为第一目标. 约束目标中式(3)表示车辆从 $0$ 出发并回到 $0$ 形成闭环; 式(4)表示各客户点有且只有一辆车对其服务; 式(5)表示各车辆的载重约束; 式(6)表示时间窗约束; 式(7)表示决策变量为0-1变量.

1.2 传统蚁群算法求解VRPTW

蚁群算法启发于真实蚂蚁自组织的觅食行为^[3], 对VRPTW这种难解的离散优化问题有优秀的求解能力, 得益于正负反馈机制的协同作用和其并行性. 核心思想是: 单只蚂蚁在其走过的路径上释放信息素, 根据信息素浓度和启发式信息决策转移路径; 蚂蚁之间通过信息素进行通信, 单次迭代后信息素进行挥发且增加优秀路径上的信息素浓度, 使得大概率选择目前优秀解的同时扩展搜索范围, 通过多只蚂蚁间相互协作多次迭代寻优.

蚁群算法是构建解和更新信息素的相互作用^[7], 具体如下:

(1)构建解: 通过计算状态转移概率逐步构建完整解后, 对解进行评估. 状态转移概率公式见式(8):

$ {p_{ij}} = \left\{ \begin{aligned} & \dfrac{{\tau _{ij}^\alpha \eta _{ij}^\beta }}{{\displaystyle\sum\limits_{j \in allowe{d_i}} {\tau _{ij}^\alpha \eta _{ij}^\beta } }},\;{\rm{if}}\;\;j \in allowe{d_i}\\ \;\; & \;\;\;\;\;\;\;\;\; 0,\;\;\;\;\;\;\;\;\;{\text{否则}} \end{aligned} \right. $

(8)

其中, ${p_{ij}}$ 表示由节点 $i$ 选择转移到节点 $j$ 的概率; ${\tau _{ij}}$ 表示路径 $(i,j)$ 上的信息素浓度; ${\eta _{ij}}$ 表示路径 $(i,j)$ 的启发式因子, 通常是路径长度的倒数; $\alpha $ 和 $\beta $ 分别表示信息素和启发式因子的重要程度.

(2)更新信息素: 一次迭代后, 根据解评估结果更新信息素浓度, 之后继续迭代寻优. 信息素更新包括追溯增加和挥发减少两种, 具体见式(9):

$\left\{ \begin{gathered} {\tau _{ij}}(t + 1) = \rho {\tau _{ij}}(t) + \vartriangle {\tau _{ij}}(t,t + 1) \\ \vartriangle {\tau _{ij}}(t,t + 1) = \sum\limits_{k = 1}^m {\vartriangle \tau _{ij}^k(t,t + 1)} \\ \end{gathered} \right.$

(9)

其中, 蚂蚁 $t$ 时刻位于节点 $i$ , $t + 1$ 时刻位于节点 $j$ , $\rho $ 表示残留因子, $\vartriangle {\tau _{ij}}(t,t + 1)$ 表示信息素增量, $\vartriangle \tau _{ij}^k(t,t + 1)$ 表示第 $k$ 辆车信息素增量, 通常为 $1/{C_k}$ , ${C_k}$ 为第 $k$ 辆车路径总长度.

传统蚁群求解VRPTW仍存在引言中提到的4个共性问题, 为了避免陷入局部最优, 提升各类点分布和大数据下的求解精度和速度, 下面提出基于Spark平台的改进蚁群算法求解VRPTW.

2 基于Spark的改进蚁群算法求解VRPTW 2.1 算法思路

本文采用基于Spark的改进蚁群算法求解带时间窗车辆路径问题, 该算法从算法层和实现层进行改进, 在算法层面, 通过改进状态转移规则^[8]、加入轮盘赌选择机制、结合k-opt邻域搜索^[9]进行路径构建优化, 改进最大最小蚁群中的信息素更新策略, 在实现层面, 用Spark计算平台对改进蚁群算法并行实现, 采用Spark提供的API对蚁群弹性分布式数据集(Resilient Distributed Dataset, RDD)进行操作, 实现蚁群并行构建解的过程.

2.2 路径构建优化

蚁群算法是从最初的空解开始, 逐步添加解成分直到构建完整解, 只能生成数量有限的解, 邻域搜索最初依赖一个好的初始解, 不断通过局部调整尝试改进当前解. 本文采用蚁群算法和邻域搜索相结合的方式进行路径构建, 通过状态转移规则和轮盘赌选择机制构建初始解后, 使用邻域搜索进行局部优化获得高质量解.

针对VRPTW问题, 由于增加了时间窗约束, 因此状态转移规则除了以信息素浓度高、路径长度小为优先选择原则外, 还要在满足车载限制和时间窗的前提下, 以等候时间短、时间窗紧为优先选择原则, 则蚂蚁由节点 $i$ 选择转移到节点 $j$ 的概率见式(10):

$ {p_{ij}} = \left\{ \begin{aligned} & \dfrac{{\tau _{ij}^\alpha \eta _{ij}^\beta }}{{\sum\limits_{j \in allowe{d_i}} {\tau _{ij}^\alpha \eta _{ij}^\beta } }}*\dfrac{{1/(|{t_{ij}} - S{T_j}| + |{t_{ij}} - E{T_j}|)}}{{\sum\limits_{j \in allowe{d_i}} {1/(|{t_{ij}} - S{T_j}| + |{t_{ij}} - E{T_j}|)} }},\\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;j \in allowe{d_i}\\ & \;0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{其它}} \end{aligned} \right. $

(10)

记 ${t_{ij}}$ 为到达节点 $j$ 的时间, 当 ${t_{ij}} \geqslant S{T_j}$ 时, 等待时间为 $0$ , $|{t_{ij}} - S{T_j}| + |{t_{ij}} - E{T_j}|$ 为时间窗大小, 否则当 ${t_{ij}} < S{T_j}$ 时, $|{t_{ij}} - S{T_j}| + |{t_{ij}} - E{T_j}|$ 为时间窗和等候时间的综合指标.

在式(10)中参数 $\alpha $ 和 $\beta $ 的作用如下: $\alpha $ 和 $\beta $ 分别表示信息素和启发式因子的相对重要程度, 如果 $\alpha = 0$ , 则算法未使用信息素, 而大概率地选择距离最近的节点, 属于随机贪心算法; 如果 $\beta = 0$ , 则算法没有任何启发式信息带来的偏向性, 特别是当 $\alpha > 1$ 时, 所有蚂蚁按照最初信息素浓度最大的同一条路径移动, 算法很快停滞于一个精度很差的解. 因此这里选择最大最小蚁群算法(MMAS)具有良好性能的参数设置: $\alpha $ 取值1~2, $\beta $ 取值2~5.

若每次迭代均按照状态转移规则 ${p_{ij}}$ 直接选择最大概率的节点作为下一个待配送客户, 则信息素向局部最优路径聚集, 使算法过早收敛停滞于次优解, 为了增加算法随机性, 本文使用轮盘赌选择机制对路径构建进行优化, 具体做法是: 随机选取一个实数 $T \in [0,1]$ , 分别减去各候选节点被选择的概率 ${p_{ij}}$ , 若 $T - {p_{ij}} \leqslant 0$ , 则选择城市 $j$ 作为下一个配送节点, 否则重复上述过程.

因此每只蚂蚁的搜索过程是从候选节点中依据改进的状态转移规则并采用轮盘赌选择机制选择下一个待服务的节点, 逐步添加解成分直至构成完整初始解, 相较于传统蚁群算法的初始解构建过程该方法可以得到更合理的初始解, 状态转移规则改进后使得减少配送过程中车辆的等待时间并能根据顾客的具体时间需求调配配送方案, 轮盘赌选择机制增强了初始解选择的随机性, 使得各节点均有概率被选中且被选择的可能性与其状态转移概率成正比, 能保持发现新路径的能力, 避免算法陷入局部最优.

获得完整初始解后, 通常用k-opt(k=2, 3)局部搜索策略对当前解邻域进行局部调整优化, 核心思想是任意选取 $k$ 个点 $(a,b,\cdots,k)$ , 删除当前解中的相应 $k$ 条边 $[(a,a + 1),(b,b + 1),\cdots,(k,k + 1)]$ , 替换为相关节点重组的另外 $k$ 条边以期获得更优解, 若当前解满足 $k$ 最优, 则对 ${k'} < k$ 一定也满足最优^[10], k-opt的时间复杂度为 ${\rm{O}}({n^k})$ , $k$ 越大时虽然效果越好但耗费的计算时间近似指数级增长^[11], 本文采用Lin和Kernighan提出的Lin-Kernighan(LK算法)局部搜索策略处理大规模数据, 在时间和求解效率间取得较好的平衡, LK算法通过迭代、回溯不断寻找边 ${y_i}$ 代替初始路径的边 ${x_i}$ , 构成序列 $X = [{x_1},{x_2},\cdots,{x_r}]$ 和 $Y = [{y_1},{y_2},\cdots,{y_r}]$ , 其中 $r$ 不固定, 是此序列的最大长度, 具体的算法流程如图1所示.

2.3 信息素更新优化

通过上述路径构建方法, 每只蚂蚁已经可以得到VRPTW问题的一个较优可行解, 但是要想获得精度高的解, 还需要群体进行分布式学习的过程, 蚂蚁之间通过每轮迭代后的信息素更新来交互协作, 其中信息素初始化、蒸发策略、更新策略都会影响算法寻优能力^[12].

本文选择最大最小蚁群算法(MMAS)中的信息素更新策略, 强调对最优路径区域的搜索, 每轮迭代后只选择一只构建出最优路径的蚂蚁释放信息素, 最优路径分为迭代最优 ${T^{\rm{Ibest}}}$ 和全局最优 ${T^{\rm{Gbest}}}$ , 使用全局最优更新规则会使得搜索加速集中到 ${T^{\rm{Gbest}}}$ 附近, 而使用迭代最优规则能相对减弱搜索导向性^[13]. 针对节点数较多的情况, 本文采用 ${T^{\rm{Ibest}}}$ 和 ${T^{\rm{Gbest}}}$ 轮流进行更新的策略.

信息素蒸发策略使得所有路径上的信息素均随时间而衰减,避免信息素在某些边上无限积累或者快速减少^[14]. 传统蚁群算法中的信息素蒸发因子 $1 - \rho $ 为一个常数, 当 $\rho $ 过大时, 信息素留存持久度高, 信息素在当前局部最优路径上聚集, 正反馈作用增强, 全局搜索能力差, 当 $\rho $ 过小时, 信息素衰减过快, 留存时间少, 信息素在路径选择过程中的作用降低, 最终会导致算法收敛性降低, 搜索时间过长且找不到最优路径. 为了平衡全局搜索和正反馈寻优能力, 解决在迭代中后期出现长期找不到新的全局最优解的问题, 本文采用一种自适应信息素蒸发策略, 见式(11), 具体为在迭代初始采用较大的信息素残留因子 ${\rho _{\max }}$ , 加速收敛且增强寻优能力, 随后当全局最优解的搜索停滞超过总迭代次数的1/10时, 自适应减少残留因子, 扩大搜索范围, 同时设置残留因子的最小值 ${\rho _{\min }}$ . 这里取最大残留值 ${\rho _{\max }} = 0.9$ , 最小残留值 ${\rho _{\min }} = 0.5$ , 由于搜索停滞超过总迭代次数的1/10时残留因子自适应衰减, 则至多衰减10次, 因此衰减系数为 $\sqrt[{10}]{{{\rho _{\min }}/{\rho _{\max }}}} = 0.95$ .

$ \rho = \left\{ {\begin{array}{*{20}{l}} {0.9,} & {{\rho _{\max }}}\\ {0.95 * \rho ,} & {{\text{停滞}}}\\ {0.5,} & {{\rho _{\min }}} \end{array}} \right. $

(11)

通过信息素择优和衰减策略可以确定一轮迭代后每条路径上的信息素浓度 ${\tau _{ij}}$ , $t$ 次迭代后 ${\tau _{ij}}$ 的值为 ${(1 - \rho )^t}{\tau _0} + \sum\limits_{i = 1}^t {{{(1 - \rho )}^{t - i}}C_i^{\rm{best}}} $ , 各条路径上的信息素浓度差值过大会造成所有蚂蚁向局部最优路径聚集, 为了避免算法陷入停滞, 这里采用MMAS中对信息素浓度大小的限制 $[{\tau _{\min }},{\tau _{\max }}]$ , 见式(12).

$ \left\{ \begin{aligned} &{\tau _{\max }} = 1/(1 - \rho ){C^{\rm{best}}} \\ &{\tau _{\min }} = {\tau _{\max }}(1 - \sqrt[n]{{0.05}})/(n/2 - 1) \\ \end{aligned} \right. $

(12)

信息素初值 ${\tau _0}$ 一般将其设为略高于每次迭代中蚂蚁释放的信息素大小的期望值, 若 ${\tau _0}$ 太小, 信息素更新会有较强的引导性作用, 搜索会快速集中到最初产生的几条路径上, 导致搜索陷入局部空间, 若 ${\tau _0}$ 太大, 迭代初始阶段收敛速度慢, 直到信息素衰减后更新才开始发挥作用. 本文取 ${\tau _0}$ 为 ${\tau _{\max }}$ , 使得在循环初始阶段, 具有很强的探索性.

2.4 基于Spark平台并行化

目前VRPTW问题的许多实际应用面对爆炸式的数据增长和实时性求解的要求, 出现单机求解的效率瓶颈, 而蚁群算法是一个分布式学习的过程^[15], 有内在的并行性, 每次迭代中多只蚂蚁独立的根据规则同时同地的构建可行解, 因此本文将基于Spark分布式平台来实现该算法.

Spark是一个快速且通用的集群计算平台, 扩充了Map-Reduce计算模型, 与Hadoop不同的是多个任务之间数据通信不需要借助硬盘而是通过内存, 减少了IO时间, 提高了程序的执行效率^[16]. Spark的核心概念是RDD, RDD的一大特性是分布式存储, 每个RDD可以在不同工作节点存储并计算,另一大特性是延迟计算, 一个完整的RDD运行任务被分为Transformation和Action两部分^[17], Transformation创建RDD, 同时提供map、filter、join等大量操作方法生成新的RDD, Action通过执行count、reduce、collect等方法真正执行数据的计算部分.

本文将蚂蚁封装为Ant类, 可行路线的搜索过程实现在Ant类的search()方法中, 实例化 $n$ 个Ant对象生成蚁群, 蚁群间通过ant.set_parameter方法共享参数, 利用Spark的parallelize()方法将蚁群转换为分布式的RDD, 在每轮迭代中通过Spark中的map()方法实现 $n$ 只蚂蚁的并行search()过程, 一轮迭代结束后通过Spark中的collect()方法收集蚁群计算结果, 得到本轮最优结果后统一更新参数, 核心计算过程如图2所示, 从而实现蚁群分布式并行构建可行解, 提升计算效率.

2.5 算法描述

基于Spark的改进蚁群算法对VRPTW的求解流程如图3所示.

具体算法步骤如算法1.

算法1. 基于Spark的改进蚁群算法

(1) 读入算例文件, 初始化车辆数m、车辆容量load, 构造地图(横坐标x、纵坐标y、需求demand、最早开始时间ready、最晚结束时间due、服务时间service_time), 并计算地图上各节点间距离;

(2) 采用最近邻贪心算法获得初始可行解和初始路径长度 ${C_0}$ ;

(3) 实例化参数类, 设置α, β, ρ, τ₀等参数, 基于初始路径长度设置信息素初值τ₀τ_max=1/C₀, 生成全局参数;

(4) 将蚂蚁封装为Ant类, 根据蚂蚁数目实例化数个Ant对象生成蚁群ants, 通过ant.set_parameter方法设置每只蚂蚁的参数, 利用Spark的parallelize(ants)方法将蚁群转换为分布式的RDD;

(5) 在每轮迭代中通过Spark中的map()方法实现n只蚂蚁的并行search()过程, 每只蚂蚁search()方法如下:

① 初始化当前路径road, 加入原点, 设置当前时间current_time=0, 车辆剩余负载remaind_load=load;

② 构造候选节点集, 满足负载、时间窗要求;

③ 从候选节点中依据状态转移规则(10)并采用轮盘赌选择下一个需要服务的节点next并加入当前路径中;

④ 若next节点为空, 将路径加入路径集中, 新派遣一辆车, 置current_time=0, remaind_load=load;

⑤ 判断是否还有未服务的点, 若存在则返回步骤(1), 否则结束

搜索.

(6) 每轮迭代结束后通过Spark中的collect()方法收集蚁群计算结果, 对每只蚂蚁搜索得到的可行解进行排序, 根据图1对迭代最优解进行k-opt局部调整优化;

(7) 得到迭代最优解后通过ant.set_parameter方法统一更新参数, 各路径信息素浓度更新公式参考式(9)、(11)、(12), 采用T^Ibest和T^Gbest轮流进行更新、自适应信息素蒸发策略且限制信息素范围为[τ_min, τ_max];

(8) 判断迭代是否终止, 迭代终止输出全局最优解, 否则返回步骤(4)继续并行化求解.

3 实验设计及结果分析

为测试基于Spark的改进蚁群算法对VRPTW的求解效果, 本文在物理机上利用Virtual Box构建3台虚拟机搭建Spark集群, 并分别在单台虚拟机和Spark集群上进行实验.

3.1 实验环境及算例说明

实验环境如下:

(1) 单机运行环境

操作系统: Ubuntu 16.04.

硬件环境: Virtual Box虚拟机.

　　　　　Intel Core i7.

　　　　　2 GB内存.

(2) Spark集群运行环境

操作系统: Ubuntu 16.04.

硬件环境: Virtual Box虚拟机.

　　　　 Intel Core i7.

　　　　 2 GB内存.

部署方式: Standalone模式.

集群规模: 1台Master, 2台Slave.

实验采用Solomon benchmark和Gehring & Homberger benchmark两个国际通用基准算例库中的数据, 数据集按照影响VRPTW求解的地理数据分布、客户节点数、时间窗松紧程度、车辆载重上限4个因素进行分类, Solomon数据集规模包括25、50、100节点数, 标号为 ${X_1}{X_2}{X_3}{X_4}$ , ${X_1}$ 取值R、C、RC, 分别表示客户节点随机、聚集、混合分布, ${X_2}$ 表示车辆载重, 取值0或1, ${X_3}{X_4}$ 取值一个两位十进制数, 表示时间窗松紧程度, Gehring & Homberge数据集是大规模数据集, 包括200、400、600、800、1000节点数. 数据包含车辆数上限、载重上限、客户位置坐标、客户需求量、时间窗、服务时间 ^[18].

3.2 实验设计及结果分析 3.2.1 信息素矩阵可视化表达

为直观表达蚁群算法求解VRPTW的行为, 选取Solomon-r101的前25节点进行求解并给出信息素矩阵的可视化表达, 信息素含量被转化成灰度值, 颜色越暗的方格所对应的信息素值越高, 在第0、10、100次迭代之后的实验效果如图4.

由图4可以看出, 主对角线的单元格始终为白色, 表示这些单元格的信息素被初始化为0并且永不更新, 其余单元格初始为黑色表示 ${\tau _0} = {\tau _{\max }}$ , 随着迭代过程反复执行, 单元格间的信息素含量差异越来越大, 最后只有少数边含有较高信息素而被选择为全局最优解.

3.2.2 收敛性比较实验

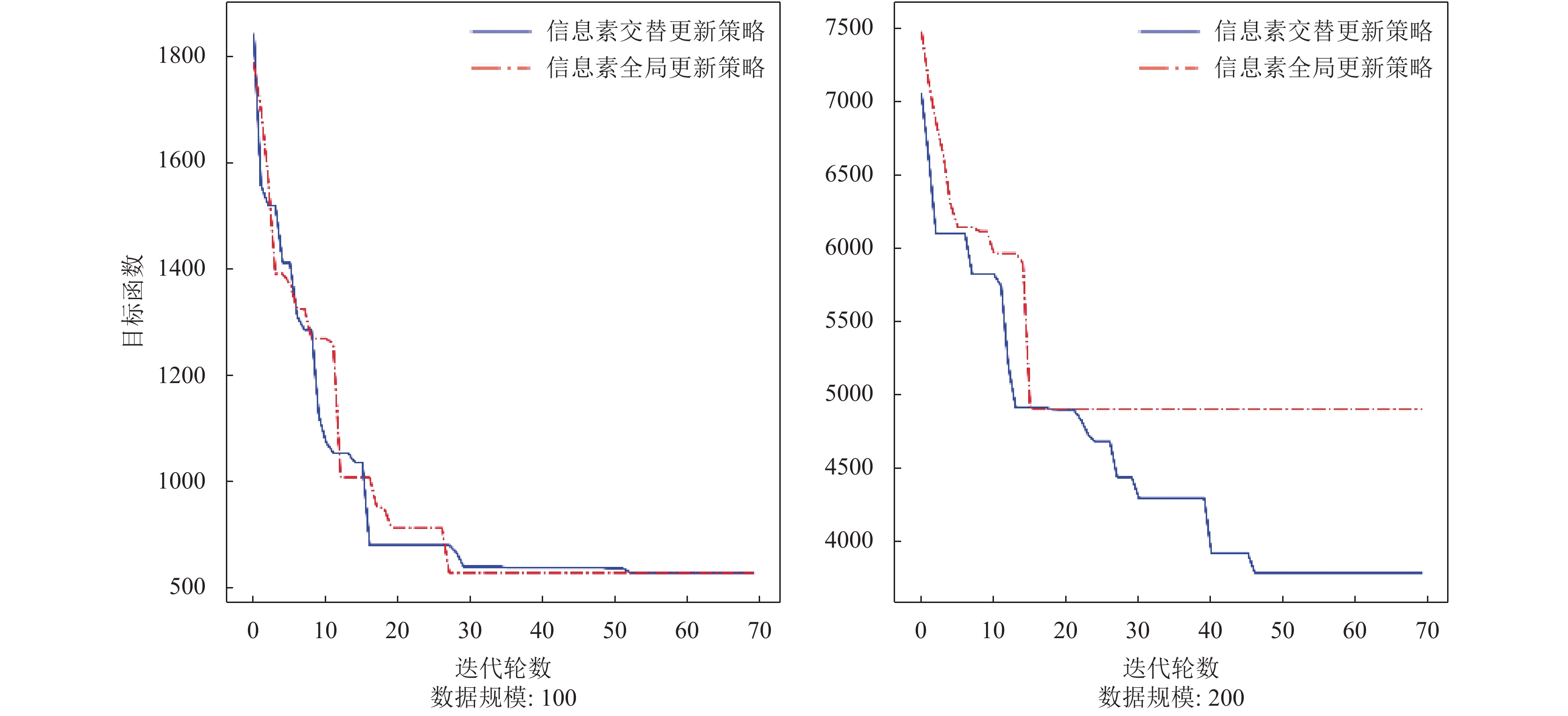
为验证本算法的改进效果, 分别将不同信息素更新策略、不同邻域搜索方法作为控制变量进行实验. 选取Solomon-c101和Gehring & Homberger-c121作为实验数据, 分别采用信息素全局更新和交替更新的求解收敛过程如 图5, 选取Gehring & Homberger-rc121作为实验数据, 分别采用2-opt、3-opt、k-opt这3种邻域搜索的求解收敛过程如图6.

由图5可以看出, 对100节点数据, 信息素更新方式对求解过程无明显影响, 而对200节点数据, 采用全局信息素更新方式使得求解陷入局部最优解而过早收敛, 采用信息素交替更新方式能在执行结束后得到更高质量的解. 由图6可以看出, 使用k-opt进行局部搜索优化比2-opt和3-opt得到的解的精度高. 综上, 改进蚁群算法求解较大规模VRPTW时在迭代初期收敛速度较快, 在迭代中后期能保持全局搜索能力使求解持续收敛, 最终在期望的时间内收敛于一个精度较好的近似解.

3.2.3 求解精度比较实验

为验证本算法的求解精度, 选取Solomon节点数为100的各类数据和Gehring & Homberger benchmark节点数为200及400的大规模各类数据进行测试, 参数设置为: $\alpha = 1$ , $\beta = 2$ , $\rho = 0.9$ , 迭代400轮计算与当前最优解的误差率见表1.

由表1可以看出, 对100以内小规模问题求解的精度基本可达最优解; 对混合分布的RC类问题求解精度有明显提升; 对随机分布的R类问题误差率仍较高, 尤其是对车辆载重小且最大可服务时间短的R1类问题精度更差, 原因是该类问题节点的随机分布增大了路径构造的难度, 各子路线可能包含的节点数差异大; 对200、400节点的大规模问题在计算速度提升的前提下精确度在可接受的误差范围内.

3.2.4 求解速度比较实验

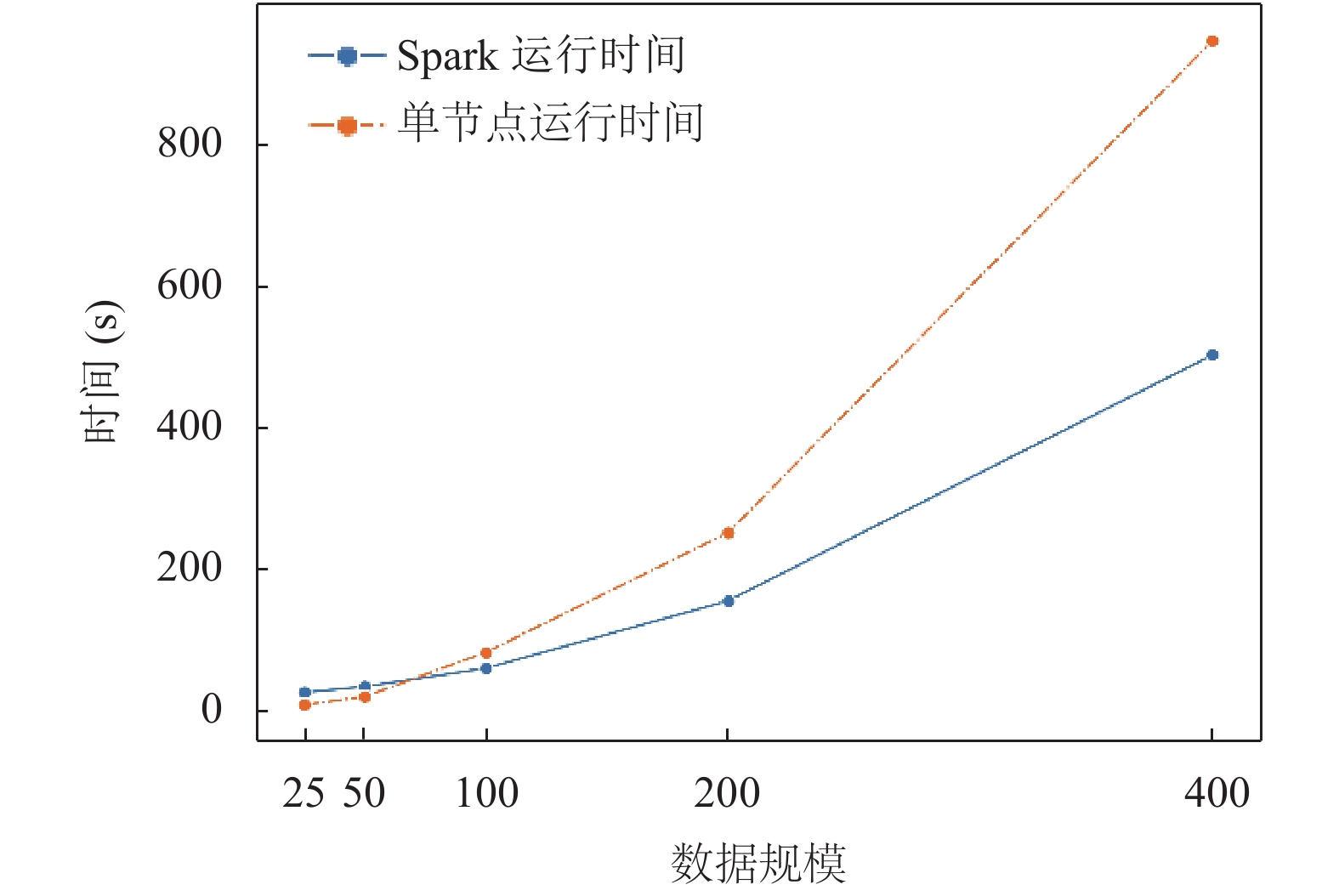
为比较单机求解和基于Spark平台并行求解的求解效率, 选取客户数为25、50、100、200以及400的Solomon-r101、Gehring & Homberge-R1_2_1、Gehring & Homberge-R1_4_1作为实验数据, 基于相同参数和迭代轮数进行实验, 实验结果如 图7.

从图7可以看出, 当问题规模较小时, 由于Spark内部的通信消耗, 基于Spark的并行蚁群算法的求解效率较单机蚁群算法没有显著的提升, 而当问题规模逐步增大时, 基于Spark的并行蚁群算法的求解时间要显著少于单机算法的求解时间, 并行算法的加速比逐步增加, 当客户数为400时, 并行算法的加速比为1.95.

4 总结与展望

本文设计了一种基于Spark的改进蚁群算法求解带时间窗的车辆路径问题, 根据改进的状态转移规则和轮盘赌选择机制构建初始解, 结合k-opt邻域搜索进行局部搜索优化, 采用全局最优解和局部最优解交替更新策略、自适应信息素蒸发策略改进最大最小蚁群算法中的信息素更新策略, 借助Spark计算平台, 将蚁群封装为弹性分布式数据集, 实现蚂蚁的并行搜索.

实验结果表明本算法对100以内小规模问题求解的精度基本可达最优解, 对混合分布的RC类问题求解精度有提升, 对200、400节点的大规模问题求解效率有明显提升. 因此把蚁群算法这样的启发式算法和邻域搜索相结合是解决优化问题的有效途径, 另外利用Spark分布式平台处理蚁群算法中耗时的迭代过程可以有效降低计算时间.

本文试图对C、R、RC类VRPTW问题同时取得较好的优化效果, 但对R类分布的节点求解精度还不理想, 今后可结合其它群体智能算法或者根据随机分布类问题的特点进行合适的参数调整对R类VRPTW问题进行进一步优化求解. 另外本文尚未对600、800、1000等更大规模节点进行实验, 今后可以通过改进算法、充分利用分布式平台、提升硬件环境来解决更复杂的大规模求解问题.