空间信息技术是自20世纪60年代以来逐渐发展起来的信息技术的总称, 用于获取, 管理和分析与地理位置相关的空间信息[1]. 它以人类的生活环境为主要研究对象, 以遥感(Remote Sensing, RS)、全球定位系统GPS(Global Position System)和地理信息系统(Geographic Information System, GIS)技术为代表, 它不仅是客观数据的集合, 而且是从收集、处理、测量和分析到地理空间数据和信息的管理、存储、显示和发布的整个信息流程. 它具有客观获取、准确定位、灵活管理、空间分析和视觉表达的特点[1].
在空间数据中, 具有不均匀位置分布的数据被称为离散数据, 在平面二维地理空间的定位中, 离散数据的坐标由不规则分布的离散样本的平面坐标实现. 高程和属性值通常用作第三维数据. 空间插值则是一种通过这些离散的空间数据计算未知空间数据的方法. 它是基于“地理学第一定律”的基本假设: 空间位置上越靠近的点, 具有相似特征值的可能性越大, 而距离远的点, 其具有相似特征值的可能性越小[2]. 它通常用于将离散点的测量数据转换为连续数据表面, 以便于比较其他空间现象的分布情况.
空间插值分析算法的分类方式有多种: 按插值的区域范围分类, 可以分为整体插值、局部插值、边界内插法等[3]; 整体插值是用研究区的所有采样点进行全区特征拟合, 在整体插值方法中, 整个区域的数值会影响单个插值点的数值, 同样单个采样点的数值的增加、减少或删除对整个区域的特征拟合都有影响[3], 代表性插值方法具有趋势面分析插值方法等. 局部插值是使用相邻数据点来估计未知点的值, 首先定义邻域或搜索范围, 然后搜索属于该区域的数据点, 然后选择可以表示此有限点空间变化的数学函数, 最后通过计算为该邻域或者该区域内的未知点赋值[3], 代表插值方法有样条函数插值法[4]、反距离权重插值法[5]、Kriging插值法[6]等. 边界内插规则假设值和属性的任何变化发生在特定区域的边界线上, 并且边界内属性的变化是均匀和同质的, 主要的插值法是泰森多边形法.
按照插值的标准分类, 可以分为确定性插值、地统计插值. 确定性插值法主要采用数学工具, 利用函数的方法来进行插值, 这种方式用来研究某区域内部的相似性, 其代表插值法有反距离加权插值法[7]等; 地统计插值是基于空间自相关性的, 由观测数据产生具有统计关系的曲面, 代表插值法是Kriging插值法[7].
按插值的精度分类, 可以划分为精确插值、近似插值. 精确插值生成包括所有观测点的曲面, 而近似插值生成不包含所有观测点曲面[8].
随着生产、研究应用的不断深入, 越来越多的插值算法被提出和不断改进. 本文将对适用性高、性能卓越、应用场景广泛的泰森多边形法、反距离权重插值法、样条函数插值法与克里金插值法进行研究综述, 并对空间插值算法的未来的研究方向进行展望.
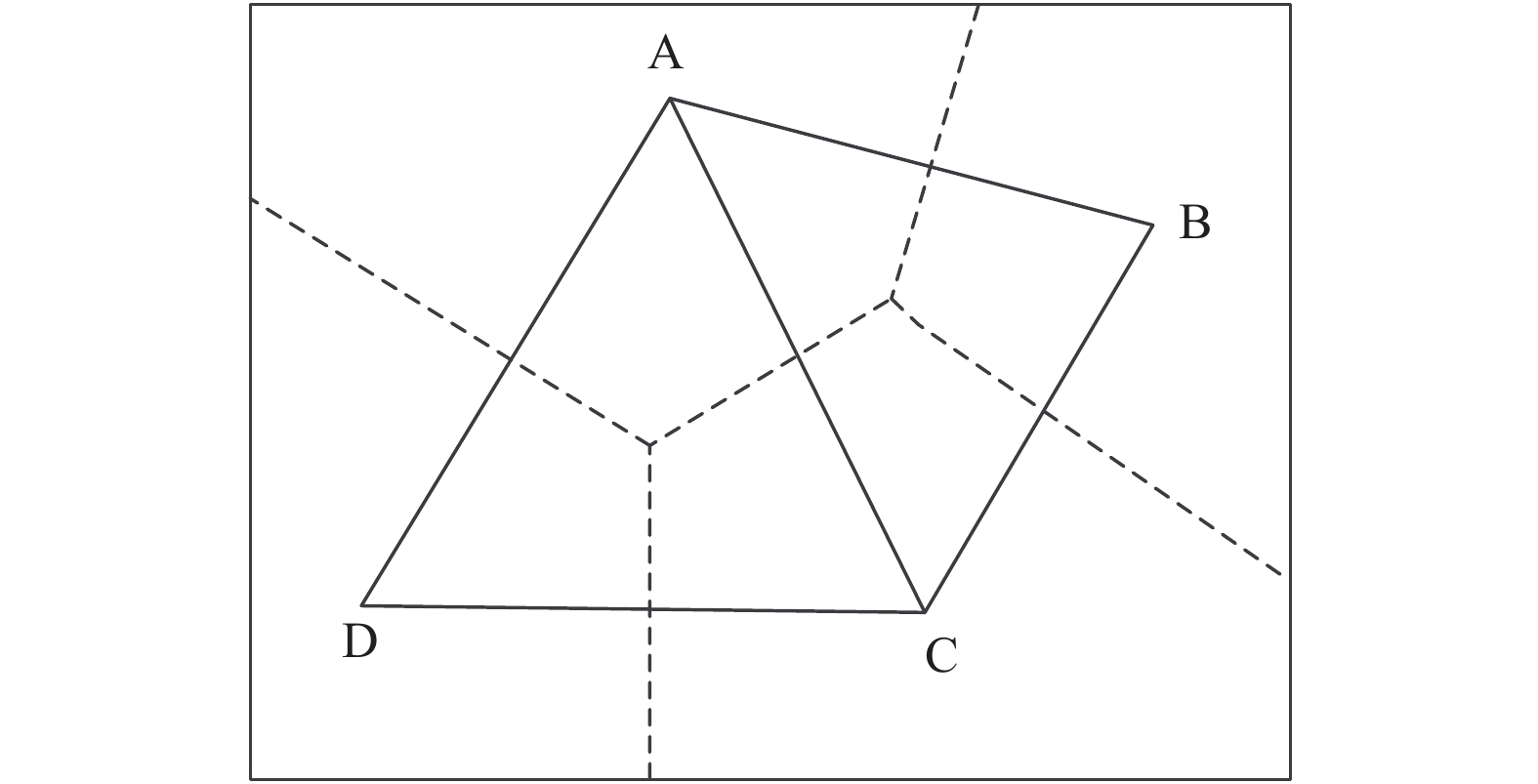
1 泰森(Thiessen)多边形荷兰气候学家Thiessen AH提出泰森(Thiessen)多边形法, 根据离散分布的气象站的降雨量来计算平均降雨量, 所有相邻气象站以三角形连接, 在三角形的每一边作垂直平分线, 因此气象站周围有几个垂直平分线包围的多边形[8]. 用某多边形内所包含的单独的气象站的降雨强度来表示该多边形区域内的降雨强度, 该多边形称为泰森多边形. 如图1所示, 图中虚线形成的多边形就是泰森多边形, A、B、C、D分别为离散观测点, 一个泰森多边形内仅包含一个离散观测点, 泰森多边形的每个顶点都是每个三角形的外接圆心[1]. 泰森多边形也被称为Voronoi图或dirichlet图[3].
|
图 1 泰森多边形示意图 |
泰森多边形利用离散观测点的值对该点所在的区域进行赋值, 得到的结果往往是数值的变化只发生在多边形的边界上, 而多边形内部的数值则是均匀、同质的[9]. 其数学表达式为:
| ${V_e} = {V_i}$ | (1) |
其中, Ve表示待插值点的距离, Vi表示i示点的离散观测值. i点必须满足如下条件:
| ${d_{ei}} = \min ({d_{e1}},{d_{e2}}, \cdots, {d_{en}})$ | (2) |
其中, dij表示点i(xi,yi) 与点j(xj,yj)间的欧几里德距离[8].
泰森多边形的关键是将离散观测点合理地连接到三角网络中, 即构造Delaunay三角网络[3]. 构建泰森多边形步骤如图2所示.

|
图 2 泰森多边形创建流程 |
泰森多边形反映了离散观测点的空间控制范围或者是势力范围, 它适用于较小区域内、空间变异性不高的情况, 距离近的点比距离远的点更相似, 比较符合人的逻辑思维[10]. 同时, 它的实现不需要其他前提条件, 效率高, 方法简单, 但是受样本观测值的影响较大, 没有考虑空间因素、变量以及其他某些规律, 只考虑距离因素, 实际效果不是很理想.
泰森多边形插值法也在进行不断改进发展, 其中自然邻域法就是改进的一种, 它的基本原理是在插值点创建一个新的多边形, 新多边形与原始多边形的重叠比例作为观测点数值的权重, 通过这种方式计算插值点的估计值[7]. 另外, 刘金雅等人将泰森多边形与最小累计阻力模型相结合[11], 用于估算京津冀城市群生态系统服务价值; 祁春阳等人将泰森多边形与虚拟力算法、质心算法相结合, 提出VFVP算法策略来提高无线传感网络覆盖率[12]; 戚远航等人提出了一种基于泰森多边形的离散蝙蝠算法来解决多车场车辆路径问题[13]; 罗浩将泰森多边形应用于人脸区域分割进行关键特征提取来实现人脸识别的新算法[14].
泰森多边形适用于样本点分布均匀的较小区域内空间变异性不明显的场景, 允许少量的数据缺失, 它可应用于气象降水、无线网络规划、计算机视觉等领域的定性分析、统计分析以及邻近分析中, 泰森多边形算法正在更广阔的应用于空间区域相关的新领域.
2 反距离权重插值(IDW)反距离权重插值法[15]最初是由Shepard提出, 后来经过持续不断的改进发展. 它的最重要的一个假设就是观测点对于插值点都会有局部影响, 任意一个观测点的值对插值点值的影响都是随着距离的不断增加而不断减弱的[16], 在估计插值点的值时, 假设距离估计插值点最近的N个观测点对该插值点有影响, 则这N个观测点对插值点的影响与它们之间的距离成反比关系[17]. 因此更接近插值点的观测点将被赋予的权重更大, 而且权重的和为1.
IDW的数学表达式:
| ${\hat Z_0} = \sum\limits_{i = 0}^n {\left( {{Z_i}{Q_i}} \right)} $ | (3) |
其中,
权重系数Qi的计算是反距离加权算法的关键, 通常由下式给出:
| ${Q_i} = \frac{{f({d_{ej}})}}{{\sum\limits_{j = 1}^n {f({d_{ej}})} }}$ | (4) |
其中, n是已知观测点的数量, f(dej)表示已知观测点与插值点之间已知距离dej的权重函数, 最常用的一种形式是:
| $f({d_{ej}}) = \frac{1}{{d_{ej}^b}}$ | (5) |
其中, b是合适的常数. 当b取值为1或2时, 此时是反距离倒数插值和反距离倒数平方插值[17].
反距离权重插值作为一种全局插值算法, 它的所有离散观测点都将参与每一插值点数值的计算, 同时, 它也是一种精准插值, 插值生成的曲面中的预测的观测值与实测的观测值完全一致. 它综合了基于泰森多边形的自然邻域法和多元回归渐变方法的有点, 不仅考虑了距离因子, 还为邻近插值点的离散观测点根据距离分配权重, 当出现各向异性时, 还会考虑方向的权重. 距离权重函数与从插值点到观测点的距离次幂成反比, 随着观测点与插值点之间距离的不断扩大, 权重呈现幂函数递减趋势[19]. 如表1所示.
| 表 1 反距离权重插值与相关方法的比较 |
IDW简便易操作, 不会出现无法解释的无意义结果, 即使观测点数据集的变化波动很大也能够得到一个比较合理的结果[17]. 但是, IDW对权重函数的选择特别敏感, 权重函数存在细微差别对生成的结果会有较大的波动, 而且易受观测点数据集的影响, 由于数据集的影响, 可能存在孤立的分布模式, 其中部分点数据高于其他周围数据.
反距离权重算法的应用不断发展, 李正泉对IDW进行优化改进, 在传统IDW算法的基础上添加用于反映样点方位的调和权重系数K, 来减小或者克服样点方位分布不均的问题[21]; 王家润提出了IDW并行优化的线程任务分解模型[22], 提升了硬件加速能力, 降低了并行编程任务划分难度; 刘玮将IDW模型应用于鼠尾藻群体数量分布的计算且能够反映鼠尾藻群体的空间分布[23].
反距离权重插值适用于表现出均匀分布而且足够密集以反映局部差异的观测点数据集的场景, 提供合理的插值结果, 它普遍适用于空气质量、气象、土壤等领域的研究, 尤其适用于当某个现象呈现出局部变异性的情况.
3 样条函数插值(Spline)样条函数S(x)是一个分段函数, 在区间[a, b]是一个连续可微的函数, 如图3所示.
给定一组节点:
| $a = {x_0} < {x_1} < \cdots < {x_n} = b$ | (6) |
其中, S(x)满足在每个子区间[xi, xi+1](n=0, 1, 2, …, n–1)上是次数不超过m的多项式且在区间上有m–1阶连续导数, 则称S(x)是定义在[a, b]上的m次样条函数[24].
样条函数插值的目标是找到满足最佳平滑原理的曲面, 并使用样本观察点以最小化曲面曲率拟合平滑曲线[25]. 使用最小化表面总曲率的数学函数来估计插值点的值, 从而在输入点之后生成平滑表面. 其表达式:
| ${\hat Z_0} = T\left( {x,y} \right) + \sum\limits_{i = 0}^n {{\lambda _i}R{{\left( {{r_i}} \right)}_{}}} $ | (7) |
其中,
样条函数主要划分为规则样条函数和张力样条函数[4], 两类函数对比如表2所示.
对于规则样条函数, R(ri)和T(x, y)表达式如下:
| $T\left( {x,y} \right) = {a_1} + {a_2}x + {a_3}y$ | (8) |
| $R\left( {{r_i}} \right) = \dfrac{{\dfrac{{r_i^2}}{4}\left[ {\ln \left( {\dfrac{{{r_i}}}{{2\Pi }}} \right) + c - 1} \right] + {\tau ^2}\left[ {{k_0}\left( {\dfrac{{{r_i}}}{\tau }} \right) + c + \ln \left( {\dfrac{{{r_i}}}{{2\Pi }}} \right)} \right]}}{{2\Pi }}$ | (9) |
其中, c是实常数, a是线性方程系数,
对于张力样条函数, R(ri)和T(x,y)表达式如下:
| $T\left( {x,y} \right) = {a_1}$ | (10) |
| $R\left( {{r_i}} \right) = \frac{1}{{2\Pi {\phi ^2}}}\left[ {\ln \left( {\frac{{r\phi }}{2}} \right) + c + {k_0}\left( {r\phi } \right)} \right]$ | (11) |
其中, c为常数, a为线性方程系数,

|
图 3 样条函数示意 |
| 表 2 两类样条函数的比较 |
样条函数插值不断改进发展, 张海燕利用三次样条函数进行GNSS高程拟合[26], 具有很好的适应性; 高茂庭提出了一种基于遗传算法的B样条拟合算法[27], 有效提高了精度并加快了收敛速度; 胡蓉利用多亲遗传算法对B样条函数进行优化[28], 实现玻璃搬运机器人轨迹的优化.
样条函数插值速度快, 且产生的视觉效果好, 但样条函数插值的误差不能直接计算, 适用于属性值在短距离内变化不大的区域范围, 它广泛应用于测绘、统计学、计算几何等领域.
4 克里金(Kriging)插值算法克里金插值算法也称为空间自协方差最佳插值法[29], 它是以南非矿业工程师Krige DG的名字命名的一种最优内插法[30], 以变异函数理论和结构分析为基础[31], 适用于区域化变量存在空间相关性, 假设都是空间相关性且所有随机误差都具有二阶平稳性. 其表达式:
| ${\hat Z_0} = \sum\limits_{i = 0}^n {{\lambda _i}{Z_i}} $ | (12) |
其中,
这样来看, 插值点值的好坏完全取决于
当Zi的E(Zi)=m已知, 则将这种克里金插值法成为简单克里金插值法[33], 此时简单克里金的表达式为:
| ${\hat Z_0} = \sum\limits_{i = 0}^n {{\lambda _i}{Z_i} + m\left( {1 - \sum\limits_{i = 1}^n {{\lambda _i}} } \right)} $ | (13) |
简单克里金插值法的插值点的精度在很大程度上取决于m值的大小.
当Zi的E(Zi)为未知常数, 则将这种克里金插值法成为普通克里金插值法[33], 求解权重系数的表达式为:
| $\left\{ \begin{array}{l} \displaystyle\sum\limits_{i = 1}^n {{\lambda _i}Cov\left( {{x_i},{x_j}} \right) - \mu = Cov\left( {{x_0},{x_i}} \right)} \\ \displaystyle\sum\limits_{i = 1}^n {{\lambda _i} = 1} \\ \end{array} \right.$ | (14) |
以上方程组中,
| $\gamma \left( {{x_i},{x_j}} \right) = \frac{1}{2}E{\left[ {Z\left( {{x_i}} \right) - Z\left( {{x_j}} \right)} \right]^2}$ | (15) |
当Zi的E(Zi)=m(xi)时, 即在插值区域内是非平稳的, 协方差或变异函数已知, 此时被称为泛克里金插值法[35], m(xi)就是在这xi的期望值, 即漂移. 泛克里金插值法是一种地统计学方法, 它考虑到了有漂移的无偏线性估计量[34]. 泛克里金插值方法求解权重系数的方程组的表达式:
| $\left\{ \begin{array}{l} \displaystyle\sum\limits_{i = 1}^n {{\lambda _i}Cov\left( {{x_i},{x_j}} \right) - \sum\limits_{}^{} {{\mu _l}{f_l}\left( {{x_i}} \right)} = Cov\left( {{x_0},{x_i}} \right)} \\ \displaystyle\sum\limits_{i = 1}^n {{\lambda _i}{f_l}\left( {{x_i}} \right) = {f_l}\left( x \right)} \\ \end{array} \right.$ | (16) |
当研究某一阈值特异值时需要一种非参数地统计学方法, 称之为指示克里金插值法[34], 对于某一区域观测值, 任意指定已阈值z, 引入指示函数l(x,z), 表达式如下:
| $l\left( {x,z} \right) = \left\{ \begin{gathered} 1,\;\;\;Z\left( {{x_i}} \right) \leqslant z \\ 0,\;\;\;Z\left( {{x_i}} \right) > z \\ \end{gathered} \right.$ | (17) |
其变异函数表达式:
| $\gamma \left( {{x_i},{x_j}} \right) = \frac{1}{{2N}}\sum\limits_{i = 0}^N {{{\left[ {l\left( {{x_i},z} \right) - l\left( {{x_j},z} \right)} \right]}^2}} $ | (18) |
当已知任意区域二维概率分布时, 对插值点的估计值的一种非线性地统计法称之为析取克里金插值[36], 它是一种非线性、最小方差的无偏估计方法, 其表达式:
| ${\hat Z_0} = \sum\limits_{i = 0}^n {{f_i}\left( {{Z_i}} \right)} $ | (19) |
其中, fi(Zi)为未确定函数, 根据Hermiet多项式的正交性用于拟合法向变形函数以估计插值点的值.
当利用多个区域变量之间的互相关性, 通过建立模型用观测点的数据值对插值点数据值进行估计, 被称为协同克里金插值[37], 这是一种多变量地统计学研究的基本方法, 是基于协同区域化变量理论. 协同区域化是指定义在同一空间域, 并且在统计及空间位置上具有一定程度相关性的区域化变量. 协同克里金插值表达式:
| ${\hat Z_0} = \sum\limits_{k = 1}^K {\sum\limits_{{i_k} = 0}^{{n_k}} {{\lambda _{{i_k}}}{Z_{{i_k}}}} } $ | (20) |
从表达式可以看出, 协同克里金插值的估计量是K个协同区域化变量的所有有效值的线性组合.
多种克里金插值法的比较如表3所示.
| 表 3 多种克里金插值法的比较 |
克里金插值法也在不断的发展, 陈光使用NM单纯形算法对克里金变异函数模型进行改进优化[38], 提高无线传感器网络的性能; 顾军华利用VIRE算法和克里金插值实现室内的精确定位[39]; 邓岳川采用克里金插值法从空间分布的角度提出构建多路径误差的模型, 实现对指定测区内的多路径误差的空间分布特征的探究[40].
克里金插值算法适用于样本数据存在随机性和结构性特征的场景, 广泛应用于各类观测的空间插值, 地面风场、降雨、土壤、环境污染等领域.
结合上述空间插值算法的原理及应用, 总结了这些算法的逼近程度、处理速度、推算能力以及适应范围[41], 使用分值1~5表示由弱到强, 对比结果如表4所示.
| 表 4 空间插值算法对比 |
5 结论
本文综述了一系列的空间插值分析算法的插值原理和应用, 经过几十年的不断发展, 空间插值算法不断完善, 并逐渐趋于成熟, 不断被应用到土壤水质、海洋环境、地质勘探、空气质量等诸多领域. 虽然空间插值算法的应用领域广阔, 但是依然存在一些问题, 空间插值算法未来的发展应当需要根据不同的应用场景不断的进行研究优化与完善, 不断形成更加符合真实场景的空间插值算法.
首先, 随着空间插值分析算法的不断发展以及机器学习的不断发展, 王辉赞等提出了支持向量机的克里金插值算法的在海洋数据方面的实验[42], 邱云翔提出的粒子群优化BP神经网络在降雨空间插值的应用[43], 程家昌等人利用BP神经网络插值方法对研究区土壤的氮和磷进行空间插值预测, 比传统插值算法具有更强的的泛化能力[44], 李纯斌等人以BP神经网络和支持向量机模型为研究对象, 构建降水量空间插值模型[45], 大量的关于空间插值算法的新的探索已经广泛展开, 并在降雨降水、土壤勘测、海洋资料等应用邻域取得了一定成果. 未来可继续在机器学习以及人工智能等方面促进空间插值算法的进一步研究.
其次, 空间插值分析算法的不再是紧紧局限于传统意义上的地理信息系统, 国内外的研究者将空间插值的思想特性引入各行各业, 体现着空间插值分析算法的作用与意义. 未来可以在空间插值分析算法应用的各个方面不断加深算法的适应性改进.
最后, 所需要解决的实际问题大多都是离散型问题, 空间插值分析算法需要根据实际情况进行建模分析、具体设计, 然而算法的改进并不能保证获得最好的结果, 怎样改进空间插值分析算法能够获得更优更合理的结果都需要进行深入的研究与探讨.
| [1] |
王玉璟. 空间插值算法的研究及其在空气质量监测中的应用[硕士学位论文]. 开封: 河南大学, 2010. 1–3.
|
| [2] |
朱阿兴, 杨琳, 樊乃卿, 等. 数字土壤制图研究综述与展望. 地理科学进展, 2018, 37(1): 66-78. |
| [3] |
崔清松. 空间插值算法在地质建模中的应用[硕士学位论文]. 南充: 西南石油大学, 2010.
|
| [4] |
李俊龙, 丁页, 刘喜惠, 等. 全国近岸海域水质空间插值算法精度分析. 中国环境监测, 2015, 31(2): 135-140. DOI:10.3969/j.issn.1002-6002.2015.02.027 |
| [5] |
任志勇. 辽宁省某市降雨量的空间插值算法比较研究. 北京测绘, 2017, 31(5): 164-166. |
| [6] |
孔令娜, 向南平. 基于ARCGIS的降水量空间插值方法研究. 测绘与空间地理信息, 2012, 35(3): 123-126. DOI:10.3969/j.issn.1672-5867.2012.03.038 |
| [7] |
董志南, 郑拴宁, 赵会兵, 等. 基于空间插值的风场模拟方法比较分析. 地球信息科学学报, 2015, 17(1): 37-44. |
| [8] |
王丽娜. 气象要素空间插值算法的研究及其应用[硕士学位论文]. 重庆: 重庆理工大学, 2014.
|
| [9] |
Gao J, Revesz P. Voting prediction using new spatiotemporal interpolation methods. Proeeedings of 2006 Intenational Conference on Digital Government Research. San Diego, CA, USA. 2006. 293–300.
|
| [10] |
刘鑫, 魏占民, 刘虎, 等. 基于GIS和Thiessen多边形的区域土壤类型分布图制图方法. 中国农村水利水电, 2011(10): 141-145. |
| [11] |
刘金雅, 汪东川, 张利辉, 等. 基于多边界改进的京津冀城市群生态系统服务价值估算. 生态学报, 2018, 38(12): 4192-4204. |
| [12] |
祁春阳, 戴欢, 赵晓燕, 等. 基于虚拟力和泰森多边形的分布式覆盖算法. 计算机工程与设计, 2018, 39(3): 606-611. |
| [13] |
戚远航, 蔡延光, 蔡颢, 等. 泰森多边形的离散蝙蝠算法求解多车场车辆路径问题. 控制理论与应用, 2018, 35(8): 1142-1150. |
| [14] |
罗浩. 基于特征分割的人脸识别算法与实现[硕士学位论文]. 武汉: 武汉科技大学, 2018.
|
| [15] |
Daly C. Guidelines for assessing the suitability of spatial climate data sets. International Journal of Climatology, 2006, 26(6): 707-721. DOI:10.1002/(ISSN)1097-0088 |
| [16] |
高真, 叶学义, 周天琪, 等. 基于反距离加权插值的水声数据可视化算法. 计算机工程, 2015, 41(9): 266-270, 275. |
| [17] |
张锦明, 郭丽萍, 张小丹. 反距离加权插值算法中插值参数对DEM插值误差的影响. 测绘科学技术学报, 2012, 29(1): 51-56. DOI:10.3969/j.issn.1673-6338.2012.01.013 |
| [18] |
余小东, 武莹, 何腊梅. 反距离加权网格化插值算法的改进及比较. 工程地球物理学报, 2013, 10(6): 900-904. |
| [19] |
Lu GY, Wong DW. An adaptive inverse-distance weighting spatial interpolation technique. Computers & Geosciences, 2008, 34(9): 1044-1055. |
| [20] |
陈许霞, 季民, 宁方志. 基于GIS的格点精细化预报插值方法的研究. 测绘与空间地理信息, 2016, 39(10): 69-71, 74, 78. DOI:10.3969/j.issn.1672-5867.2016.10.020 |
| [21] |
Li ZQ, Wu YX. Inverse distance weighted interpolation involving position shading. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 91-98. |
| [22] |
王家润, 谢海峰. 基于任务分解模型的离散数据格网化并行优化. 计算机工程与设计, 2018, 39(6): 1774-1781. |
| [23] |
刘玮, 辛美丽, 吕芳, 等. 关于鼠尾藻群体数量分布的三种统计模型比较. 生态学报, 2018, 38(6): 2031-2040. |
| [24] |
陈浩, 华灯鑫, 张毅坤, 等. 基于三次样条函数的激光雷达数据可视化插值法. 仪器仪表学报, 2013, 34(4): 831-837. DOI:10.3969/j.issn.0254-3087.2013.04.018 |
| [25] |
葛莹, 徐旭, 路新强, 等. 引入各向异性的规则张力样条函数插值. 测绘科学, 2013, 38(6): 137-139. |
| [26] |
张海燕, 李秀海, 韩冰. 基于三次样条函数的长线路GNSS高程拟合研究. 测绘工程, 2018, 27(7): 15-17, 23. |
| [27] |
高茂庭, 冯莉. 基于遗传算法的B样条曲线拟合改进算法. 计算机应用研究, 2019, 36(10): 预发表.
|
| [28] |
胡蓉. 一种玻璃搬运机器人轨迹规划和优化研究. 机械设计与制造, 2018(9): 164-167. DOI:10.3969/j.issn.1001-3997.2018.09.044 |
| [29] |
Nalder IA, Wein RW. Spatial interpolation of climatic normals: Test of a new method in the Canadian boreal forest. Agricultural and Forest Meteorology, 1998, 92(4): 211-225. DOI:10.1016/S0168-1923(98)00102-6 |
| [30] |
Kidner DB. Higher-order interpolation of regular grid digital elevation models. International Journal of Remote Sensing, 2003, 24(14): 2981-2987. DOI:10.1080/0143116031000086835 |
| [31] |
Marinoni O. Improving geological models using a combined ordinary-indicator Kriging approach. Engineering Geology, 2003, 69(1–2): 37-45. |
| [32] |
史文娇, 岳天祥, 石晓丽, 等. 土壤连续属性空间插值方法及其精度的研究进展. 自然资源学报, 2012, 27(1): 163-175. |
| [33] |
颜慧敏. 空间插值技术的开发与实现[硕士学位论文]. 南充: 西南石油学院, 2005.
|
| [34] |
李晓军, 张振远. 基于指示和普通克里金的不连续地层厚度估计方法. 岩石力学, 2017, 35(10): 2881-2887. |
| [35] |
牛文杰, 朱大培, 陈其明. 泛克里金插值法的研究. 计算机工程与应用, 2001, 37(13): 73-75, 99. DOI:10.3321/j.issn:1002-8331.2001.13.025 |
| [36] |
马先林, 周坤瑞. 析取克里金技术在油藏描述中的应用. 石油大学学报(自然科学版), 1992, 16(3): 116-121. |
| [37] |
胡丹桂, 舒红. 基于协同克里金空气湿度空间插值研究. 湖北农业科学, 2014, 53(9): 2045-2049. DOI:10.3969/j.issn.0439-8114.2014.09.018 |
| [38] |
陈光. 基于改进克里金算法的WSNs环境监测方法研究[硕士学位论文]. 南京: 南京邮电大学, 2017.
|
| [39] |
顾军华, 许鹏, 董瑶, 等. 基于克里金插值的自适应VIRE室内定位算法研究. 计算机工程与应用, 2018, 54(12): 100-104. DOI:10.3778/j.issn.1002-8331.1709-0242 |
| [40] |
邓岳川, 谷双喜. 克里金插值的多路径误差空间分布特征. 测绘科学, 2018, 43(4): 17-23. |
| [41] |
刘光孟, 汪云甲, 张海荣, 等. 空间分析中几种插值方法的比较研究. 地理信息世界, 2011, 9(3): 41-45. DOI:10.3969/j.issn.1672-1586.2011.03.008 |
| [42] |
王辉赞, 张韧, 刘巍, 等. 支持向量机优化的克里金插值算法及其海洋资料对比试验. 大气科学学报, 2011, 34(5): 567-573. DOI:10.3969/j.issn.1674-7097.2011.05.006 |
| [43] |
邱云翔, 张潇潇, 刘国东. 粒子群算法优化BP在降雨空间插值中的应用. 长江科学院院报, 2017, 34(12): 28-32. DOI:10.11988/ckyyb.20160837 |
| [44] |
程家昌, 黄鹏, 熊昌盛, 等. 基于BP神经网络的土壤养分空间插值. 广东农业科学, 2013, 40(7): 64-67, 71. DOI:10.3969/j.issn.1004-874X.2013.07.020 |
| [45] |
李纯斌, 刘永峰, 吴静, 等. 基于BP神经网络和支持向量机的降水量空间插值对比研究——以甘肃省为例. 草原与草坪, 2018, 38(4): 12-19. DOI:10.3969/j.issn.1009-5500.2018.04.002 |
 2019, Vol. 28
2019, Vol. 28



