板球系统是一个欠约束、强耦合的控制系统, 通过对球的位置的检测、跟踪、定位, 从而控制小球运动. 无论是对小球位置的识别还是控制小球运动都可以应用到实际的工程中. 通过对小球识别方式的不同主要可以分为基于视觉、基于光电晶体管以及基于触摸屏[1]的板球系统. 近今年来计算机视觉飞速发展, 从早先的车牌号识别到如今的刷脸识别、行人闯红灯提示, 计算机视觉技术被应用到越来越多的地方, 手机、旅游景点、以及安检等场所. 基于视觉的板球系统研究有机的将计算机视觉与控制理论结合起来, 因此对移动小球的研究具有重要的应用价值. 小球的追踪主要采用摄像头采集图像, 通过图像识别来追踪小球. 特征提取在机器视觉当中占据重要位置, 大量应用在目标检测、目标识别等领域[2]. 目前使用较多的移动目标跟踪方法有: 基于区域匹配相关的跟踪方法; 基于对比度的跟踪方法; 基于变形模板的跟踪方法以及基于光流的追踪方法[3]等. 直方图投影是基于区域匹配相关的跟踪方法[4], 该方法利用概率进行模板匹配, 首先获得匹配模板的图像直方图, 然后对需要追踪的图像进行归一化处理, 得到若干个小的与模板尺寸相等的图像并且得到这些直方图, 与模板直方图进行比较选取最为相似的确定为被最终目标. 基于峰值的对比度跟踪方法[5]是选取图片中最亮的点(既图像函数的峰值点)以及最暗的点(图像函数经倒向相后的峰值点)分别为白目标、黑目标, 然后将其作为参考点进行追踪的方法, 也称峰值追踪. 变形模板的跟踪方法[6]与模板匹配方法相似, 但不同的是模板为含有纹理的面板, 每条纹理通过x方向及y方向变形逐渐与图像中的真实目标相适应, 从而检索出复杂背景下的目标.
本文主要研究内容是基于LK光流法的改进, 在假设亮度不变的情况下[7], 通过亮度相同这个条件在视频流中找到与前一帧亮度相同的特征点, 在追踪的过程中会得到运动场景中特征点的运动方向和运动速度等重要信息, 而特征点的运动方向和运动速度则构成了光流法的核心光流场.
近几年的研究中光流的计算方法主要有以下几种方法: 微分法, 匹配法、基于能量的方法、基于相位的方法、神经动力学方法等[8,9]. 移动目标追踪实时性要求高, 然而稠密光流计算需要对空间所有的像素点进行微分计算, 计算量异常的大, 属于计算密集型的算法, 难以确保其实时性. 在此基础上稀疏光流应运而生, 只需求取其特征点, 再对其特征点进行追踪, 因此大幅度减少了计算量, 实时性得到的有效的提高, 典型代表为LK法[10].
对于板球系统, 传统的LK光流法追踪小球的运动需提取小球的特征, 但颜色单一小球内部灰度梯度变化不大, 特征点通常为小球的边缘位置, 难以自动捕捉到圆心, 造成圆心位置计算出现误差. 因此本文对传统的LK光流法进行改造, 应用霍夫变换[11]提取圆心位置, 对确定的圆心计算灰度梯度使用LK光流法进行追踪, 提高了LK光流法追踪小球圆心的准确性. 同时在对圆的识别中也可以采用传统的直方图变换来进行, 对这两种方法在板球系统中对于小球的识别性能作出比较, 确定改进LK光流法更为适用板球系统中移动小球的捕捉.
1 基于Hough变换的改进光流法本文以反向直方图投影法、LK光流法作为该方法的对照方法. 反向直方图投影法首先计算需要追踪目标模板的直方图, 其次将记录的图像进行归一化, 分割为无数个小图像并计算每一个小图像的直方图, 最终比对模板直方图与小图像的直方图, 其中与模板直方图最为相似的直方图所属是小图像即为需要追踪的目标.
LK光流法是利用人眼观察运动物体时, 物体的影像会在视网膜上形成一系列连续变化的图像, 这一系列连续变化的图像平面信息不断“流过”视网膜, 好像一种光的“流”[12]. 光流法研究的是像素运动的瞬时速度, 其原理是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系, 从而计算出相邻帧之间物体的运动信息的一种方法.
尽管采用传统的LK光流法可以对小球进行追踪且相对稳定, 但是该方法通常只能捕捉灰度梯度大的地方作为角点, 通常为物体轮廓边缘, 很难捕捉出圆心. 同时LK法属于在线追踪, 每一张图片的追踪角点信息都是参照上一帧图片, 如果上一帧角点信息丢失, 则会选取新的角点, 所以无法保证参考角点位置和数量的固定. 如图1所示, (a)、(b)两图为小球的同一运动过程, 小球先经过图(a)位置1随后经过图(b)位置2, 由于LK法属于在线追踪, 图(a)和图(b)的角点位置不能完全重合, 数量也不对等.

|
图 1 LK光流法追踪小球角点位置和数量 |
因此本文对传统LK光流进行改进, 引入霍夫圆变换来方便确定小球中心, 使角点自动确定为圆心, 再进行光流法进行追踪. 为保证追踪效果, 每间隔一段时间会再次调用霍夫变换对圆心进行矫正, 提升LK光流法在复杂背景下对小球圆心捕捉的准确性.
1.1 霍夫圆变换原理霍夫圆变换的基本原理可以概括为: 图片中的每一个非零像素点都有可能是一个潜在的圆上的一点. 通过投票, 生成累积数量或是累积权重来确定圆. 这种方法能够准确的提取圆心, 如图2所示为霍夫圆变换对小球的识别.

|
图 2 霍夫圆变换对小球的识别 |
1.2 基于LK光流法的改进
通过霍夫圆变换可以确定小球的圆心位置从而得到圆心坐标(x,y), 通过求取该点的灰度梯度值
视频预处理主要分为以下几个步骤. 1.提取视频; 2.高斯滤波; 3.增强边缘.
霍夫圆变换的边缘检测算法利用的是图像强度的一阶和二阶导数, 不过导数对噪声很敏感, 通常情况下图片或多或少都会存在一定的噪点, 因此必须采用滤波器来改善图片的噪声质量, 本文采用的是高斯滤波. 同时增强边缘的目的是为了更加有效的提取轮廓线, 因此需要对图像进行灰度化处理其次修改对比度增强边缘. 之后对视频的预处理结束之后进行小球的追踪.
1.2.2 修改dp分辨率dp是圆心的累加器图像的分辨率与输入图像之比的倒数, 该参数与小球捕捉准确性关系近似为二次函数, 通过调整该参数确定最佳数值提高小球捕捉准确性.
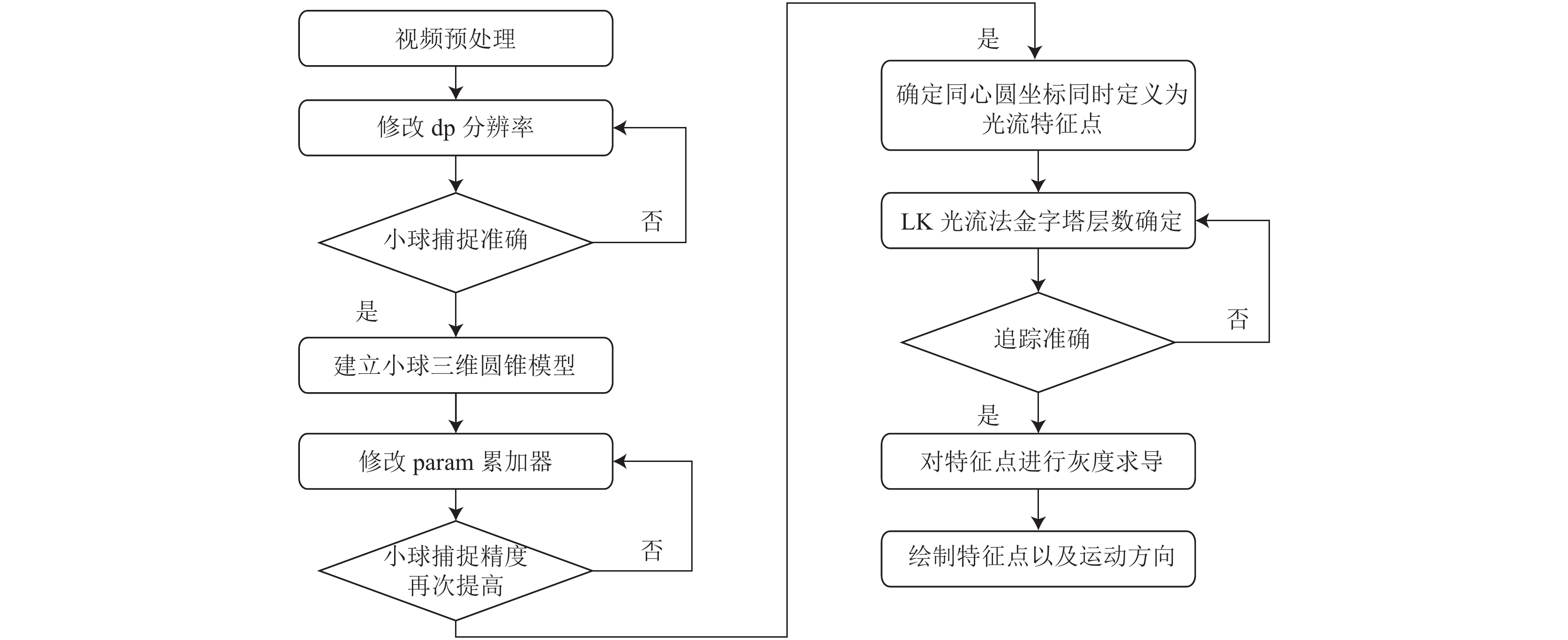
|
图 3 改进LK光流法流程图 |
1.2.3 建立小球三维圆锥模型
在笛卡尔坐标系中圆的方程表示为:
| $ {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2} $ | (1) |
其中, (a, b)是圆心, r是半径, 用极坐标方程表述为:
| $ \left\{ \begin{gathered} {{a}} = {x\rm{ - rcos}}\theta \\ {{b}} = {y\rm{ - rsin}}\theta \end{gathered} \right. $ | (2) |
令笛卡尔坐标系是图像空间, 构造abr三维坐标系作为参数空间, 在参数空间中的一个点对应图像空间的一个圆, 于是笛卡尔坐标系中经过某一点的所有圆映射到abr坐标系中就是一条三维圆锥. 经过笛卡尔坐标系中所有的非零像素点的所有圆就构成了abr坐标系中很多条三维圆锥. 因为笛卡尔坐标系中同一个圆上的所有点的圆方程是一样的, 它们映射到abr坐标系中的的点也就是是同一个点, 在abr坐标系中该点就应该有圆的总像素N0个曲线相交. 只要判断abr中每一点的相交(累积)数量, 大于一定阈值的点就认为是小球, 接下来获得确切的半径范围, 以及圆心坐标(x,y), 将小球模型得到的圆心坐标(x,y)确立为特征点.
1.2.4 修改param累加器param2表示检测阶段圆心累加器的阈值, 同样该参数与小球捕捉准确性关系近似为二次函数, 通过调整该参数确定最佳数值再次提高小球捕捉准确性.
1.2.5 LK光流法金字塔层数确定在LK法中金字塔金字塔主要解决相邻帧之间特征点位移变化较大, 光流法追踪不准确的问题. 通过提高金字塔层数来提高LK法追踪精度.
1.2.6 对特征点进行灰度求导对于该特征点(x,y)在时刻t的灰度为定义为
| $u = \frac{{dx}}{{dt}},v = \frac{{dy}}{{dt}}$ |
经过
| $ \left[ {\begin{array}{*{20}{c}} {Ex} \\ {Ex} \\ {Ex} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {Ex + \Delta y} \\ {Ey + \Delta y} \\ {Et + \Delta t} \end{array}} \right] $ | (3) |
对
| $\begin{aligned} \left[ {\begin{array}{*{20}{c}} {Ex + \Delta x}\\ {Ey + \Delta y}\\ {Et + \Delta t} \end{array}} \right]{\rm{ = }}&\left[ {\begin{array}{*{20}{c}} {Ex}\\ {Ey}\\ {Et} \end{array}} \right]{\rm{ + }}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial Ex}}{{dx}} \cdot \frac{{dx}}{{dt}}}\\ 0\\ 0 \end{array}} \right]{\rm{ + }}\left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{\partial Ey}}{{dy}} \cdot \frac{{dy}}{{dt}}}\\ 0 \end{array}} \right]\\ &{\rm{ + }}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{{\partial Et}}{{dt}} \cdot \frac{{dt}}{{dt}}} \end{array}} \right]{\rm{ + }}\varepsilon \end{aligned}$ | (4) |
带入式(3)化简得
| $ 0=\left[ {\begin{array}{*{20}{c}} {\frac{{\partial Ex}}{{{\rm{d}}x}} \cdot \frac{{{\rm{d}}x}}{{{\rm{d}}t}}} \\ 0 \\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{{\partial Ey}}{{{\rm{d}}y}} \cdot \frac{{{\rm{d}}y}}{{{\rm{d}}t}}} \\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\frac{{\partial Et}}{{{\rm{d}}t}}} \end{array}} \right] $ | (5) |
令
| $ {I_x}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + {I_y}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + {I_t}=0 $ | (6) |
对下一帧图片的像素点坐标(x,y)的邻域范围内进行灰度求导得出一系列新的水平分量和垂直分量, 利用式(6)确定亮度不变点为追踪点, 最后, 绘制特征点以及运动方向.
2 实验本文的实验均为同一台电脑, 基本配置如下: CPU: i5-7300HQ, 内存: 8 GB DDR4 2400 MHZ, 摄像头: 720 P.
为了后续实验的方便进行, 利用灰度直方图对以下三幅背景图片进行定义.

|
图 4 背景图片及其直方图 |
由图4中(a)的灰度直方图分布十分集中, 标准差0.865132和灰度均值0.163566最低, 定义为简单背景. 图4(b)的灰度直方图分布相对图4(c)的灰度直方图分布相对来说较为松散, 标准差32.6324和灰度均值53.3734处于图4(a)、(c)中间, 定义为相对复杂背景. 图4(c)的灰度直方图分布相对图4(b)的灰度直方图分布更为松散, 标准差60.0307和灰度均值61.7127最高, 定义为复杂背景.
本实验主要分为以下两个部分, 第一部分关于改进光流法参数的选定以及准确率的影响, 第二部分在三种不同背景环境下比较反向直方图投影法、LK法以及改进LK对小球追踪速度.
2.1 相关参数的选择 2.1.1 dp参数dp是圆心的累加器图像的分辨率与输入图像之比的倒数, 此参数允许创建比输入图像分辨率低的累加器. dp累加器与输入图像分辨率成反比关系dp=1, 累加器和输入图像分辨率相等, 当dp=2累加器分辨率仅为输入图像的一半高度和宽度. 在板球系统中测试区间为[1,4]的dp值对小球捕捉的影响, 测试结果如图5所示.

|
图 5 dp值与准确率关系 |
当dp值处于2.5时准确率最高, 当dp∈[1,2.5)会出现捕捉不上圆的情况, dp值越小越难捕捉如图6(a), 当dp∈(2.5,4]会捕捉不存在的圆, dp值越大捕捉的不存在圆越多如图6(b).

|
图 6 dp值引起的误差 |
2.1.2 param2参数
param2表示检测阶段圆心累加器的阈值. 阈值越小, 则检测到更多根本不存在的圆, 反之越大, 通过检测的圆更为接近标准的圆. 在板球系统中测试区间为[80,200] 的param2值对小球捕捉的影响, 测试结果如图7所示.

|
图 7 param2值与准确率关系 |
当param2值处于param2∈[140,150]时准确率最高, 当param2∈[80,140)会出现捕捉不存在圆的情况如图8(a), 当param2∈(150,200]会捕捉不上的圆如图8(b).

|
图 8 param2值引起的误差 |
2.1.3 maxLevel参数
在LK法中金字塔层数是影响着图像光流变化准确性的一个重要因素, 金字塔主要解决相邻帧之间变化较大, 光流法追踪不准确的问题.假设底层L0为800×800分辨率的图像, 若两帧之间像素点位移为50×50, 使用金字塔迭代至第Ln层, 图像尺寸和像素点位移均缩小2L, 使用迭代后的图像进行光流计算, 并将计算得到的光流值逐层带入直至底层L0.
本次取金字塔层数[1,6], 观察金字塔层数对于小球捕捉的影响, 如图9所示.

|
图 9 金字塔层数与准确率关系 |
当金字塔层数[1,6]时, 准确率非常的高, 且随着金字塔层数增加也没有明显的变化, 因此选择1层金字塔作为迭代层数.
2.2 不同背景下的小球捕捉的速度分别使用反向直方图投影法、LK光流法以及改进LK光流法在简单背景相对复杂背景以及复杂背景三种情况下对小球进行捕捉跟踪如图10所示(时间为1 min).

|
图 10 上述三种方法在不同的背景下追踪小球 |
上述三种方法分别在简单背景、相对复杂背景及复杂背景下对小球目标追踪进行, 追踪小球的每一循环程序平均运行时间数如表1.
| 表 1 运行时间(ms) |
3 结果与讨论
所有光学镜头都存在几何失真, 几何失真是由于镜头平面不同区域对图像放大率不同而形成的变形现象, 该现象在画面两边最为明显.因而导致了小球成像并非一个完整的圆, 因此不能要求dp值最低和param2值最高.
霍夫圆变换的边缘检测算法利用的是图像强度的一阶和二阶导数, 当图像噪点过大会影响边缘检测的准确值, 应当选取成像噪点小的摄像头.
LK法中增加金字塔迭代层数对于小球捕捉准确率几乎没有影响, 主要因为在板球系统中小球的运动速度不高, 视频尺寸不大, 图像没有出现不连贯的情况, 发挥不出金字塔迭代的优势.
通过表1可以看出反向直方图追踪小球在三种背景下追踪小球十分稳定, 同时小球目标追踪方框流畅没有出现追踪卡顿或者目标丢失情况.但是随着背景复杂程度的提高, 运行速度逐渐减慢. 总体而言反向直方图法表现良好, 但是从程序运行速度上看, 该方法运行速度还是不够理想.
可以发现无论是应对简单背景还是复杂背景, 光流法捕捉目标十分稳定, 从运行速度来看LK法在这三种情况下分别提高了27.77、42.76、57.53倍, 运行速度有一个很大的提高.同时面对三种不同情况的背景该方法的运行速度相差很小.
修改后的光流法与反向直方图法相比, 运行速度分别提高了33.48、42.76、69.49倍. 虽然基于LK的改进方法运行速度较传统的LK法没有明显的提高, 但是改良了传统LK法无法直接捕捉小球圆心这一弊端, 可以直接定位圆心位置坐标方便后续板球系统的控制.提高了后续控制的精度. 究其原因是因为该反向直方图投影法匹配时采用的是平方差匹配法, 其原理公式如下:
| $R(x,y) = \sum\limits_{x',y'} {(T(x',y') - I(x + x',y + y'))} $ | (7) |
若匹配的平方差为0则为最优, 反之数值越大则越差.假设(x,y)为模板像素矩阵, (x’,y’)为图像归一化后的像素矩阵, 由公式(7)可以得到为了得到与模板相匹配的目标需要用模板对归一化后的每一个像素矩阵进行匹配, 计算平方差.相当于对图像的每一个像素都进行了运算, 运算量庞大, 所以导致了反向直方图法与两种光流算法相比运行速度最慢.
LK光流法主要是通过角点进行追踪, 角点主要提取的是灰度梯度较大的地方, 而这些地方通常存在于物体的边界. 同时角点的数量可通过精度的设置来改变, 只需要对角点及其邻域的像素进行计算, 与反向直方图相比像素点计算数量大幅度减少, 所以速度提升非常快.
改进LK光流法只需计算一个像素点及其邻域像素, 与传统LK法相比像素点的计算数量又一次降低, 但是由于减少的像素点数量跨度很小, 速度与LK法相比提升不是十分明显.
4 结束语本文采用反向直方图投影法、LK法以及改进后的LK法在三种不同的背景下对小球进行追踪, 改进后的LK光流法更为适合板球系统中对小球的追踪:
(1) 使用LK法追踪小球相较反向直方图投影法大幅度提高了运行速度, 但无法捕捉球心坐标.
(2) 通过将霍夫圆变换引入LK法得到改进的光流法, 对小球进行追踪, 小球球心点不会丢失, 追踪准确.
| [1] |
韩洁. 基于果蝇优化算法的视觉板球系统控制研究[硕士学位论文]. 重庆: 西南大学, 2017.
|
| [2] |
李晓飞. 高速在线机器视觉检测方法的研究[硕士学位论文]. 天津: 天津理工大学, 2008.
|
| [3] |
Grabe V, Bülthoff HH, Giordano PR. A comparison of scale estimation schemes for a quadrotor UAV based on optical flow and IMU measurements. IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan. 2013. 5193–5200.
|
| [4] |
张辰, 赵红颖, 钱旭. 直方图反向投影多目标检测优化算法. 计算机系统应用, 2014, 23(2): 178-182. DOI:10.3969/j.issn.1003-3254.2014.02.032 |
| [5] |
王思远, 姚志均. 一种快速稳定的对比度跟踪方法. 舰船电子对抗, 2017, 40(5): 81-83, 108. |
| [6] |
许文韬. 纹理图像特征提取与分类研究[博士学位论文]. 上海: 华东师范大学, 2017.
|
| [7] |
Horn BKP, Schunck BG. Determining optical flow. Artificial Intelligence, 1981, 17(1–3): 185-203. DOI:10.1016/0004-3702(81)90024-2 |
| [8] |
Barron J L, Fleet D J, Beauchemin S S, et al. Performance of optical flow techniques. Proceedings 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Champaign, IL, USA. 1992. 236–242.
|
| [9] |
屈治华, 邵毅明, 邓天民. 基于特征光流的多运动目标检测跟踪算法与评价. 科学技术与工程, 2018, 18(22): 97-104. DOI:10.3969/j.issn.1671-1815.2018.22.014 |
| [10] |
Lucas BD, Kanade T. An iterative image registration technique with an application to stereo vision. Proceedings of the 7th International Joint Conference on Artificial Intelligence. San Francisco, CA, USA. 1981. 674–679.
|
| [11] |
毛庆洲, 潘志敏, 高文武. 利用迭代霍夫圆变换实现成捆棒材可靠计数. 武汉大学学报·信息科学版, 2014, 39(3): 373-378. |
| [12] |
Sharmin N, Brad R. Optimal filter estimation for Lucas-Kanade optical flow. Sensors, 2012, 12(9): 12694-12709. DOI:10.3390/s120912694 |
 2019, Vol. 28
2019, Vol. 28

