现代社会已经迈入了大数据时代, 海量数据带来的巨大研究价值无论对于国家的宏观调控, 企业的决策分析还是疾病的预防控制等方面的影响都不容忽视. 因此, 政府、企业或者社会机构每年都会收集或者发布大量的数据以供分析研究之用, 而这些数据中通常含有个人不想被公开的敏感信息, 包括个人的疾病、收入等等. 因此, 如何在数据发布时防止个人敏感信息的泄露就成为了一个重要的研究议题. 为此k-匿名模型[1–4]、l-多样性模型[5–7]和t-接近模型[8,9]等匿名模型相继被提出, 这些模型大多采用将准标识符属性泛化和增加敏感属性多样性的方式, 使得攻击者无法确切地推断出一个分组内的某条记录具体属于哪个人, 从而达到防止个人敏感信息泄露的目的. 这些模型针对分类型敏感信息可以起到良好的保护作用, 但是对于数值型敏感属性却不能起到抗近邻泄露的作用. 近邻泄露的概念在文献[10]中被首次提出, 主要是指由于同一个分组内不同记录的数值型敏感属性值之间距离太过接近, 使得攻击者可以以较大概率推测出其中某条记录的敏感属性值的所在区间而导致敏感信息泄露的情况. 由于数值型敏感属性的特点, 原始数据即便经过以上几种匿名模型的处理, 敏感信息仍然会有发生近邻泄漏的风险, 因为只是增加一个分组内敏感属性值的多样性而不对敏感属性值间的距离加以限制, 如果一个分组内的敏感属性值集中分布在一个较小区间内, 那么攻击者通过背景信息确定被攻击者所在的分组后, 就可以在不需要知道被攻击者的确切敏感属性值的情况下获取到被攻击者敏感属性值的大致范围, 从而导致近邻泄漏发生. 针对数值型敏感属性易发生近邻泄漏这一问题, 本文提出了一种新的匿名模型——(εi, k)-匿名模型, 该模型首先基于聚类方法将按照升序排列的敏感属性值划分到多个值域区间内, 然后通过对每个值域区间设置相应的阈值εi来控制该子区间内敏感属性值的接近程度, 最后通过将准标识属性和敏感属性分开发布的方式来提高数据的可用性.
2 相关工作针对抗数值型敏感属性近邻泄漏问题, 文献[11]提出了(k, e)-匿名模型, 该模型要求每个分组内至少要包含k条记录, 并且要求每个分组内最大和最小敏感属性值的差值要大于等于阈值e, 以此来达到扩大分组内敏感属性值分布范围的目的. 但是由于没有对分组内的敏感属性值的分布情况加以限制, 在阈值e设置的足够大的条件下, 如果分组内的大部分敏感属性值集中分布在一个密集区域内, 那么攻击者仍然可以以较大的概率推断出某个人的敏感属性值所在的大致区间, 从而导致近邻泄露的发生. 文献[10]提出了(ε, m)-匿名模型, 该模型要求对于每个分组内的每条记录t, 若其敏感属性值是x, 那么在这个分组中, 敏感属性值落在区间[x–ε, x+ε]内的记录数不能超过该分组内元组总数的1/m, 其中ε是为了控制每个分组内敏感属性值之间的接近程度而设置的阈值. 该模型对整个敏感属性值值域区间只设置一个阈值ε, 这种单一的阈值ε可能无法满足实际使用需求, 尤其是当敏感属性值集中分布在几个相距较远的区间时. 因为不同敏感属性值的敏感度不同, 相距较远的不同区间内的敏感属性间敏感度的差异则更大, 单一的阈值ε无法满足敏感属性值敏感度多样性所带来的阈值多样性的要求. 文献[12]提出了分级l-多样性模型, 该模型首先需要将数值型敏感属性值域分级, 再基于分级信息实现数值型敏感属性的l-多样性. 由于该模型增加了分组内分级域多样性的要求, 可以看作是加强的l-多样性模型, 主要目的是提高同一个分组内敏感属性值的相异度以达到抵抗近邻泄露的目的. 该文献要求等距离对敏感属性值域进行区间划分, 然后再对每个区间设置等级, 按照等距离原则划分区间没有考虑区间内敏感属性值的分布情况, 这样还是可能导致出现一个分组内敏感属性值过于接近的问题, 从而引发近邻泄露.
为了更加有效地解决数值型敏感属性近邻泄露问题, 在之前文献工作的基础上, 本文面向数值型敏感属性提出了一种新的匿名模型——(εi, k)-匿名模型. 首先该模型通过按照敏感属性的灵敏度划分敏感属性值域区间, 克服了以往区间划分方案的不足之处; 其次, 通过对每个值域区间设置不同的阈值εi克服了以往设置单一阈值没有考虑不同敏感属性值敏感度不同的缺点. 最后通过理论分析和仿真实验验证了本文所提出的(εi, k)-匿名模型在信息可用性和执行效率方面的优越性.
3 面向数值型敏感属性(εi, k)-匿名模型本文提出的(εi, k)-匿名模型主要包括以下内容: 敏感属性值域区间划分算法、(εi, k)-匿名原则和最大桶优先提取算法. 首先根据基于敏感属性值间的距离将敏感属性值划分到若干值域区间内, 然后为每个区间设置一个阈值εi, 通过最大桶优先提取算法使生成的匿名表中的每个分组满足(εi, k)-匿名原则, 以此来降低每个分组内敏感属性值的近邻泄露风险. 接下来将对提出的(εi, k)-匿名模型展开详细的介绍.
3.1 敏感属性值域区间划分算法解决数值型敏感属性近邻泄漏问题, 首要的工作是对敏感属性值值域区间进行划分. 文献[12]采用等间距法划分区间, 将敏感属性值值域划分成若干个长度相同的区间, 该方法简单易行但缺点明显, 就是没有考虑敏感属性值的分布情况和不同敏感属性值敏感度的不同, 从而可能导致大量的信息损失. 文献[13]中的极大熵法采取了一个使熵最大化、信息损失量最小化的原则来划分区间. 一般来说区间的个数越多, 信息损失量就越小. 然而, 该方法受到样本容量、最多区间个数等方面的制约, 很难做到使熵最大化[14].
为了弥补以上办法的不足, 本文按照“高内聚低耦合”的原则基于敏感属性值间的距离对区间进行划分, 使得同一区间内的属性值尽量集中分布, 不同区间的属性值则尽量远离. 在正式提出本文的区间划分算法之前, 先给出以下定义.
定义1(敏感属性值的敏感度). 敏感属性值间的距离对敏感属性值近邻泄露风险程度的影响随着敏感属性值的增大而增大, 敏感属性的这种性质被称为“敏感度”.
定义2(相对欧氏距离). 对于单维数值型敏感属性值v1、v2(为了方便说明假设v2≥v1≥0)而言, 其欧氏距离[14]d12=v2–v1, 则v1和v2之间的相对欧氏距离表示为
下面给出如下定理.
定理1. 任意两个敏感属性值间的相对欧氏距离在区间[0, 1)内.
证明.
推论1. 两点之间的相对欧氏距离与欧氏距离之间不具有正相关性.
证明. 采用反证法, 设坐标轴上有以下四个点P1、P2、P3、P4, 其坐标值依次为10、20、1000、1020, 则P1和P2之间的欧氏距离d12等于10, 相对欧氏距离
推论2. 如果两点间的欧氏距离相同, 那么敏感属性值取值越大, 则相应的相对欧氏距离越小.
证明. 假设两点间的欧氏距离d12=v2–v1, 则v2=v1+d12, 则
有了相对欧氏距离作为距离度量标准之后, 下面正式提出本文的敏感属性值域区间划分算法(假定数轴上一共存在有b个点).
1)将各条记录的敏感属性值提取出来按照升序方式以此排列在数轴上.
2)计算数轴上每两个相邻点之间的相对欧氏距离
3)求出平均相对欧氏距离:
4)比较每两个敏感属性值间的相对欧氏距离
5)当步骤4)全部完成后, 生成所有的敏感属性值域区间.
值得注意的是, 在第4)步中, 本文以平均相对欧氏距离作为比较的基准, 用户也可以根据实际需要, 将平均相对欧氏距离乘以参数w (w的取值在0.5到1之间为宜)来作为比较时的参照距离. 下面通过一个示例来对算法的执行过程进行说明. 若原始数据表包含如下敏感属性值100、150、4500、5200、4800、200, 首先将这些敏感属性值按升序排列成100、150、200、4500、4800、5200的形式, 计算出相邻两点间的相对欧氏距离分别为0.2、0.143、0.915、0.032、0.04, 取平均相对欧氏距离(
在正式提出本文的(εi, k)-匿名原则之前, 首先给出以下定义. 给定数据表T, SA是T的敏感属性, 其中记录t的敏感属性值为V, 用t.SA来表示记录t的敏感属性值大小.
定义3(区间阈值εi). 在划分完敏感属性值域区间后, 需要为每个敏感属性值域区间Pi(i=1, …, n)设置一个阈值εi(i=1, …, n)来控制该值域区间内数值之间的接近程度.
定义4(t的εi邻域I(t)). 对于区间Pi(i=1, …, n)中的记录t来说, 其εi邻域表示为I(t)= [t.SA–εi, t.SA+εi].
定义5(t的εi邻域集N(t)). 给定数据表T’, t是分组E中的任意元组, 记录t的εi邻域集N(t)表示在敏感属性值域区间内落在记录t的εi邻域I(t)内的记录的集合, N(t)={t’|t’≠t, t’.SA=Vj, Vj
定义6(t的近邻泄露风险). 对于给定的数据表T’, 分组E中的任意一条记录t的近邻泄露风险定义为: Pbrh(t, εi)=|N(t)|/|E|, 其中|E|表示分组E中所包含元组的数目.
给出以上定义之后, 下面正式提出(εi, k)-匿名原则. 给定数据表T’, 如果对于T’中的所有的分组E都满足以下条件, 则称T’是满足(εi, k)-匿名原则的:
1) 每个分组内包含的元组数|E|在区间[k, 2k]之间.
2)每个分组内至少包含k条εi邻域没有交集的记录.
定理2. 若给定数据表T’满足(εi, k)-匿名原则, 那么对于表中任意元组E中的每条记录t来说, 其敏感属性值近邻泄露风险≤1/2.
证明. 由于满足(εi, k)-匿名原则的每个分组内元组数目|E|限定在[k, 2k]区间内, 且每个分组内至少包含k条εi邻域没有交集的记录, 那么单就看这k条记录是不存在近邻泄露风险的, 考虑在最坏情况下, 剩余的|E|–k条记录全部落在记录t的εi邻域内, 那么在该分组内, 记录t的近邻泄露风险最大, Pbrh(t, εi)=(|E|– k)/|E|=1–k/|E|, 当|E|=2k时, Pbrh(t, εi)取得最大值1/2, 证毕.
3.3 最大桶优先提取算法为了生成满足(εi, k)-匿名原则的匿名数据表T’, 本文提出了一种最大桶优先提取算法, 该算法首先桶按照桶内元组的数目降序排列, 然后从前k个桶中提取出k条εi邻域没有交集的记录, 依次迭代进行, 最后将未分配分组的元组按(εi, k)-匿名原则的要求分配到合适的桶中, 从而生成满足(εi, k)-匿名原则的匿名数据表T’. 在介绍算法之前, 先引出相关概念.
定义7(桶). 将敏感属性值域区间Pi(i=1, …, n)以其设定阈值εi(i=1, …, n)为间隔划分形成的小区间Sij(i=1, …, n, l mod εi≥ j–1≥0, l是区间长度)称为桶.
定义8(相邻桶). 来自同一个值域区间Pi(i= 1, …, n)的两个桶Sij(i=1, …, n, l mod εi≥ j–1≥0)如果是相邻的, 则称这两个桶是相邻桶.
定义9(桶的容量). 桶的容量 每个桶内所包含元组的数目称之为桶的容量.
给出了以上定义之后, 下面给出最大桶优先提取算法, 具体算法如下.
输入: 原始数据表T, 每个分组内至少包含的元组数k.
输出: 只包含准标识符属性的数据表QIT, 只包含敏感属性的数据表ST.
1) 首先对原始表T中的记录根据其敏感属性值的大小进行升序排列.
2)第一次划分区间: 见3.1节敏感属性值域区间划分算法.
3)为每个值域区间设置相应的阈值εi(由于数值敏感度的影响, 值域区间内的数值越大, 相应的该区间的阈值设置越高).
4)第二次划分区间: 对每个值域区间以对应的阈值为间隔再次划分, 生成若干个桶.
5)根据桶内元组的数目, 对得到的桶按降序处理.
6)将前k个桶的第一条记录都提取出来.
7)判断: 如果这k个桶全部是非相邻的, 那么则可以直接将这k条记录放到第一个分组内. 如果这k个桶中含有相邻桶, 则需要进行判断, 如果这两个敏感属性值来自同一个值域区间, 那么比较其差值是否大于该区间设定的阈值, 如果大于则满足提取条件可以直接提取, 如果差值小于阈值, 那么值域较小桶内提取记录不变, 从值域较大桶内的第二条记录开始逐次提取, 直到满足两条记录的差值大于该区间设定的阈值. 如果无法找到这样的两条记录, 那么说明这两个桶内的数据分布过于接近, 则隐藏其中的一个桶, 提取第k+1个桶重新比较, 直到找到满足条件的k条记录为止.
8)提取结束之后, 将提取出来的记录从桶内剔除, 按桶内元组的数量将桶重新降序排序.
9)如果含有元组的桶的数量大于k个, 则重复执行6)至8)步骤, 每经过一个循环就会形成一个新的分组, 直到含有记录的桶的数目小于k个为止或者剩余k个但是提取不出满足条件的记录为止.
10)对于剩余桶内的记录, 将其插入到已经存在的分组内, 使得每个分组都满足(εi, k)- 匿名原则.
11)输出一个准标识符表格QIT和敏感属性表ST, 这样就得到了满足(εi, k)- 匿名原则的数据表格.
4 实验结果及分析本章节通过实验分析验证(εi, k)- 匿名模型的性能, 并将其同文献[10]中的(ε, m)-anonymity模型和文献[12]中的分级l-多样性模型进行比较. 实验所采用的数据集是真实数据集SAL, 数据集来自http://ipums.org/. 该数据集被广泛应用作为实验测试数据集. 该数据集共包含了50万个元组, 每个元组记录了一个美国人的个人信息, 本文提取了其中七个属性进行研究, 其中{Age, Sex, Race, Country, Birthplace, Occupation}作为准标识符属性, Income作为敏感属性进行研究. 本文将从信息可用性、算法执行效率和两个方面对三种方案进行比较.
4.1 信息可用性分析在分析数据的可用性时, 可以通过文献[15]中的构造集合查询语句的方式进行分析. 查询语句的形式如下所示:
select count(*) from SAL
where A1∈ b1 and A2 ∈ b2 and …Aw–1 ∈bw–1 and Aw∈bw
其中, 参数w被称作查询维度. A1, A2, …, Aw–1是w–1个准标识符属性, Aw是敏感属性, bi(1≤i≤w)是属性Ai的值域中的一个随机区间.
信息可用性的高低采用平均相对误差进行衡量. 平均相对误差用公式表示为ARErr = (act–est)/act. 其中, act表示查询原始数据表得到的精确结果, est表示查询匿名后的数据表得到的结果. 平均相对误差越低说明信息可用性越高; 否则, 信息可用性越差.
图1~图3分别描述了数据集大小、准标识符属性维数和ε(εi)值的变化对(εi, k)-匿名模型、(ε, m)-anonymity和分级l-多样性模型的影响.
|
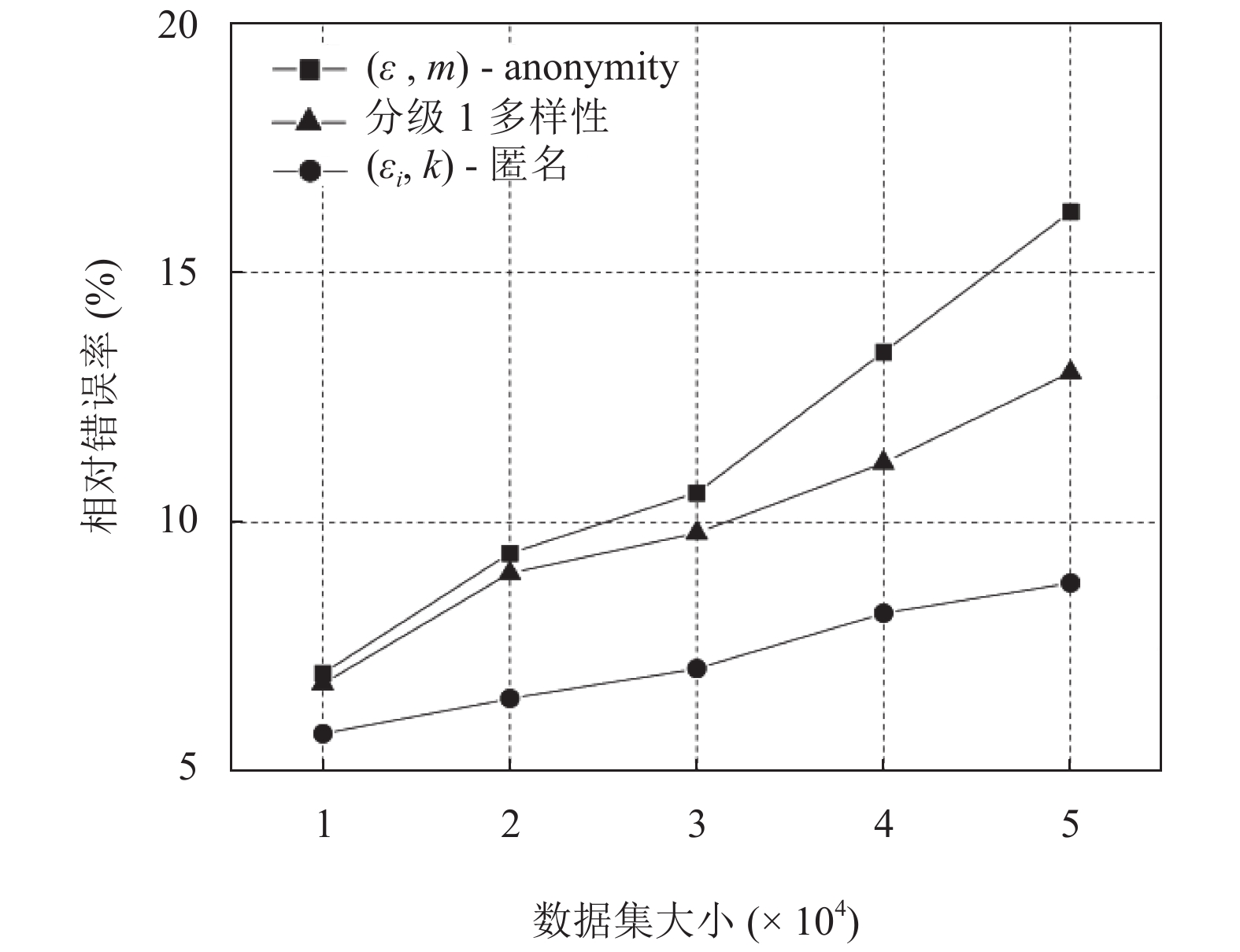
图 1 数据集大小对信息可用性的影响 |
由图1可知, 随着数据集大小逐渐增大, (ε, m)-anonymity和分级l-多样性模型的相对错误率逐渐增大, 这是由于随着数据集的增加, 准标识符属性的泛化区间增加, 这样就会造成更多的信息损失, 导致数据可用性下降. 而(εi, k)-匿名模型的相对错误率则随着数据集的增大而波动较小且其相对错误率一直低于(ε, m)-anonymity和分级l-多样性, 这是因为(εi, k)-匿名模型并未采用对准标识符属性泛化的方式来保护隐私, 而是采用有损链接的方式将准确的准标识符属性和敏感属性分开发布, 这样就减少了泛化所带来的信息损失, 同时也减少了数据集大小变化所带来的影响.

|
图 2 准标识符属性个数对信息可用性的影响 |
由图2可知, 随着准标识符属性的增加, (ε, m)-anonymity和分级l-多样性模型的相对错误率逐渐增大, 这是因为准标识符属性维数的增大使在每个元组上进行泛化的属性数目增加, 在泛化过程中的信息损失也将增大, 但是(εi, k)-匿名模型的相对错误率则受准标识符属性维数变化的影响较小且低于(ε, m)-anonymity和分级l-多样性, 理由同上.

|
图 3 ε(εi)值的变化对信息可用性的影响 |
在图3中, 由于l-多样性模型没有参数ε(εi), 因此只比较了ε(εi)的变化对(ε, m)-anonymity和(εi, k)-匿名模型的影响, 为了方便比较, 对于(ε, m)-anonymity, 选择参数β, 令ε=βr, r表示整个敏感属性值区间的长度, 对于(εi, k)-匿名模型, 令εi=βri(1≤i≤n) , ri表示每个敏感属性值域区间的长度, 由图3可知, 随着参数β的增大(ε和εi也随之增大), (ε, m)-anonymity和(εi, k)-匿名模型的相对错误率都会随之增大, 这是因为阈值ε(εi)越大, 对敏感属性的保护程度越高, 不可避免的会导致信息的可用性下降.
综合上面对图1~图3的分析可以看出, 本文所提出的(εi, k)-匿名模型同文献[10]中的(ε, m)-anonymity和文献[12]所提出的l-多样性模型相比, 在数据集大小、准标识符属性个数和ε(εi)值变化三者的影响下, (εi, k)-匿名模型的信息的可用性都是最高的.
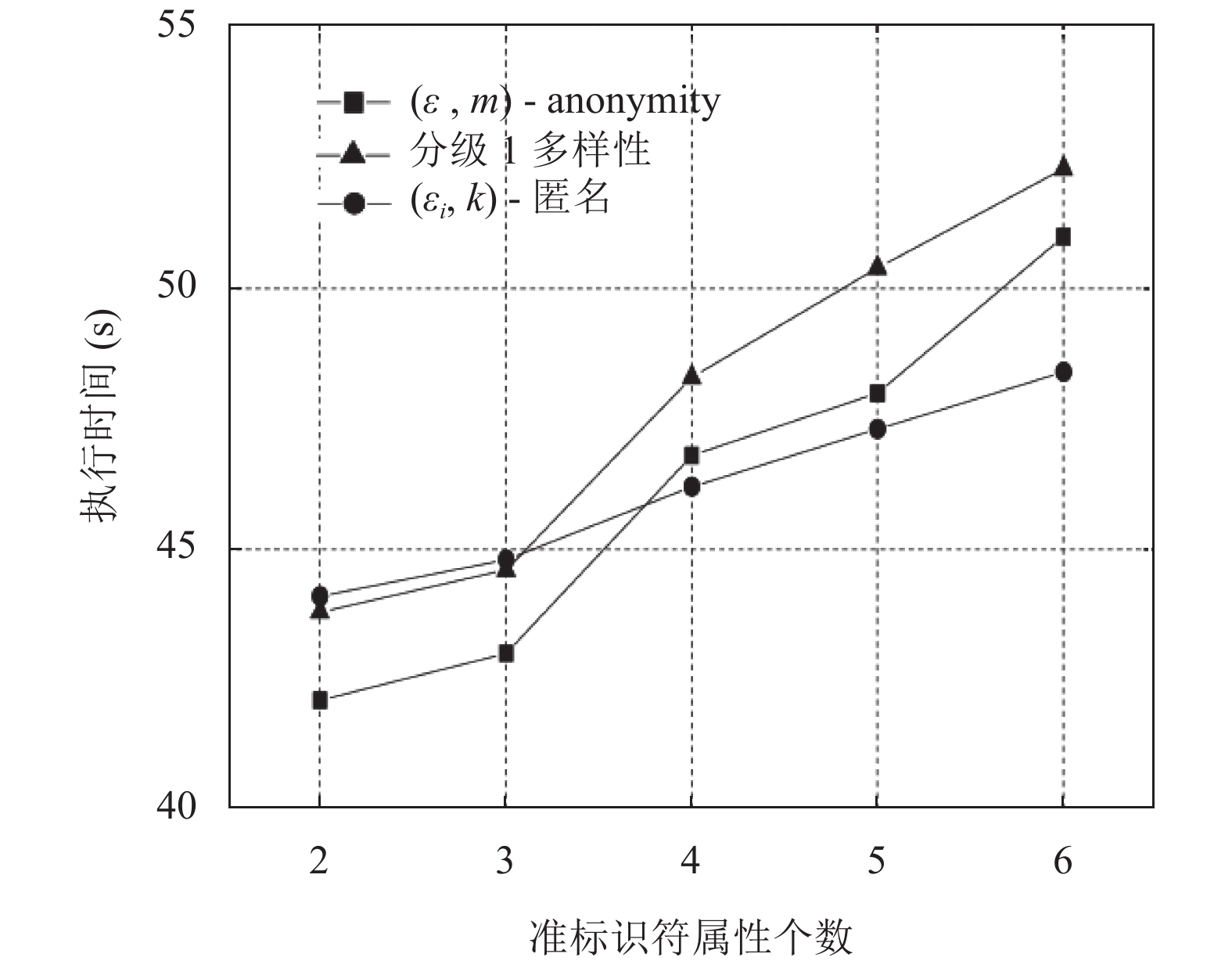
4.2 算法执行效率分析图4表示准标识符属性维数对算法执行时间的影响, 由图4可知, 随着准标识符属性维数的增加, 分级l-多样性和(ε, m)-anonymity执行时间增加明显, (εi, k)-匿名模型则基本保持不变. 这是由于(εi, k)-匿名模型不需要对准标识符属性进行泛化, 所以基本不受准标识符属性维数增加的影响, 而随着准标识符属性的增加, 分级l-多样性和(ε, m)-anonymity需要泛化的属性增多, 导致执行时间上升. 值得注意的是, 当敏感属性值维数较少时, (εi, k)-匿名模型的执行时间大于分级l-多样性和(ε, m)-anonymity, 这是由于(εi, k)-匿名模型增加了对敏感属性值划分区间的算法, 导致其执行时间增加.
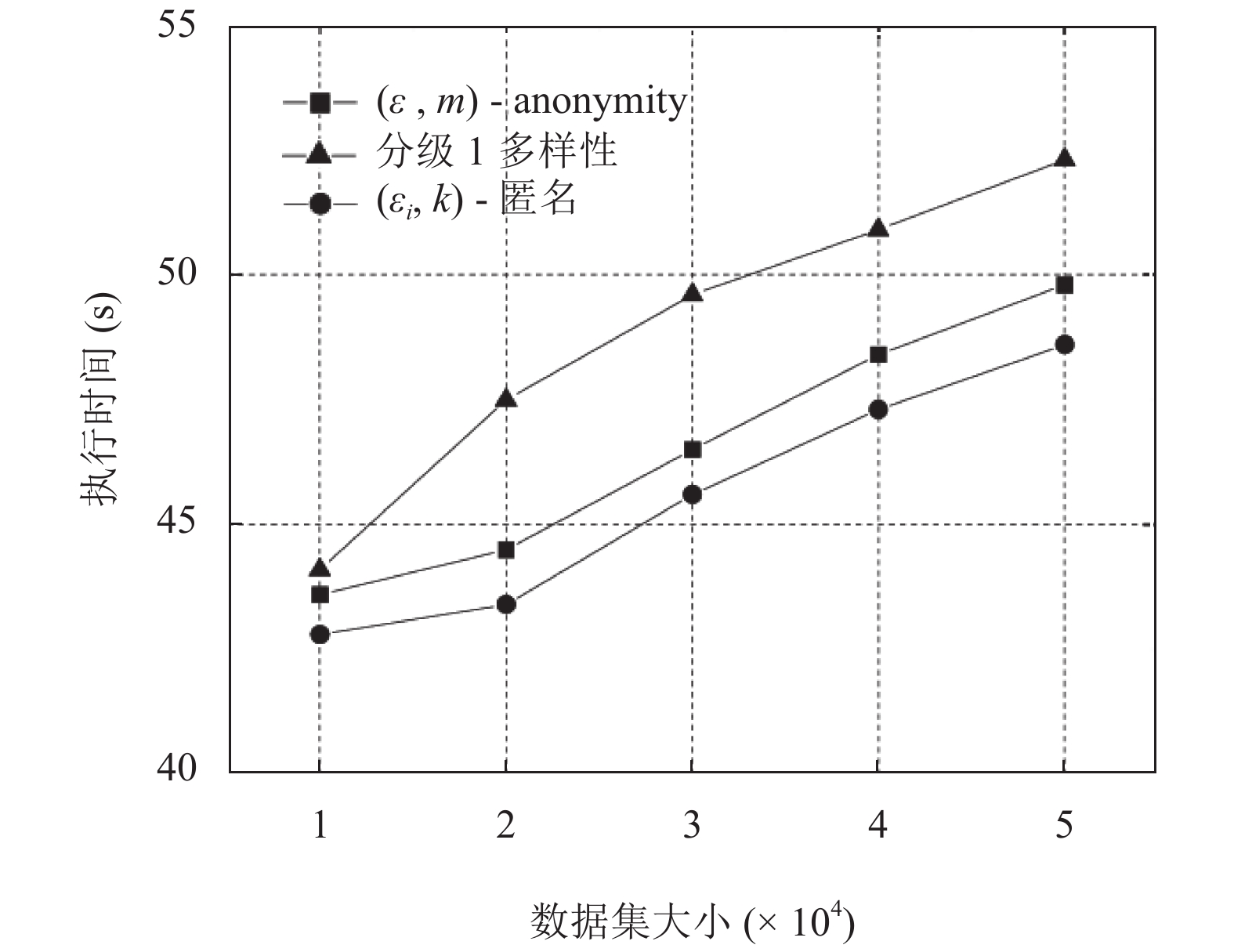
图5表示数据集大小对三种方案执行时间的影响, 由图可知, 随着数据集的增大, 三种方案需要处理的元组增加, 执行时间都呈上升趋势.
|
图 4 准标识符属性个数对算法执行时间的影响 |
|
图 5 数据集大小对算法执行时间的影响 |
综合上面对图4~图5的分析可以看出, 在算法执行效率方面, (εi, k)-匿名模型同(ε, m)-anonymity和分级l-多样性模型相比, 在准标识符属性较少时, (εi, k)-匿名模型的执行效率略低于(ε, m)-anonymity和分级l-多样性模型, 但是随着准标识符属性个数的增加, (εi, k)-匿名模型执行效率开始反超(ε, m)-anonymity和分级l-多样性模型; 随着数据集的逐渐增大, (εi, k)-匿名模型的执行效率总是略低于l-多样性模型, 但总是高于(ε, m)-anonymity.
5 结论本文针对数值型敏感属性近邻泄露问题, 提出了一种新的匿名模型——(εi, k)-匿名模型, 该模型通过划分敏感属性值域区间, 为每个敏感值域区间设定相应的阈值εi来控制每个值域区间内敏感值的近邻泄露风险. 理论分析和试验结果表明, 该模型能够在有效抵御数值型敏感属性近邻泄露攻击的同时保证了较高的数据可用性和较高的执行效率, 可以作为现有隐私保护技术手段的有效补充.
| [1] |
Sweeney L. k-anonymity: A model for protecting privacy
. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570. DOI:10.1142/S0218488502001648 |
| [2] |
Pramanik I, Lau RYK, Zhang WP. K-anonymity through the enhanced clustering method. Proceedings of the 2016 IEEE 13th International Conference on e-Business Engineering. Macau, China, 2016, 85-91. |
| [3] |
Gao YXN, Luo T, Li JF, et al. Research on K anonymity algorithm based on association analysis of data utility. Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference. Chongqing, China, 2017, 426-432. |
| [4] |
吕品, 钟珞, 于文兵, 等. MA-Datafly: 一种支持多属性泛化的k-匿名方法
. 计算机工程与应用, 2013, 49(4): 138-140. DOI:10.3778/j.issn.1002-8331.1107-0183 |
| [5] |
Machanavajjhala A, Kifer D, Gehrke J, et al. L-diversity: Privacy beyond k-anonymity
. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1): 3. DOI:10.1145/1217299 |
| [6] |
Xiao XK, Yi K, Tao YF. The hardness and approximation algorithms for l-diversity. Proceedings of the 13th International Conference on Extending Database Technology. Lausanne, Switzerland, 2010, 135-146. |
| [7] |
Yang GM, Li JZ, Zhang SX, et al. An enhanced l-diversity privacy preservation. Proceedings of the 2013 10th International Conference on Fuzzy Systems and Knowledge Discovery. Shenyang, China, 2013, 1115-1120. |
| [8] |
Li NH, Li TC, Venkatasubramanian S. t-closeness: Privacy beyond k-anonymity and ℓ-diversity. Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering
. Istanbul, Turkey, 2007, 106-115. |
| [9] |
El Ouazzani Z, El Bakkali H. A new technique ensuring privacy in big data: Variable t-closeness for sensitive numerical attributes. Proceedings of the 2017 3rd International Conference of Cloud Computing Technologies and Applications. Rabat, Morocco, 2017, 1-6. |
| [10] |
Li JX, Tao YF, Xiao XK. Preservation of proximity privacy in publishing numerical sensitive data. Proceedings of 2008 ACM SIGMOD International Conference on Management of Data. Vancouver, Canada, 2008, 473-486. |
| [11] |
Zhang Q, Koudas N, Srivastava D, et al. Aggregate query answering on anonymized tables. Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering. Istanbul, Turkey, 2007, 116-125. |
| [12] |
韩建民, 于娟, 虞慧群, 等. 面向数值型敏感属性的分级l-多样性模型
. 计算机研究与发展, 2011, 48(1): 147-158. |
| [13] |
Han JW, Kamber M, Pei J. 数据挖掘: 概念与技术. 范明, 孟小峰, 译. 北京: 机械工业出版社, 2012. 88–90.
|
| [14] |
周志华. 机器学习. 北京: 清华大学出版社, 2016. 39.
|
| [15] |
Xiao XK, Tao YF. Anatomy: Simple and effective privacy preservation. Proceedings of the 32nd International Conference on Very Large Data Bases. Seoul, Korea, 2006. |
 2019, Vol. 28
2019, Vol. 28


