2. 中国石化青岛安全工程研究院, 青岛 266071
2. SINOPEC Qingdao Research Institute of Safety Engineering, Qingdao 266071, China
石油、化工等危险化学品企业属于高危企业, 具有“高温高压、易燃易爆、有毒有害、连续作业、链长面广”等特点. 目前危险化学品安全形势严峻, 各类爆炸、火灾等事故时有发生[1]. 据统计, 我国化工企业9.6万余家, 其中危险化学品生产企业2.4万余家, 生产化学品种类10万余种, 近十年化学品事故超过5000起[2,3]. 危化品事故涉及的点多面广, 一旦事故发生, 严重威胁人民的生命安全, 并造成巨大的社会经济损失[4]. 因此, 针对危化品事故进行分析研究, 并在此基础上制定相应的安全对策, 显得尤为重要.
传统的事故致因模型[5]是建立在“事故是由部件失效引起的”这一假设基础上的, 因此, 事故预防的重点集中在使系统部件具备高可靠性, 或者预知和获取部件的失效时间来预防事故的发生[6]. 基于事件链的事故致因模型直接有效, 是以“因果关系”为导向的, 以分析事故原因作为预测事故的主要依据. 但是它们过于简单没有包含导致事故发生以及如何预防事故所必需的因素. 其主要局限性包括要求直接因果关系, 选择事件的主观性, 识别事件链条件的主观性等. 事故原因分析是一个复杂的系统工程, 涉及各个领域和各个行业的专业知识[7]. 受分析者专业领域知识的限制, 传统的事件链模型无法完全识别控制目标和复杂系统要素间的因果关系, 达不到预期的控制和优化目标.
其次, 事故预测是基于可知的信息和数据, 对预测对象的安全状况进行预报和预测[8]. 传统的事故预测方法的研究重点往往集中在事故预测模型的建立和算法改进上, 而忽略了事故先验数据收集和梳理. 受限于先验数据收集难度和预测模型复杂度的影响, 事故预测模型通常是建立在历年事故发生起数、死亡人数、危化品种类和数量等有限的几个人为认为和危化品事故发生有强因果关系的因素之上的, 这就造成了事故预测结果的不全面和不准确. 以中国石化11.22东黄输油管道泄漏爆炸事故为例, 如果以传统的事件链事故致因模型进行分析, 从因果关系的角度, 是不太可能考虑到市政管网跟爆炸事故之间的强相关关系的[9].
综上所述, 传统的基于因果关系的事故链分析方法受限于传统安全工程所依赖的技术基础和假定, 无法适应于今天所建造的复杂系统. 本文以事故致因理论为基础, 分析危化品事故形成的主要影响因素, 构建了危化品事故状态向量, 全面描述导致危化品事故发生的因素, 并基于构建的状态向量进行危化品事故分析预测应用.
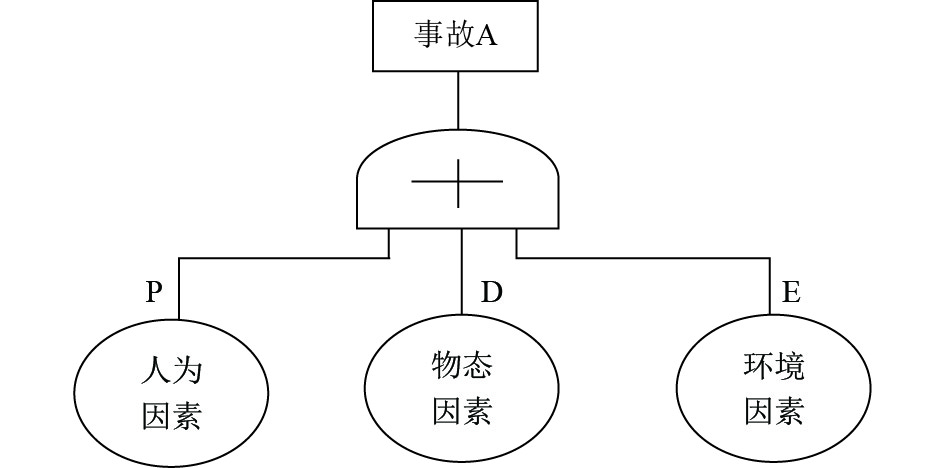
1 危化品事故状态向量 1.1 事故状态向量定义结合事故致因理论, 危化品事故的发生主要由人的不安全因素、物的不安全状态和环境的不安全影响造成的, 因此可将事故复杂性致因模型可归纳为三大类指标: 主观评审指标(人为因素)、客观固有指标(物态因素)、环境指标(环境因素), 如图1所示.
|
图 1 事故复杂性致因模型 |
为了更好的研究事故发生的原因, 开展事故的预测预防, 根据事故复杂性致因模型, 将事故发生前后的状态定义为一个多维向量, 组成向量的各元素由事故复杂性致因模型的各因素组成, 具体如下:
(1) 主观评审指标
主观评审指标由企业定期进行评审打分, 假设主观指标数量为m个, 则主观评审指标可表示为一个m维向量P.
| $ P = \left\{ {P1,P2,\;P3, \cdots, Pm} \right\} $ |
主观评审指标主要是涉及一些无法量化或者无法自动提取的安全指标的获取, 如“对特种设备操作和维护的培训是否到位”, “安全监管行为是否得当”等, 这些指标需要靠企业人员定期评估打分获得.
(2) 客观固有指标
客观固有指标指企业固有危险等级, 假设客观指标数量为n个, 则客观固有指标也可表示为一个n维向量D.
| $ D = \left\{ {D1, D2, D3, \cdots, Dn} \right\} $ |
客观固有指标可自动获取, 如企业“化学品产量”, “重大危险源数量”, “危险物质的火灾、爆炸性指数”, “化学品物质毒性指数”等.
(3) 环境指标
环境指标主要包括企业当地的气候气象、地理地质环境、自然灾害发生频率、政府监管水平、社会事件等相关指标, 一切不能归为前两类的指标都归为环境指标. 这些指标也应该最终对应成t维向量E.
| $ E = \left\{ {E1, E2, E3, \cdots, Et} \right\} $ |
综上, 事故状态向量可定义如下:
事故状态向量A={P, D, E}.
1.2 基于知识图谱的事故状态向量构建方法事故状态向量将事故进行向量化表示, 在此基础上进行事故预测研究, 充分考虑了造成事故发生的众多因素, 尽可能的保留了事故发生前后的真实状态. 然而, 构建危化品事故状态向量需明确三个属性: 向量的维度、每个维度的形式、各维度之间的关系.
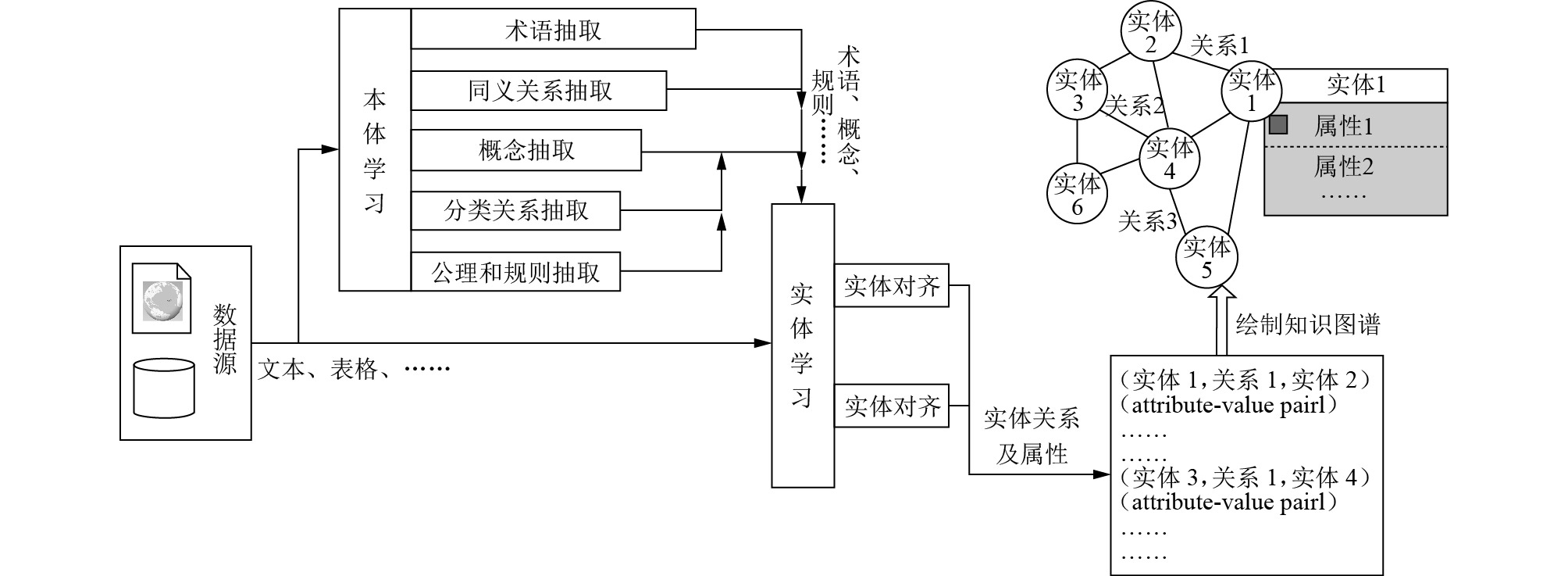
知识图谱是由节点和关系组成的图谱[10], 可直观的对危化品事故的场景进行建模, 运用“图”这种基础性、通用性的“语言”, “高保真”地表达事故因素之间的各种关系. 危化品知识图谱采用自顶向下和自底向上两种方式, 来提高实体抽取的准确度. 首先从数据源中获得本体、术语、顶层的概念以及相关规则, 然后不断地进行实体学习, 将新实体纳入前面的概念体系中. 同时, 从归纳实体开始, 进一步进行抽象, 逐步形成分层的概念体系, 如图2所示.
|
图 2 危化品知识图谱构建方法 |
智能信息搜索是从知识理解和逻辑推理的角度, 分析信息对象与检索请求的搜索方法[11]. 智能信息搜索在在于搜索过程和结果的智能化方面, 与传统搜索引擎的最大差别. 通过知识图谱等技术, 能够有效表达信息对象之间的联系, 充分理解用户的信息检索需求和信息对象包含的内容, 从而使得搜索引擎具备理解语义和有效推理的能力[12].
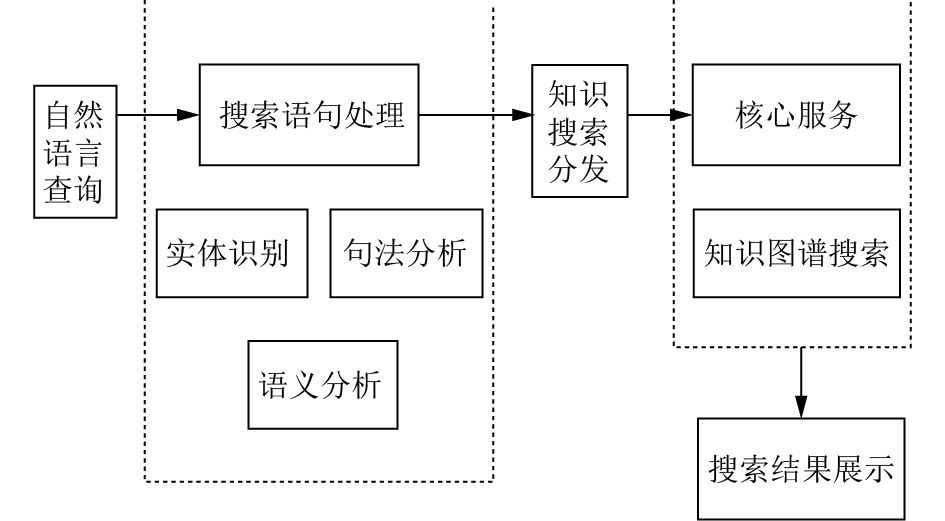
基于知识图谱的搜索服务是以危化品知识图谱作为底层的数据支持, 从用户的查询语句中抽取出实体和关系. 本文利用预定义模板的方法来处理基于知识图谱的搜索服务. 预定义模板基于实体、实体关系、实体属性将模板大致划分为三类: 实体模板、实体关系模板、实体属性模板. 在搜索语句处理模块中, 对查询语句进行实体、关系以及语法依存识别, 根据实体和模板能否构成知识图谱的一个子图, 选择匹配度最高的模板, 并将模板转换为对应的Cypher语句. 最终, 将用模板匹配得到的结构化查询语句提交至图数据库执行, 挖掘与危化品事故相关的所有关联因素, 如图3所示.
|
图 3 基于知识图谱的危化品事故关联因素搜索框架 |
2 基于状态向量的SVM事故预测方法
用向量来表示事故, 充分考虑了事故发生时的人为因素、物态因素、环境因素. 在事故状态向量基础上进行事故预测研究, 相比于传统的仅针对少数强关联因素(如死亡人数、事故发生起数等)建立的事故模型具有积极意义. 但事故状态向量带来的问题是事故的高维度, 以往针对少数强关联因素建立事故模型的方法已不适用, 由于支持向量机算法在高维度向量学习中表现出来的优势, 本文选其建立事故预测模型.
支持向量机(Support Vector Machines)是Vapnik等人提出的机器学习算法[13], 由于其出色的学习性能, 在人脸识别、手写识别、文本自动分类等很多领域都得到了成功应用[14].
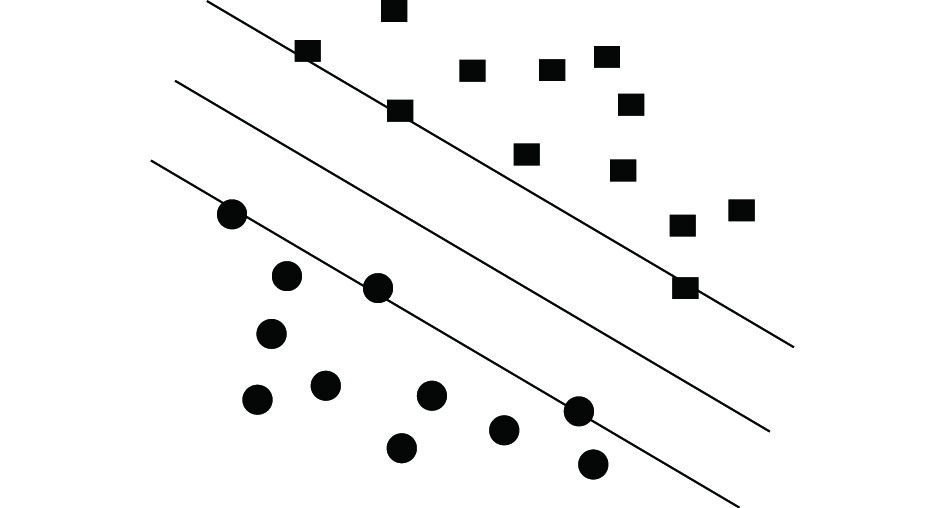
SVM具有直观的几何意义, 给定样本集{(xi, yi)| i=1, …,l; xi∈Rn yi∈{+1, − 1}}, 对于线性可分情况: 支持向量机目标就是寻找一个超平面<w, x> +b = 0将其正确分开, 这样的超平面往往不止一个, 其中与两类样本点间隔Margin最大的分类超平面会获得最佳的推广能力: 即最优分类超平面, 如图4所示. 最优超平面仅由离它最近的样本点所决定, 而与其它样本无关, 这些样本点即所谓的支持向量, 这也正是支持向量机名称的由来[15,16].
|
图 4 线性向量机 |
而对于非线性问题, 支持向量机采用特征映射方法, 通过引入核函数K, 使得:
| $ K\left( {xi,\;xj} \right) = \;\;\Phi \left( {xi} \right)\;\;\Phi \left( {xj} \right) $ |
实现非线性变化后的线性分类, 如图5所示.

|
图 5 非线性支持向量机 |
如果训练样本可以无误差地被划分, 每一类数据与超平面距离最近的向量与超平面之间的距离最大, 此超平面称为最优超平面. 求解最优超平面<w, x>+b=0, 即对于给定的训练样本, 找到权值ω和偏移b的最优值, 使下式最小化:
| $ \Phi \left( \omega \right) = 1/2\left| {\left| \omega \right|} \right|2 $ |
同时满足约束条件:
| $ yi\left[ { < \omega ,xi > + b} \right] \ge 1,i = 1, \cdots ,l $ |
可以看出这是一个二次规划问题[12], 采用拉格朗日乘子法求解, 引入拉格朗日乘子αi≥0, i=1, …, l, 求解下列函数:
| $max W(\alpha ) = \sum\limits_{i = 1}^l {{\alpha _i} - \dfrac{1}{2}\sum\limits_{i = 1,j = 1}^l {{\alpha _i}Q(i,j){\alpha _j}} } $ |
| $\sum\limits_{i = 1}^l {{y_i}{\alpha _i} = 0,\quad 0 \leqslant {\alpha _i} \leqslant C,\quad i = 1,\cdots,l} $ |
其中,
| ${\omega ^*} = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}} $ |
| ${b^*} = - \dfrac{1}{2} < {\omega ^*},{x_r} + {x_s} > $ |
| $f(x) = {sgn} ( < {\omega ^*},x > + {b^*}) = {sgn} \{ \sum\limits_{i = 1}^m {\alpha _i^*{y_i}K < x,{x_i} > + {b^*}\} } $ |
在利用SVM分类器进行分类时, 并非所有的样本都对分类起作用, 只有少量被称作支持向量的训练样本才起作用, 并且这些支持向量在几何位置上分布于超平面的周围[17]. 为了减少增量学习的样本数量, 应该尽可能选取那些可能成为支持向量的样本进行学习. 本文针对危化品行业数据特点, 提出了基于状态向量距离的SVM增量学习算法.
支持向量机增量学习问题可以描述如下: 存在历史样本集A, 增量样本集B, 并假定A与B满足A∩B=φ,
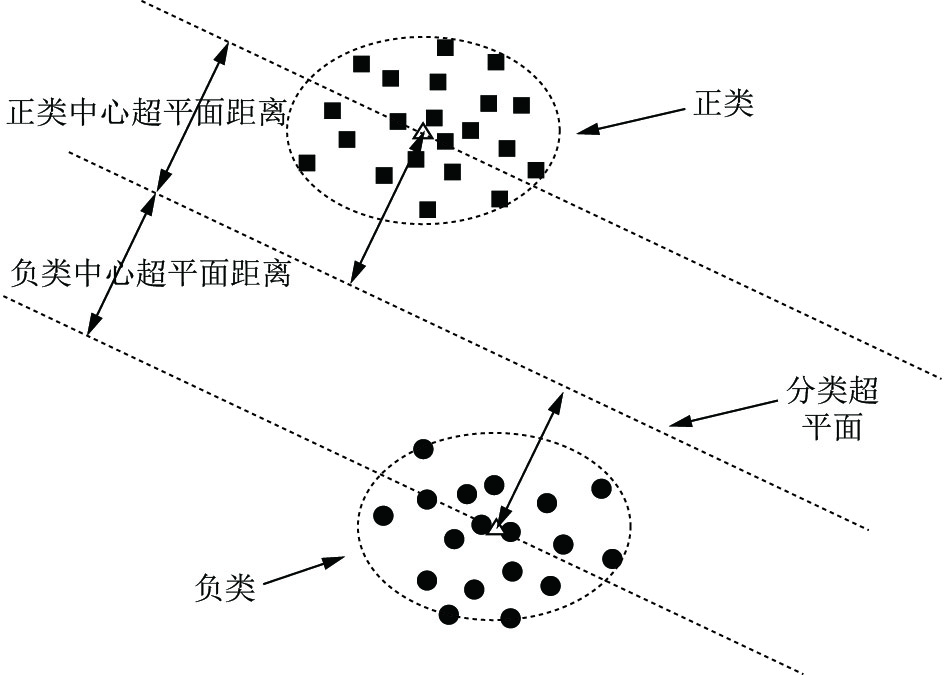
根据支持向量的几何分布特点, 判定一个样本是否能转化为支持向量应综合考虑以下两个因素: 一是这个样本到超平面的距离; 二是这个样本到该类样本中心的距离. 因此在进行增量学习时使用以下的筛选机制, 尽可能将可能成为支持向量的样本选到新训练集中. 用ASV表示原样本集中的支持向量, 在A-ASV中和BSV中都存在可能成为支持向量的样本. 从中选取靠近分类超平面且在类中心靠超平面侧的样本作为新增样本点. 如图6所示, 选取超平面距离小于中心平面距离的样本点组成边界样本集M. 将ASV∪BSV∪M作为最终的增量学习训练集.
|
图 6 边界样本集筛选机制示意图 |
经典SVM算法, 即非增量学习算法, 保留了所有训练样本点, 保证了预测分类的准确度, 但因为不支持增量学习, 全部重新训练, 由此造成的训练时间和训练迭代的样本个数较多, 降低了算法的效率. 传统增量学习算法[18]进行增量学习时, 认为增量样本中满足KKT条件的样本集对训练不起作用, 将其过滤, 仅将原始样本和新增样本中违反KKT条件的样本合并进行增量学习. 此方法有效的过滤了增量样本, 减少了训练样本的个数, 提高了训练时间, 但是由于筛选条件过于单一, 可能将对最优超平面起到支撑作用的支持向量进行过滤, 造成有效样本丢失, 由此降低预测分类的准确度.
三种算法从训练时间, 准确率两个方面进行比较如下:
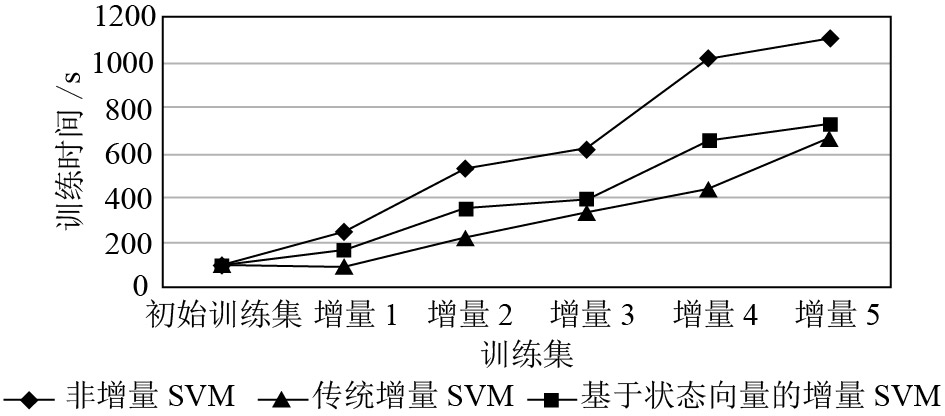
(1) 训练时间: 本文算法与经典SVM算法相比, 在训练时间上有大幅度的减少, 这是因为在增量学习过程中本文算法对新增样本和原有样本进行了有效的筛选, 在保留样本有效信息的前提下, 减少了训练样本的数量, 使增量学习的规模得到了良好的控制, 缩短了训练的时间. 但与传统增量学习算法相比, 在训练时间上略有劣势. 这是因为传统增量学习算法舍弃了原始样本中的非支持向量和新增样本的满足KKT条件的样本. 这种训练样本数量的减少是以牺牲样本有效信息为代价的, 最终将会影响到预测分类的准确率, 如图7所示.
|
图 7 算法训练时间比较 |
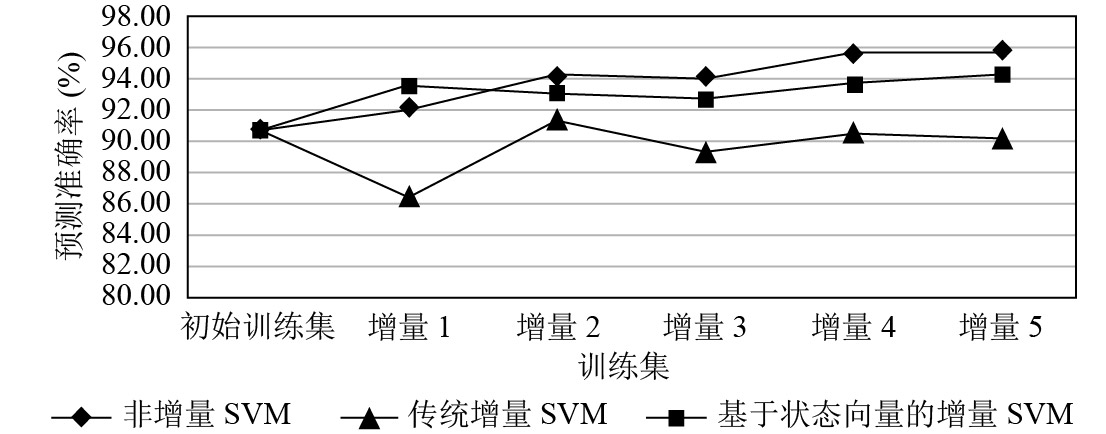
(2) 准确率: 本文算法的准确率仅次于经典SVM算法, 与传统的增量学习算法相比有大幅的提高. 非增量学习算法保留了原始样本和新增样本的全部信息, 因此预测准确率较高. 本文算法预测准确率仅次于非增量学习算法, 说明本文算法的筛选机制有效的保留了样本有效信息. 而传统增量学习算法因为舍弃了过多的样本点, 虽然增量学习的样本规模得到了有效的控制, 训练的时间得到了提高, 但是因为丢失了大量样本信息, 最终的预测准确率降低了, 如图8所示.
|
图 8 算法预测准确率比较 |
综合考虑以上两个方面的理论分析, 本文算法在训练时间和预测准确率等方面有较好的表现. 既弥补了经典SVM算法训练规模较大, 训练时间较长的缺陷, 又在一定程度上解决了传统增量学习算法丢失样本有效信息, 预测准确率偏低的问题.
3 基于状态向量的危化品事故预测应用分析 3.1 危化品事故状态向量构建针对目前掌握的619个典型危化品事故样例, 开展知识图谱分析, 构建事故状态向量. 通过实体学习, 针对从不同领域抽取到的知识, 建立有效的实体链接和知识合并方法, 消除信息中错误和冗余. 同时, 采用实体对齐方法实现不同知识图谱系统之间的链接与合并, 从而实现构建一个更大规模的危化品知识图谱系统, 构建的危化品知识图谱如图9所示.
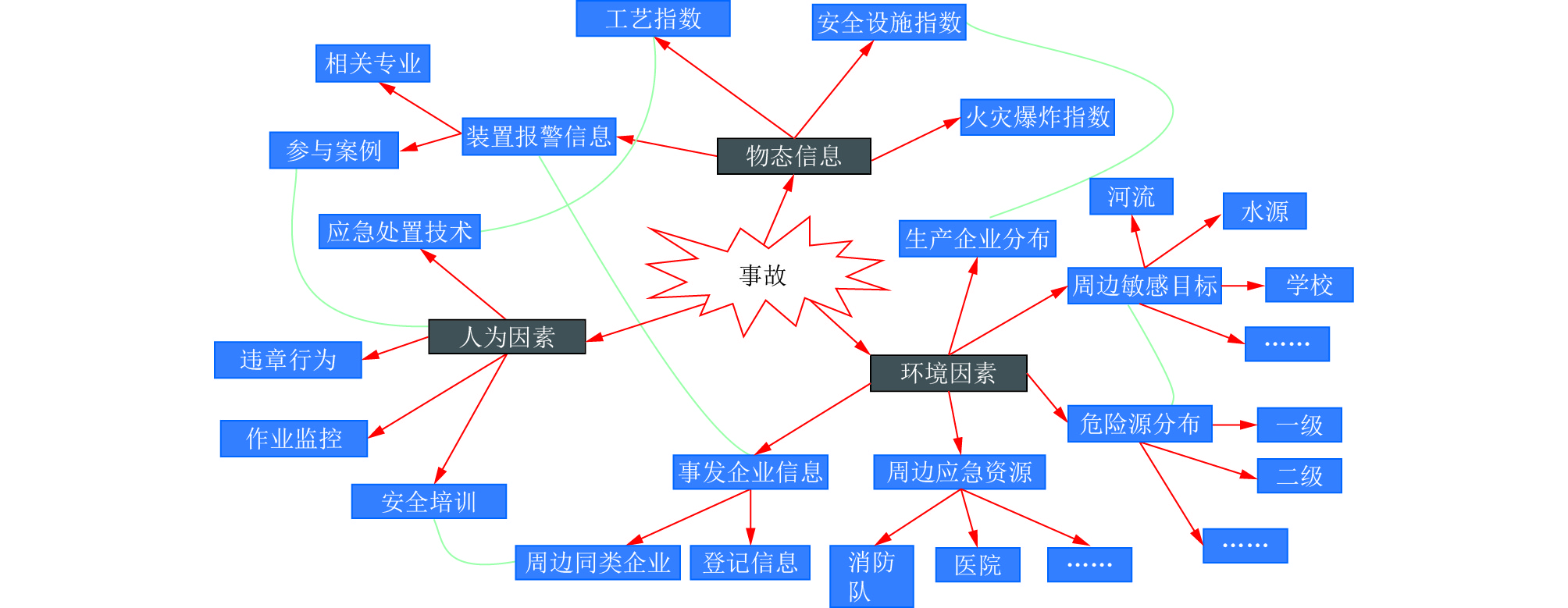
以火灾爆炸事故为例, 通过智能信息搜索提取相关因素, 按照人物环进行分类, 构建危化品事故状态向量, 共计265维. 其中, 人为向量P(维度185), 分为领导力与安全文化、工艺安全人为信息、过程安全人为控制、检查与绩效等几大类; 物态向量D(维度49), 分为危险物质的火灾、爆炸性指数、毒性指数、工艺指数、设备指数、安全设施指数等几大类; 环境向量E(维度31), 由气象指数和地理信息指数等组成, 如图10所示.

|
图 9 危化品知识图谱 |
|
图 10 危化品事故状态向量的知识图谱表 |
3.2 危化品事故预测方法验证
支持向量机可通过对事故向量的学习建立预测超平面, 并通过超平面对未知事故状态的向量做出预判, 从而形成事故预测模型, 具体算法如下:
(1) 收集事故状态信息. 危化品事故数据来自于化学品安全网(www.nrcc.org.cn), 共619个事故状态和1288个非事故状态.
(2) 标记事故状态. 其中事故状态为1, 非事故状态为−1;
(3) 将事故状态和非事故状态转化为向量形式, 事故状态向量的格式如下:
<label> <index1>: <value1> <index2>: <value2> … <indexn>: <valuen>
其中, label为事故状态结果, 1为事故状态, –1为非事故状态. index为特征维度, value为特征值, 其中n=265.
(4) 选取m=500个向量作为初始训练集Vt, 在剩余向量中随机选取900个组成3个集合V1,V2,V3, 作为测试集, 每个测试集样本数量300.
(5) 在训练集Vt上进行支持向量机训练学习, 构建预测超平面f(x).
(6) 利用预测超平面f(x)对测试集V1,V2,V3进行预测, 得出每个向量的预测结果
(7) 与测试集V1,V2,V3标记的原有事故状态进行对比, 鉴定预测结果.
(8) 修改Vt样本数量m的值, 重复步骤(5)~(8), 验证算法.
以上所有算法均在Matlab7.0和LibSvm-mat-3.20工具包[19]的基础上实现. 实验平台IBM3850服务器, CPU为4核E7-4830V2处理器, 内存16×16 GB DDR3, 操作系统为Windows server 2012. 实验中使用核函数为REF函数, C=1, 实验结果如表1–3所示.
| 表 1 SVM学习算法实验结果(m=500) |
| 表 2 SVM学习算法实验结果(m=750) |
| 表 3 SVM学习算法实验结果(m=1000) |
实验结果表明, 基于状态向量的SVM事故预测方法在保留了事故众多相关因素的同时, 可以有效的判断事故向量的状态, 预测结果准确率较高. 随着训练样本数量的不断增加, 预测准确率逐渐提升, 如图11所示.

|
图 11 预测准确率对比图 |
4 结论
本文从事故致因的理论角度, 分析了影响危化品事故发生的人为、物态和环境的复杂性因素,分析了危化品事故的形成机理, 指出传统的基于事件链事故分析不再适应于今天所建造的复杂系统, 并在此基础上给出了事故状态向量的定义, 提出了一种基于状态向量的危化品事故分析预测方法. 高维事故状态向量尽最大可能考虑了造成事故发生的众多因素, 利用支持向量机学习算法, 建立事故预测超平面, 以此对未知状态的向量进行预测. 通过样本实验表明, 本文提出的危化品事故预测方法, 预测准确率较高, 对危化品行业事故的预测预防具有积极意义. 随着危化品事故增量学习的不断进行, 危化品事故向量维度也会随之不断增加, 由此对本文基于状态向量的增量SVM学习算法在效率和训练时间方面提出更多要求, 在未来研究工作中, 将对向量维度筛选及算法效率提升等方面进一步深入研究.
| [1] |
任继勤, 穆咏雪. 危化品事故的统计分析与管理启示. 化工管理, 2015(16): 28-31. DOI:10.3969/j.issn.1008-4800.2015.16.012 |
| [2] |
国家安监总局化学品登记中心. 中国化学品安全网. http://accident.nrcc.com.cn, 2019.
|
| [3] |
安世宁. 安全生产" 十三五”规划八大要点. 中国安全生产, 2017(2): 13-14. |
| [4] |
肖兴志, 郭启光. 中国危化品安全事故频发之谜—基于佩尔兹曼效应视角. 财经问题研究, 2012(11): 31-38. DOI:10.3969/j.issn.1000-176X.2012.11.005 |
| [5] |
陈宝智, 吴敏. 事故致因理论与安全理念. 中国安全生产科学技术, 2008, 4(1): 42-46. |
| [6] |
Leveson N. Engineering a Safer World: SystemsThinking Applied to Safety. Cambridge: MIT Press, 2011.
|
| [7] |
Abdulkhaleq A, Wagner S. A software safety verification method based on system-theoretic process analysis. Bondavalli A, Ceccarelli A, Ortmeier F. Computer Safety, Reliability, and Security. Cham: Springer, 2014.
|
| [8] |
郑小平, 刘梦婷, 李伟. 事故预测方法研究述评. 安全与环境学报, 2008, 8(3): 162-169. DOI:10.3969/j.issn.1009-6094.2008.03.039 |
| [9] |
崔维, 刘士竹. 事故灾难类突发事件风险管理研究——以" 11•22”中石化东黄输油管道泄漏爆炸特大事故为例. 中国应急管理, 2014(6): 16-21. |
| [10] |
陈悦, 刘则渊, 陈劲, 等. 科学知识图谱的发展历程. 科学学研究, 2008, 26(3): 449-460. |
| [11] |
任利强, 郭强, 王海鹏, 等. 基于CiteSpace的人工智能文献大数据可视化分析. 计算机系统应用, 2018, 27(6): 18-26. |
| [12] |
姬源, 谢冬, 周思明, 等. 电力领域语义搜索系统的构建方法. 计算机系统应用, 2016, 25(4): 91-96. |
| [13] |
Vapnik V. The Nature of Statistical Learning Theory. New York: Springer, 1995.
|
| [14] |
Cristianini N, Taylor JS. An Introduction to Support Vector Machines and other Kerner-based Learning Methods. Cambridge: University Press, 2004.
|
| [15] |
萧嵘, 王继成, 孙正兴, 等. 一种SVM增量学习算法. 南京大学学报(自然科学版), 2002, 38(2): 152-157. DOI:10.3321/j.issn:0469-5097.2002.02.004 |
| [16] |
张灿淋, 姚明海, 童小龙, 等. 一种新的基于KKT条件的错误驱动SVM增量学习算法. 计算机系统应用, 2014, 23(1): 144-148. DOI:10.3969/j.issn.1003-3254.2014.01.028 |
| [17] |
Burges CJC. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167. DOI:10.1023/A:1009715923555 |
| [18] |
周伟达, 张莉, 焦李成. 支撑矢量机推广能力分析. 电子学报, 2001, 29(5): 590-594. DOI:10.3321/j.issn:0372-2112.2001.05.004 |
| [19] |
Chang CC, Lin C J. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 27. |
 2019, Vol. 28
2019, Vol. 28


