随着科学技术的发展, 虚拟现实(Virtual Reality, 简称VR)技术已经渗透进了军事生活的各个方面. VR技术因具有良好的可控性、安全性、费用低、不受气候影响、不受空间场地的限制等特点, 已被广泛应用到虚拟战场环境、军事训练等领域[1]. 如今将虚拟仿真技术应用在军队建设实用化方面受到越来越多的重视. 中国军队同样也无法避免军事虚拟仿真训练的国际化浪潮. 各国都面临国防预算削减、病理削减、同时要更加努力保持其有效性的要求. 中国军队在国际地位的崛起. 也面临着进入许多陌生国际地区进行军事防卫的任务. 这就迫切要求军事人员能够在他们可能不熟或难以进入的国家和气候条件下进行作战, 因此用虚拟仿真模拟的训练演练架构支持将是十分重要的. 现代战场作战方式的改变和科学技术的高速发展促使武器装备更新迭代周期加快, 随之增加的还有装备训练和演练的各种经费, 例如场地、装备、训练等费用. 新形式下, 针对创新装甲车辆等装备的训练方法, 大幅度降低日常训练成本、提高训练效率、增加训练灵活性和扩展性、提高训练安全性成为发展装备训练技术的需求驱动. 随着虚拟现实技术的高速发展, 采用智能传感器、三维建模、三维地理信息、粒子效果、沉浸式显示等技术手段能够逼真的建立虚拟的战场环境, 采用物理仿真可以仿真车辆的动力学特性, 从视觉场景和交互操作上完全模拟实装. 正是因为虚拟现实技术可以高度逼真的模拟人在自然环境中的视觉、听觉等行为, 真实的模拟环境多变的特点, 使得采用虚拟现实技术和物理仿真技术代替实装训练成为了一个非常重要的研究方向[2–4]. 装甲车辆的运动仿真目前已经有了许多的研究, 在文献[5]的研究中只是做了一个可视化的交互式的装甲车辆仿真系统, 文献[6]的研究中, 并未考虑不同地形对装甲车运动性能的影响. 在文献[7]中, 研究重点是装甲车在任意地形上的运动, 只是分析了装甲车的受力, 并未对装甲车自身姿态做进一步的研究. 文献[8]则将重点放在了场景和装甲车的建模上面. 以上研究皆未对装甲车在运动过程中自身姿态的问题做出更进一步的研究, 本文将针对在不同地形上, 装甲车自身姿态调整的相关问题进行研究.
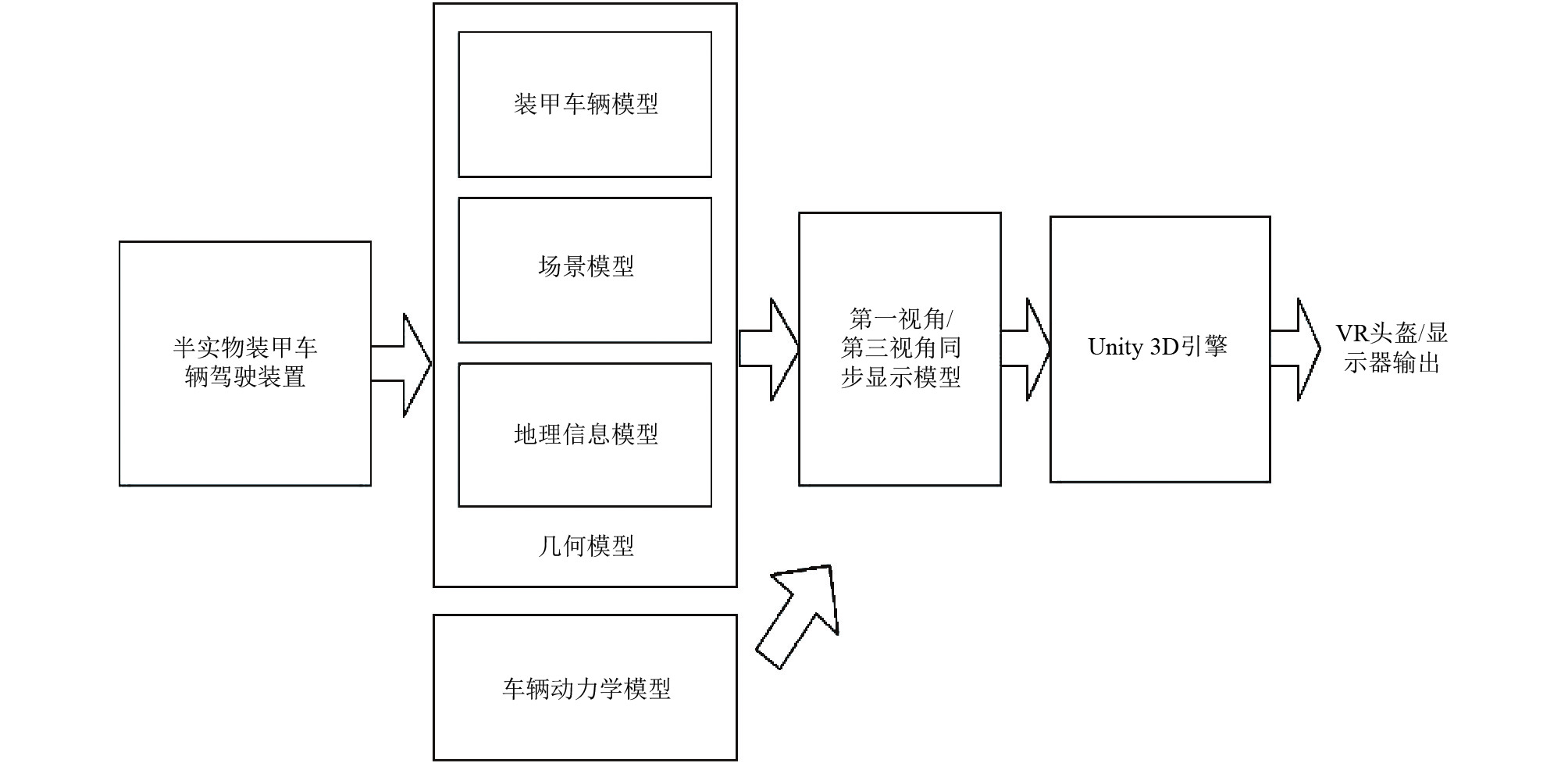
1 装甲车辆驾驶仿真模型建立了装甲车辆驾驶的仿真模型, 如图1所示.
|
图 1 装甲车辆驾驶仿真模型 |
模型分为半实物装甲车辆驾驶装置、几何模型、车辆动力学模型、第一视角/第三视角同步显示模型、Unity3D引擎和显示六部分. 半实物装甲车辆驾驶装置提供操作的输入信号, 包括操纵杆、油门、刹车和离合器等装置, 将输入信号作为几何建模的输入数据, 为几何建模提供数据上的支持. 几何模型包括车辆的实体模型、驾驶的场景模型(如城市、草原、山区等)、地理信息模型(包括高程数据和遥感影像). 车辆动力学模型用来计算车体的姿态. 在模型创建完成之后, 为使用者提供不同的视角. 第一视角/第三视角同步显示模型实现仿真过程中, 驾驶位第一视角和第三视角的同步显示. 通过Unity3D引擎将驾驶场景部署到VR沉浸式头盔. 以VR沉浸式头盔作为第一视角显示载体, 投影屏幕可作为第三视角显示载体.
1.1 装甲车辆实体模型构建在对当前最流行的几种建模工具软件进行详细对比后, 结合装甲车的特征和不同软件的优势特点, 使用了建模能力较强的3DMAX工具软件对装甲车进行初步的几何建模. 装甲车模型是由相对规则的组件构成的, 使用网格建模法, 采用一系列的阵列、放样、镜像、网格编辑、纹理材质等方法作为几何建模的辅助手段对模型进行外观上的优化, 最后将输出的数据导入到MultiGen Creator当中对模型进行详细的处理, 得到最终的装甲车侧模型. 输出的数据是由半实物装甲车辆驾驶装置提供的包括操纵杆、油门、刹车和离合器等装置的真实数据, 保证了模型的仿真[9–11].
图2是对装甲车实体模型的构建, 其中最重要的部分是对于履带模型的构建, 履带与一般的车轮不一样, 一般的车轮可以抽象成圆绕圆心旋转, 而履带却抽象成椭圆.

|
图 2 装甲车实体模型 |
履带实体建模如3图所示. 履带式装甲车在行进过程中自身重力有部分是由负重轮来承担, 并通过履带将自身重力作用于地面.前行运动通过模拟真实的发动机引擎, 转向运动是通过调整左右履带的速度来实现的.装甲车辆模型可由模拟驾驶舱来操控, 也可以使用手柄操控.

|
图 3 履带模型图 |
1.2 装甲车辆运动过程动力学建模
对装甲车辆运动过程进行动力学建模, 主要分析其受力, 运动形态[12].
1.2.1 受力分析装甲车辆在与地平面成α角的斜坡上行驶, 受到的主要力有自身重力、空气阻力、地面阻力以及引擎的牵引力.
1) 重力
重力是由装甲车自身重量决定的, 假设装甲车辆是左右对称的, 其重心在其纵对称面上.
2) 空气阻力Rk
计算公式可表示为:
| $ {R_k} = CA{v^2} $ | (1) |
其中: A表示坦克的正投影面积, 假设在理想环境中, 装甲车在前行过程中只会受到迎面而来的风.C是空气阻力系数.v是装甲车行驶的速度. A表示的就是受到风吹的面积, 其计算公式表示为:
| $ A = mWH $ | (2) |
W是履带的中心距, H是高度, m是修正系数, v是装甲车行驶速度.
3) 地面阻力
由于装甲车体积大, 重量大, 履带与地面接触面积大的原因, 装甲车在经过时, 地面会下陷从而对装甲车有一个向上的反作用力, 在离开某段地面时, 又会给装甲车一个前行的牵引力, 再加上地面的摩擦力.再加上路况的原因, 装甲车可能会发生打滑的现象. 这些原因使得地面阻力的分析变得十分复杂.根据以上分析, 考虑到实际需求, 对地面阻力进行了以下简化: ①地面不会因装甲车的重量而下陷. ②装甲车在前行过程中的地面附着力要大于牵引力, 不会出现打滑的现象. ③装甲车在转弯的时候不会产生侧滑. 简化后的地面阻力公式可表示为:
| $ {\rm{R}} = {\mu _\gamma }Q $ | (3) |
其中, μγ是装甲车行驶过程中地面变形阻力的系数, Q是装假车对地面的附着重力.
4) 牵引力
牵引力分为装甲车引擎的动力和经过某段路后, 土壤给装甲车的牵引力. 在这里要求不是很高, 土壤给装甲车的牵引力可以忽略不计. 只考虑装甲车引擎的牵引力就足够了. 装甲车牵引力F的计算公式可表示为:
| $ F = \frac{{{M_f}i\eta }}{{{r_z}}} $ | (4) |
其中, Mf表示发动机扭矩, rz表示主动轮半径, i表示某档的总传动比, η表示装甲车的效率.
1.2.2 运动形态分析装甲车的运动形态主要分为直线行驶状态和转弯状态. 为了保证装甲车在行驶过程中不会出现嵌入地里和悬空的情况, 还要及时对装甲车的姿态进行调整. 装甲车的行驶有六个自由度, 前后、左右和上下三个移动自由度, 翻滚、偏航和俯仰三个旋转自由度. 通过移动自由度确定装甲车的位置, 通过旋转自由度来调整装甲车的姿态.
1) 直线行驶状态
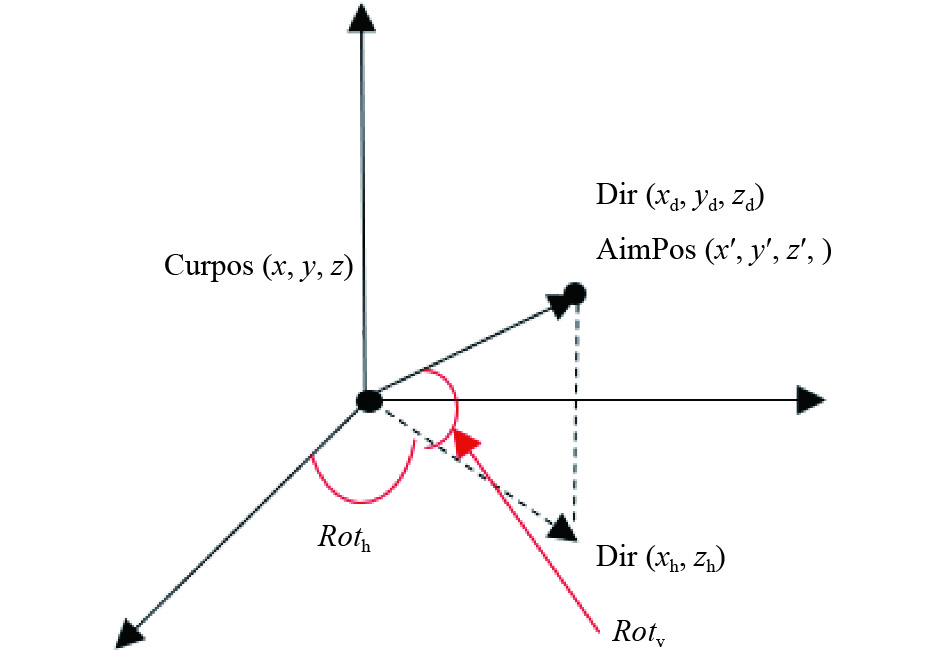
以有一定坡度的上坡路为例, 装甲车在上坡路上直线行驶的过程中速度为v, 假设当前所处的位置为 CurPos(x, y, z), 目标位置是AimPos(x’, y’, z’), 移动方向为Dir(xd, yd, zd), 垂直偏转角度(移动方向与水平面的夹角)为Rotv, 水平偏转角度Roth, 移动方向在水平面上的投影为: Dir(xh, zh), 如图4.
|
图 4 直线行驶状态图 |
由图4可以得出:
垂直偏转角度
| $ Ro{{t}_{v}}=\arcsin ({{{y}_{d}}}/{v\Delta t}\;) $ | (5) |
水平偏转角度
| $ Ro{{t}_{h}}=\arctan ({{{z}_{d}}}/{{{x}_{d}}}\;) $ | (6) |
目标位置的坐标为:
| $ \left\{ \begin{align} & {x}'=x+v\Delta \cos Ro{{t}_{h}}*\cos Ro{{t}_{v}} \\ & {y}'=y+v\Delta t\sin Ro{{t}_{h}} \\ & {z}'=z+v\Delta \cos Ro{{t}_{h}}*\sin Ro{{t}_{v}} \\ \end{align} \right. $ | (7) |
其中Δt是时间的变化量.
装甲车姿态的调整
在简单的上坡、下坡行驶中, 需要调整俯仰自由度. 如果不调整, 装甲车在上坡的过程中会出现嵌入地面的情况, 下坡的时候会出现悬空的情况.
如图5取装甲车两边履带所在的平面与水平面的夹角为俯仰角, 实时调整俯仰角保证两边履带所在平面与接触地面的法向量垂直. 通过这种方法调整装甲车的姿态. (利用装甲车行驶的方向向量所在的垂直于水平面的面将地形切出一个平面).

|
图 5 装甲车俯仰角 |
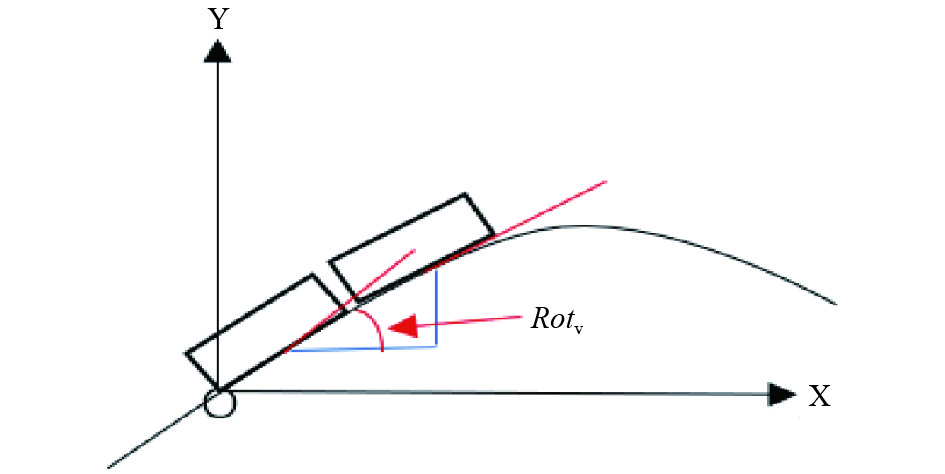
如图6所示, 将装甲车的运动投影到XOY平面上, 则装甲车在某点上的俯仰角等于曲线在该点的斜率.
|
图 6 装甲车调整俯仰角 |
2) 转弯行驶状态
装甲车因为履带的关系使其与一般车辆的转弯行驶有所不同. 在文献[1]中介绍了有关履带车辆的转向运动. 当履带车辆以速度v做半径为R的转向运动时, 分为大半径区和小半径区两种情况
① 小半径区就是指转弯半径的取值范围[0, W/2]之间, 其中W是车身的宽度, 也就意味着旋转中心在装甲车内部. 此时装甲车两侧的履带的速度的方向是相反的, 模拟这种情况可以简化为给装甲车一个固定的角速度, 让装甲车绕质心所在的法向量做旋转运动, 即原地打转.
② 大半径区是指转弯半径大于W/2. 此时装甲车转弯的形态就像一般的车辆. 即使是这样, 装甲车辆的转向行驶状态也是十分复杂的. 假定装甲车是在水平面上运动, 但是装甲车在高速转弯和低速转弯时所受到的离心力影响是不同的, 转向阻力矩也是不同的. 若是把装甲车看成是刚体, 则它应该有六个自由度: 横向、纵向、垂直三个平移自由度, 翻滚、俯仰、和偏航三个旋转自由度. 由于是在水平面做转向运动, 就没有垂直方向的平移自由度和翻滚、俯仰两个旋转自由度. 只剩横向、纵向两个平移自由度和偏航一个旋转自由度. 为了简化设计的复杂性, 不考虑离心力和转向阻力矩, 只考虑装甲车以速度v进行转向(以左转为例)行驶. 为了方便观察, 以俯视的角度绘制示意图. 其中Center(x0, y0)是装甲车转弯轨迹圆的圆心, CurPos(x, z)是装甲车的当前所处的位置, Dir(xd, zd)是当前的行驶方向, AimPos(x’, z’)是装甲车目标位置, Dir’(xd’, zd’)是装甲车到达目标位置时的行驶方向.
如图7所示, 可求得两点之间的弧长(即装甲车的运动轨迹的长度)为vΔt, 两点之间的距离(即弧对应的弦长)为
| $ v\Delta t={\rm{R}\theta }/{2}\; $ | (8) |
| $ \sqrt{{{({{x}^{'}}-x)}^{2}}+{{({{z}^{'}}-z)}^{2}}}=2R\sin ({\theta }/{2}\;) $ | (9) |
在水平面上的转弯不需要进行姿态上的调整.

|
图 7 水平地面转弯 |
3) 比较复杂的情况是在坡路上转弯
装甲车在坡路上转弯, 会涉及到俯仰、偏航和翻滚三个自由度的变化. 取装甲车两边履带所在平面的方向向量的方向为装甲车的速度方向. 假定装甲车在上坡路上向左转弯俯仰自由度在减小的同时, 翻滚自由度在增大(右履带要比左履带高). 两者的改变量是相同的, 所以翻滚自由度是不需要考虑的. 在已知装甲车行驶速度的前提下, 讨论偏航角和俯仰角之间的关系.
如图8所示A是开始转向时速度的方向, A’是A在地面上的投影, B是转向后的方向, B’是B在地面上的投影.∠AOA’是开始转向时的俯仰角∠BOB’是转向后的俯仰角, ∠A’OB’是偏航角, 可以得到俯仰角和偏航角之间的关系为:
| $ \angle { B}{ O}{ B}' = \angle { A}{ O}{ B} * \angle { A}{ O}{ A}'/{90^ \circ } $ | (10) |
装甲车的受力和地形是影响其自身姿态的最主要原因, 自身姿态的改变体现在俯仰角、翻滚角、偏航角的变化. 通过对装甲车在不同地形上的受力分析以及装甲车的当前状态, 利用公式计算出俯仰角、翻滚角、偏航角的变化, 从而达到调整自身姿态的目的.

|
图 8 坡道转弯 |
1.3 地形场景构建以及驾驶视角
为了尽可能的模拟真实的装甲车的行驶环境, 检验装甲车辆运动姿态与虚拟地形表面的契合度, 本系统选取某靶场的真实地形作为虚拟训练场景的地形来源. 采用靶场真实地形的DEM数据作为真实地形环境生成的依据, 同时从该靶场航拍影像数据中提取地形的真实纹理数据, 动态铺设虚拟环境的地形表面纹理, 有效避免了遥感影像贴图随缩放而发生失真现象的产生.
驾驶者可以从第一视角和第三视角去观察装甲车的运动形态和自身姿态.

|
图 9 第一视角图 |
使用Unity3D引擎在装甲车模型内部放置摄像机, 方向是装甲车的正前方, 该摄像机的视野就是第一视角的视野.
使用Unity3D引擎在距离装甲车中心一定距离处放置摄像机, 该摄像机可以在以装甲车中心为圆心, 以距离为半径的球面上运动, 方向始终朝向装甲车, 该摄像机的视野就是第三视角的视野.

|
图 10 第三视角图 |
2 试验与分析
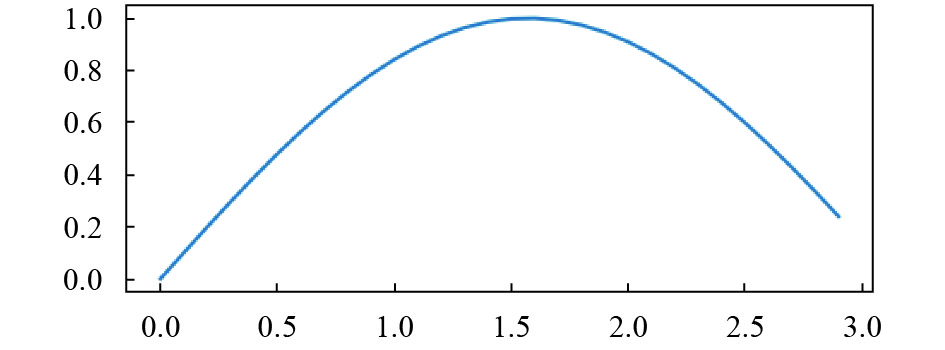
利用Python绘制如下坡道, 在这个坡道上实验计算装甲车行驶时模型的可行性.
装甲车在坡道上做直线行驶时, 俯仰角和车辆位置之间的关系
| 表 1 坡道直行, 位置与俯仰角的关系 |
利用图11中的坡道作为装甲车坡道转弯时的模型.假定装甲车的初始位置是0.9, 装甲车左转行驶, 其偏航角、俯仰角和翻滚角之间的关系.
|
图 11 坡道模型图 |
采用上述算法对装甲车自身姿态进行调整结果如下:
在装甲车运动的过程中, 如果不能对装甲车自身的姿态做出及时的调整, 会出现装甲车悬空或嵌入地面的情况, 本文通过对装甲车受力分析以及对装甲车当前速度、位置等信息的分析, 进而对影响装甲车自身姿态的三个变量进行计算, 达到调整装甲车自身姿态的目的.可以看到在这三种形态下, 装甲车自身的姿态都能随着地形的起伏变化做出相应的调整, 使得装甲车的履带紧贴地面.
| 表 2 坡道转弯, 偏航角、俯仰角与翻滚角之间的关系 |

|
图 12 直行上坡图 |

|
图 13 坡道左转图(上坡) |

|
图 14 坡道左转图(下坡) |
3 结论
在装甲车辆模拟驾驶仿真中, 实时调整装甲车的姿态是重要组成部分. 通过分析地形特点和装甲车运动的动力学模型本文给出了装甲车在坡道上直线行驶和转弯行驶的模型, 通过对模型的仿真和数据的分析验证了模型的可行性. 本文对三维地形下装甲车的运动姿态做了数据分析, 后续将研究不同地形下装甲车的运动所带来的触感进行深入研究.
| [1] |
陈定方, 罗亚波. 虚拟设计. 北京: 机械工业出版社, 2002. 1–2.
|
| [2] |
王艾萍, 范士海, 王润岗. 装甲车辆运动姿态实时仿真系统设计与实现. 火力指挥控制, 2013, 38(8): 111-114, 118. |
| [3] |
蒋庆全. 虚拟现实技术的军事应用. 现代防御技术, 2001, 29(2): 44-49. DOI:10.3969/j.issn.1009-086X.2001.02.011 |
| [4] |
万刚, 夏青, 武志强. 虚拟视景仿真中实体行为建模技术的研究. 测绘学院学报, 2002, 19(3): 214-216. DOI:10.3969/j.issn.1673-6338.2002.03.018 |
| [5] |
彭晓军, 史美萍, 贺汉根. 虚拟环境中装甲车辆运动仿真的研究. 计算机仿真, 2004, 21(2): 28-31. DOI:10.3969/j.issn.1006-9348.2004.02.009 |
| [6] |
欧阳冠军, 范晋伟, 王宇心, 等. 虚拟视景中的装甲车辆运动仿真算法研究. 计算机仿真, 2007, 24(12): 94-96, 104. DOI:10.3969/j.issn.1006-9348.2007.12.025 |
| [7] |
李东. 虚拟环境中装甲车辆运动仿真的研究. 华人时刊, 2014(6): 170. DOI:10.3969/j.issn.1006-0278.2014.06.131 |
| [8] |
黄高, 王宇, 王思维. 装甲车虚拟现实驾驶训练系统技术的研究. 军民两用技术与产品, 2016(8): 62. DOI:10.3969/j.issn.1009-8119.2016.08.060 |
| [9] |
冯广斌, 侯玉杰, 孙华刚. 装甲车传动装置换挡缓冲调压仿真. 计算机仿真, 2018, 35(11): 7-11. DOI:10.3969/j.issn.1006-9348.2018.11.004 |
| [10] |
应小昆, 杜增辉, 曲强, 等. 装甲车三维装配工艺设计与仿真及现场可视化技术. 新技术新工艺, 2017(12): 71-77. |
| [11] |
孙伟, 赵耀, 刘林. 无人履带装甲车双流传动系统研究计算与仿真. 机械工程师, 2015(10): 24-26. DOI:10.3969/j.issn.1002-2333.2015.10.013 |
| [12] |
梅尔霍夫W, 哈克巴尔E M. 履带车辆行驶力学. 韩雪梅, 译. 北京: 国防工业出版社, 1989.
|
 2019, Vol. 28
2019, Vol. 28


