随着社会的高速发展, 越来越多的车辆出现在人们的日常生活中, 给人们带来一定程度出行便利的同时, 也导致了城市交通的日益拥堵. 城市短时交通流预测作为城市计算[1–3]中的一个重要研究方向, 由城市交通大数据驱动, 可以大大提高生活效率, 提升城市的智能化水平.
短时交通流预测的研究已经发展了很多年, 从统计学方法到神经网络方法和模糊系统的方法, 交通流预测越来越精确、适用. 统计学方法是通过对历史交通流数据进行线性回归处理来进行交通流预测的. Sun等[4]利用局部线性回归模型对从休斯顿采集到的交通流数据进行短时预测. Dang等[5]采用多元线性自回归模型进行交通流预测. Williams等[6,7]根据季节性自回归移动平均(ARIMA)算法建模以便交通流预测. Tan等[8]将ARIMA模型和支持向量机(SVM)模型结合组成混合模型来预测交通流. 作为样本学习的优势方法, 支持向量机在交通流预测中也有很多应用. 朱征宇等[9]把卡尔曼滤波和SVM结合起来, 发挥两者的优势来共同预测短时交通流. 文献[10]中提出了一种将支持向量回归(SVR)模型用到交通流预测上的方法, 进而应用到动态导航系统上. 文献[11]运用SVR和连续蚁群算法对城市间交通流量进行了预测. 神经网络方法由于其高效的学习能力, 在交通流预测中得到了越来越多的应用. Kim等人[12]结合混合高斯和神经网络方法建模, 结合道路和环境因素进行交通流预测. 文献[13]中通过利用深信度神经网络(DBN)的方法建模来预测交通流. 文献[14]中将卷积神经网络(CNN)和SVR结合起来组成预测交通流的混合模型. 但上述方法其模型不具有可解释性, 近年来以规则刻划的模糊方法在交通流预测中得到发展, 特别是和神经网络有机结合的模糊神经网络方法. Yin等[15]结合了模糊系统和神经网络提出一种模糊神经模型来预测街道交通流. Quek等[16]利用模糊神经网络模型来预测交通流, 这种模型结合了模糊推理系统和神经网络, 互补的利用两者的特点来预测. Chan等[17]根据模糊神经网络和Taguchi方法相对高精度的预测道路交通流数据.
上述研究中采用了各种各样的模型来预测交通流, 可以看出对于交通流特征学习的改进方法层出不穷, 但是关于交通流数据的固有特性却一直未能很好的利用. 通过观察交通流的数据, 可以发现一些关于交通流周期性的先验知识, 如不同工作日的交通流具有相似的趋势, 即交通流量具有周期性模式. 交通流的周期性是城市交通数据的重要特征, 可以很好的反应出城市交通流量的特点, 利用这种先验知识训练交通流预测模型, 可以提高模型的预测性能. 本文将交通流的周期性先验知识提取出来, 获得交通流残差数据, 进而通过残差数据训练混合模型得到交通流预测值, 通过跟BPNN模型和普通ANFIS模型进行对比, 验证混合模型的优越性. 本方法利用ANFIS结合交通流周期性的混合模型来预测短时交通流, 即可以充分利用交通流的特性, 也可以发挥ANFIS适应交通流非线性数据的特点, 可以准确的预测城市短时交通流量. 该研究基于实际城市交通流数据来验证混合模型的泛化能力, 为接下来在其他应用方面的研究提供全新的思路.
1 方法介绍为了证明混合模型在交通流预测中的优越性, 本文用了混合模型跟BPNN模型和普通ANFIS模型相比较, ANFIS模型和BPNN模型具体内容如下:
1.1 ANFIS模型自适应模糊推理系统(ANFIS)是由Jang[18]首次提出的, 它有机结合了模糊推理系统(FIS)和神经网络(NN), 利用神经网络的框架, 通过自适应的混合算法在数据中提取模糊规则, 进而调整前件参数和后件参数, 获取最优解, 既发挥了FIS和NN的优点, 又弥补了彼此的不足, 增强了FIS的学习能力. 假定采用规则库:
| $ \begin{split} &\Big\{ {R\left( s \right):{x_1} = D_1^s,{x_2} = D_2^s, \cdots ,}\\ &{{x_n} = D_n^s \to {y_s}\left( {x} \right) = c_0^s + \sum\limits_{i = 1}^n {c_i^s{x_i}} } \Big\}_{s = 1'}^S \end{split} $ | (1) |
其中,
对应该规则库的ANFIS结构如图1所示. 该ANFIS一共有5层, 第一层为模糊化层, 将输入数据
上述ANFIS输入输出关系可以描述为:
| $\hat y\left({ x} \right) = \displaystyle\sum\limits_{s = 1}^S {{{\bar f}_s}\left({ x} \right){y_s}\left({ x} \right)} = \dfrac{{\displaystyle\sum\nolimits_{s = 1}^S {{f_s}\left({ x} \right){y_s}\left({ x} \right)} }}{{\displaystyle\sum\nolimits_{s = 1}^S {{f_s}\left({ x} \right)} }}$ | (2) |
其中,
| ${f_s}\left({ x} \right) = \prod\limits_{j = 1}^n {{\mu _{D_j^s}}\left( {{x_j}} \right)} $ | (3) |
| ${\bar f_s}\left({ x} \right) = \dfrac{{{f_s}\left({ x} \right)}}{{\displaystyle\sum\nolimits_{s = 1}^S {{f_s}\left({ x} \right)} }}$ | (4) |
ANFIS模型的构建过程, 首先确定输入数据的模糊划分和模糊集合类型, 然后采用反向传播算法和线性最小二乘法的混合算法进行前件参数和后件参数的训练, 前件参数采用反向传播算法进行训练, 后件参数运用最小二乘法进行训练. 输入数据沿ANFIS网络运算到第四层, 固定前件参数, 用最小二乘法训练后件参数, 信号正向传递至输出层, 利用反向传播算法训练前件参数, 循环迭代至全局最优.

|
图 1 ANFIS结构图 |
1.2 BPNN模型
BPNN是迄今应用范围最广泛的人工神经网络之一, 理论上具有无限逼近的能力, 在BPNN中, 通常采用反向传播算法或其变种来确定整个网络的权重. 在本文中考虑一个具有
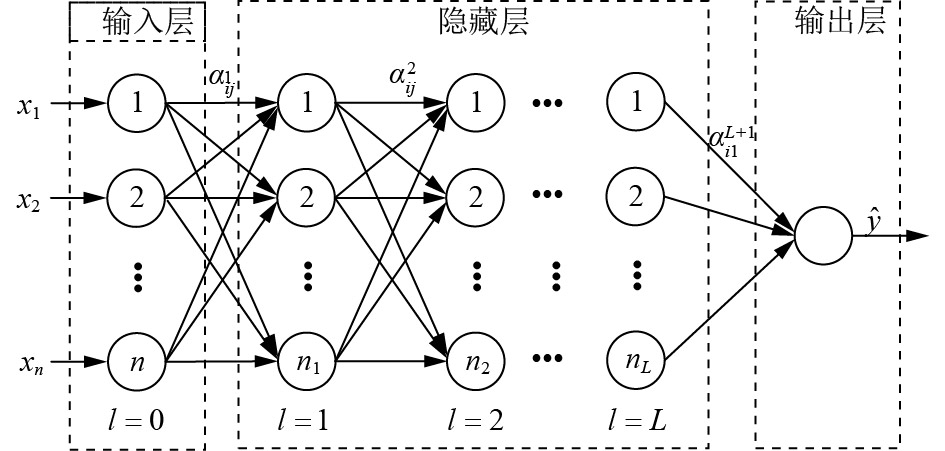
|
图 2 BPNN结构图 |
BPNN的输入输出关系可以表示为:
| $\hat y(x) = f\left(\sum\limits_{s = 1}^{{n_L}} {\alpha _{s1}^{L + 1} \cdots f\left(\sum\limits_{j = 1}^{{n_1}} {\alpha _{jl}^2f\left(\sum\limits_{i = 1}^n {\alpha _{ij}^1{x_i}} \right)} \right)} \right)$ | (5) |
其中,
BP算法会通过最小化平方差公式来获得最优值或者次优值, 如下式所示:
| $E(k) = {(\hat y({x^{(k)}}) - {y^{(k)}})^2}$ | (6) |
其中,
在BPNN算法中, 连接权重
| $\alpha _{ij}^l(k + 1) = \alpha _{ij}^l(k) - \varepsilon \frac{{\partial E(k)}}{{\partial \alpha _{ij}^l}}$ | (7) |
其中,
结合上述ANFIS模型和周期性提取方法, 本文提出了一个基于ANFIS混合模型的交通流预测模型. 结构如图3所示.

|
图 3 交通流ANFIS模型 |
模型训练的步骤如下:
1) 提取交通流数据周期性信息, 从交通数据中移除提取的周期性信息, 获得交通流残差数据.
2) 将交通流残差数据输入混合模型, 利用混合训练方法训练前件、后件参数以取得最优结果.
3) 将训练完的交通流残差数据和交通流周期性信息重新结合, 得到最优交通流预测值.
2.2 周期性知识模型构建假设有M天历史交通流数据
| $\left\{\begin{array}{*{20}{c}} {{Y_1} = [{y_1}(1),{y_1}(2), \cdots ,{y_1}(T)]}\\ \vdots \\ {{Y_M} = [{y_M}(1),{y_M}(2), \cdots ,{y_M}(T)]} \end{array} \right.$ | (8) |
对于每天一个周期的周期性信息, 提取的方法为:
| ${\bar Y_{\rm{Ave}}} = [\frac{1}{M}\sum\limits_{z = 1}^M {{y_z}(1)} ,\frac{1}{M}\sum\limits_{z = 1}^M {{y_z}(2)} , \cdots ,\frac{1}{M}\sum\limits_{z = 1}^M {{y_z}(T)} ]$ | (9) |
然后, 残差数据可以表示为:
| ${Y_{{\rm{Res}}}} = \{ {Y_1} - {\bar Y_{\rm{Ave}}},{Y_2} - {\bar Y_{\rm{Ave}}}, \cdots ,{Y_M} - {\bar Y_{\rm{Ave}}}\} $ | (10) |
这个部分主要介绍利用混合模型进行交通流预测实验的细节和过程.
3.1 实验数据本文选用2009年10月1号到2009年11月30号的交通流数据用来训练和测试, 实验数据来源于PeMS(美国加州性能测量系统), 数据通过探测器每30秒收集一次. 本文用10分钟、15分钟的时间间隔进行交通流预测实验, 用来验证模型的性能. 初始数据如图4所示.
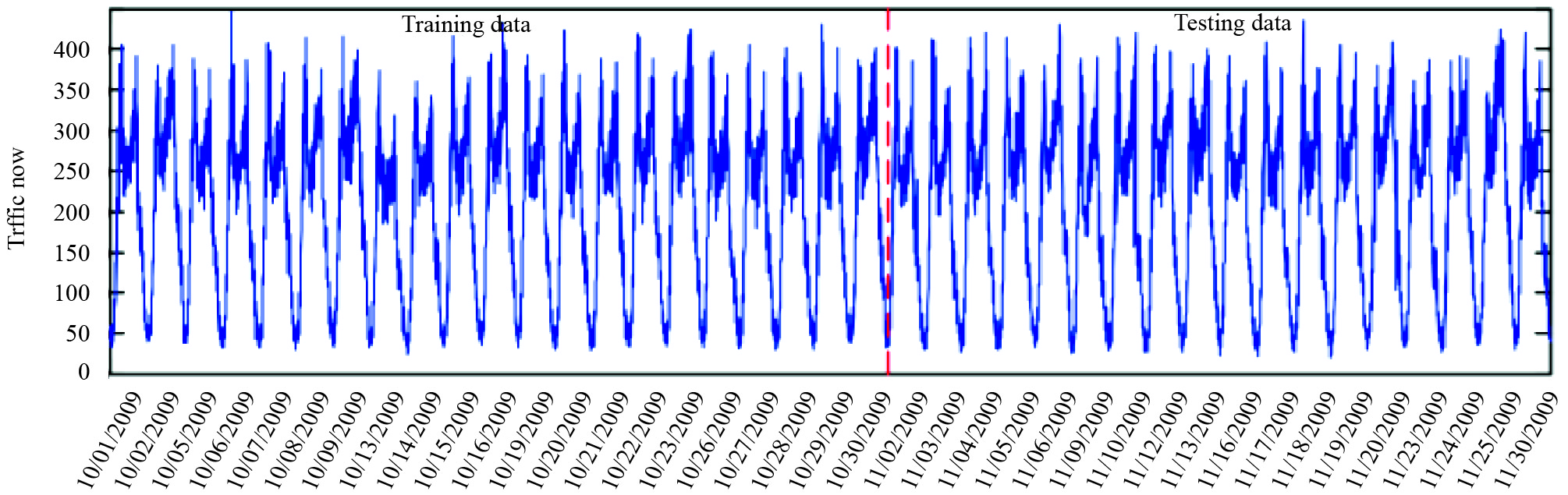
|
图 4 原始交通流数据图 |
3.2 性能指标
模型的预测性能用均方根误差(RMSE)、平均绝对误差(MAE)、平均百分比误差(APE)三个指标来衡量, 具体如下:
| $\left\{\begin{split} &{\rm{RMSE = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left| {\hat y({{{x}}^i}) - {y^{(i)}}} \right|}^2}} } , \\ & {\rm{MAE = }}\frac{1}{N}\sum\limits_{i = 1}^N {\left| {\hat y({{{x}}^i}) - {y^{(i)}}} \right|} , \\ & {\rm{APE = }}\frac{1}{N}\sum\limits_{i = 1}^N {\frac{{\left| {\hat y({{{x}}^i}) - {y^{(i)}}} \right|}}{{\left| {{y^{(i)}}} \right|}}} \times 100\% , \end{split}\right. $ | (11) |
其中,
本文采用的交通流实验数据总共有39天, 前21天的数据作为训练数据, 余下18天的数据作为测试数据, 交通流数据每天有144个10分钟间隔的数据点, 所以训练数据有21×144=3024个, 测试数据有18×144=2592个, 如图5(a)所示, 周期性数据如图5(b)所示, 去除周期性的残差数据如图5(c).
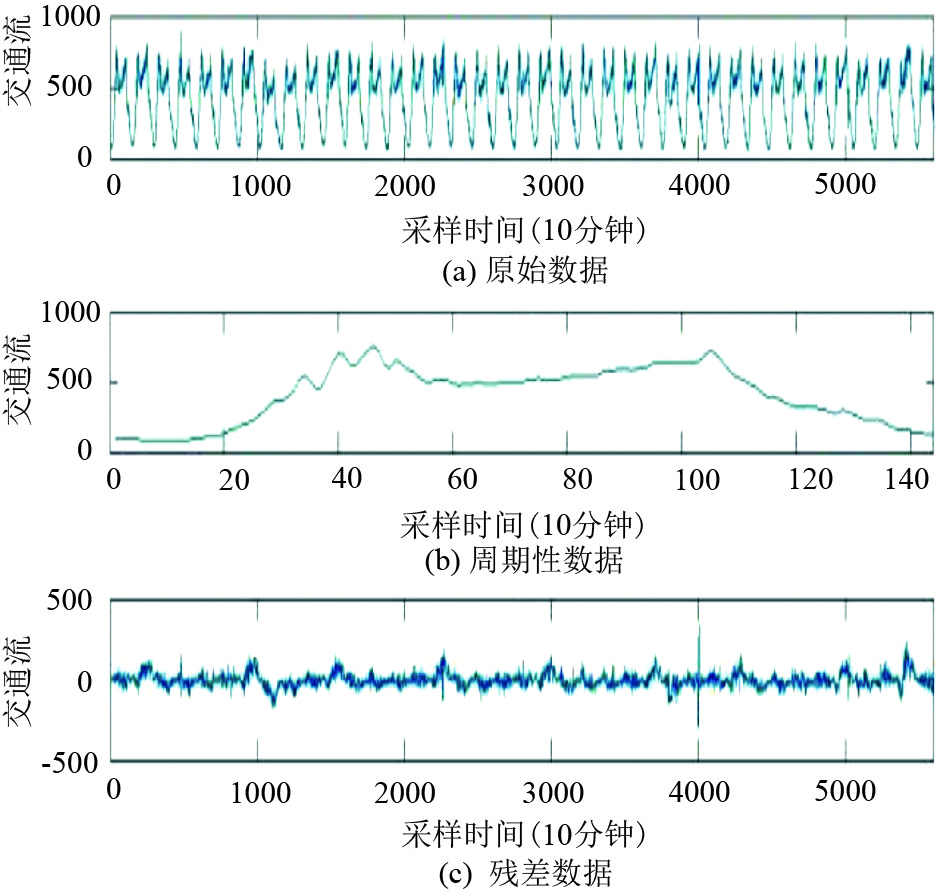
|
图 5 交通流数据(10分钟间隔) |
利用残差数据训练混合ANFIS模型, 预测结果(10分钟间隔)如图6所示.

|
图 6 交通流预测结果(10分钟间隔) |
混合模型和其他交通流预测模型的实验(10分钟间隔), 各指标对比如表1所示.
| 表 1 不同模型的指标对比(10分钟间隔) |
3.3.2 交通流预测(15分钟间隔)
15分钟间隔的交通流预测, 交通流训练数据有2016个点, 1728个测试点, 原始数据如图7(a)所示, 周期性数据如图7(b), 残差数据如图7(c).
将残差数据用来训练本文提出的混合交通流预测模型, 预测结果如图8所示.
混合模型15分钟时间间隔的交通流预测与ANFIS模型和BPNN模型的预测指标对比如表2所示.
交通流数据和二次交通流预测实验的预测值散点图如图9所示.
3.4 实验结果分析从上述两个不同时间间隔的交通流预测实验中可以得到以下结论:
1) RMSE、MAE、APE三个性能衡量参数越小, 证明模型的预测性能越好. 从表1和表2中可以发现本文提出的混合模型同ANFIS模型和BPNN模型相比表现是最好的, 充分表明交通流周期性的提取, 进而利用残差数据训练模型这一方法对与提高交通流预测精度的重要性. 预测准确率提升情况如表3所示.
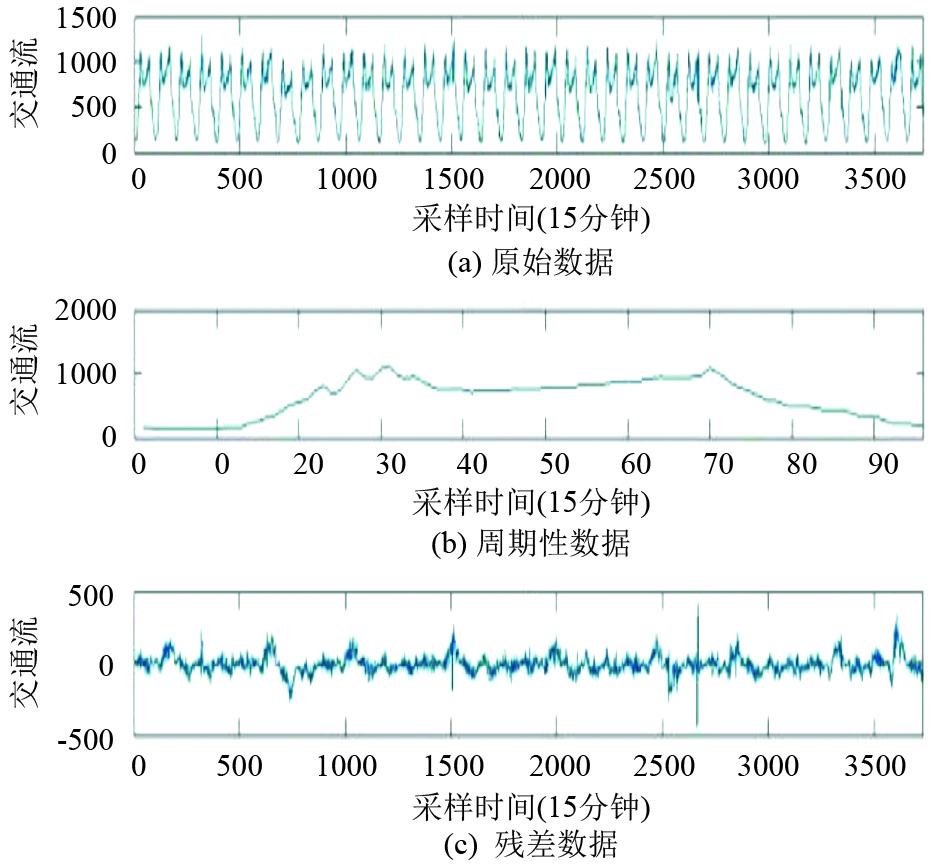
|
图 7 交通流数据(15分钟间隔) |

|
图 8 交通流预测结果(15分钟间隔) |
| 表 2 不同模型的指标对比(15分钟间隔) |
2) 图9为交通流数据和二次交通流预测实验的预测值之间的散点图. 图中可以看出交通流混合模型的预测值和实际交通流数据有着很小的差别, 反映了混合模型突出的预测准确度.
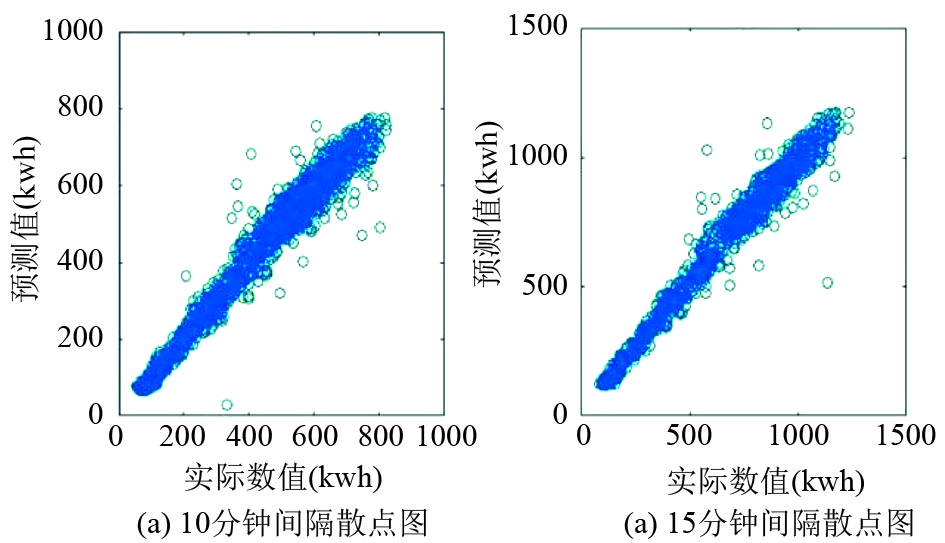
|
图 9 交通流散点图 |
| 表 3 交通流预测精度升降表(%) |
4 结语
本文提出了一个基于ANFIS的混合交通流预测模型, 提升了交通流预测的准确度, 该模型提取了交通流的周期性, 利用去除周期性数据的残差数据训练ANFIS模型, 进而得到交通流预测值. 本模型的理论贡献是将ANFIS模型和交通流周期性提取方法有机结合, 根据交通流周期性这一固有特征和ANFIS模型对交通流数据非线性特点的匹配, 组成ANFIS交通流预测混合模型. 另一方面, 该方法在交通流预测应用中的突出表现也在实验结果中得以验证, 证明了该混合模型的有效性和优先性.
众所周知, 很多数据如电力负荷、建筑能耗都有周期性特征的存在, 混合模型的方法同样适合应用于这些有相似时间序列的预测方向上. 随着大数据时代的不断发展, 其他同样具有周期性特征的预测应用如大数据环境下的建筑能耗预测是本文下一步的研究方向.
| [1] |
Zheng Y, Capra L, Wolfson O, et al. Urban computing: concepts, methodologies, and applications. ACM Transactions on Intelligent Systems and Technology (TIST), 2014, 5(3): 38. |
| [2] |
Zheng Y, Liu YC, Yuan J, et al. Urban computing with taxicabs. Proceedings of the 13th International Conference on Ubiquitous Computing. New York, NY, USA. 2011. 89–98.
|
| [3] |
Li YX, Zheng Y, Zhang HC, et al. Traffic prediction in a bike-sharing system. Proceedings of the 23rd Sigspatial International Conference on Advances in Geographic Information Systems. New York, NY, USA. 2015. 33:1–33:10.
|
| [4] |
Sun H, Liu HX. Short-term traffic forecasting using the local linear regression model. Center for Traffic Simulation Studies, 2002.
|
| [5] |
Dang XC, Yan L. Traffic flow prediction based on multivariate linear AR model. Computer Engineering, 2012, 38(1): 84-86. |
| [6] |
Williams BM, Hoel LA. Modeling and forecasting vehicular traffic flow as a seasonal stochastic time series process. 1999.
|
| [7] |
Williams BM, Hoel LA. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. Journal of Transportation Engineering, 2003, 129(6): 664-671. DOI:10.1061/(ASCE)0733-947X(2003)129:6(664) |
| [8] |
Tan MC, LI YJ, Xu JM. A hybrid ARIMA and SVM model for traffic flow prediction based on wavelet denoising. Journal of Highway and Transportation Research and Development, 2009, 26(7): 127-132, 138. |
| [9] |
朱征宇, 刘琳, 崔明. 一种结合SVM与卡尔曼滤波的短时交通流预测模型. 计算机科学, 2013, 40(10): 248-251, 278. DOI:10.3969/j.issn.1002-137X.2013.10.052 |
| [10] |
Fu H, Xu LH. SVR prediction method of short-term traffic flow for dynamic navigation system. Microcomputer Information, 2009, 25(8-3): 208-210. |
| [11] |
Hong WC, Dong YC, Zheng FF, et al. Forecasting urban traffic flow by SVR with continuous ACO. Applied Mathematical Modelling, 2011, 35(3): 1282-1291. DOI:10.1016/j.apm.2010.09.005 |
| [12] |
Oh SD, Kim YJ, Hong JS. Urban traffic flow prediction system using a multifactor pattern recognition model. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2744-2755. DOI:10.1109/TITS.2015.2419614 |
| [13] |
Huang WH, Song GJ, Hong HK, et al. Deep architecture for traffic flow prediction: deep belief networks with multitask learning. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2191-2201. DOI:10.1109/TITS.2014.2311123 |
| [14] |
罗文慧, 董宝田, 王泽胜. 基于CNN-SVR混合深度学习模型的短时交通流预测. 交通运输系统工程与信息, 2017, 17(5): 68-74. |
| [15] |
Yin HB, Wong SC, Xu JM, et al. Urban traffic flow prediction using a fuzzy-neural approach. Transportation Research Part C Emerging Technologies, 2002, 10(2): 85-98. DOI:10.1016/S0968-090X(01)00004-3 |
| [16] |
Quek C, Pasquier M, Lim BBS. POP-TRAFFIC: a novel fuzzy neural approach to road traffic analysis and prediction. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(2): 133-146. DOI:10.1109/TITS.2006.874712 |
| [17] |
Chan KY, Dillon TS. On-road sensor configuration design for traffic flow prediction using fuzzy neural networks and taguchi method. IEEE Transactions on Instrumentation & Measurement, 2012, 62(1): 50-59. |
| [18] |
Jang JSR. ANFIS: adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 1993, 23(3): 665-685. DOI:10.1109/21.256541 |
 2019, Vol. 28
2019, Vol. 28


