2. 江苏科技大学 电气与信息工程学院, 张家港 215600;
3. 南京邮电大学 管理学院, 南京 210023
2. School of Electrical and Information Engineering, Jiangsu University of Science and Technology, Zhangjiagang 215600, China;
3. School of Management, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
随着经济改革开放初期[1], 股份制开始诞生, 我国股票发行市场随即开始萌芽. 相比于美国市场, 我国股票市场的起步较晚, 但是经过三十多年经济的建设、证券制度和法规的逐步完善, 市场已经越来越趋于成熟规范化发展. 因此越来越多的人摇身变成"股民", 投身于浩瀚的“股市”之中.
随着中国股票市场的不断发展, 上市公司数量也在逐步递增, 流通于证券市场的股票数量也随之增加[2]. 每只股票都拥有几十个不同的层面、维度上的数据, 中小股民在面对多维度, 数量巨大的数据时就加大了基于股票技术层面上分析的难度. 投资者在处理过多的变量时, 容易造成分析过程的混乱.
为了实现较为准确的股票预测, 本文研究了MLP和BP神经网络模型, 并结合两种模型构造了MLBP模型, 分别将爬取的股票历史数据作为神经网络的输入集, 通过模型的调参处理, 得出预测的结果. 根据MSE误差对比分析选取误差最小的作为股票预测的应用模型, 并利用其找出每股变化所表现出来的动态运行规律, 为股市中广大中小投资者等弱势群体服务, 并指导其进行有效的价值投资[3].
1 模型建立 1.1 MLP模型MLP (Multi-Layer Perception)神经网络是一种结构为层层递进的人工神经网络, 一组输入变量可以被映射、传递到一组输出变量. 该网络输入层、隐藏层和输出层. 除了输入节点之外, 每个节点自身都带有一个非线性激活函数的神经元[4]. 隐藏层主要实现对输入空间的非线性映射, 输出层则是实现结果的线性分类.
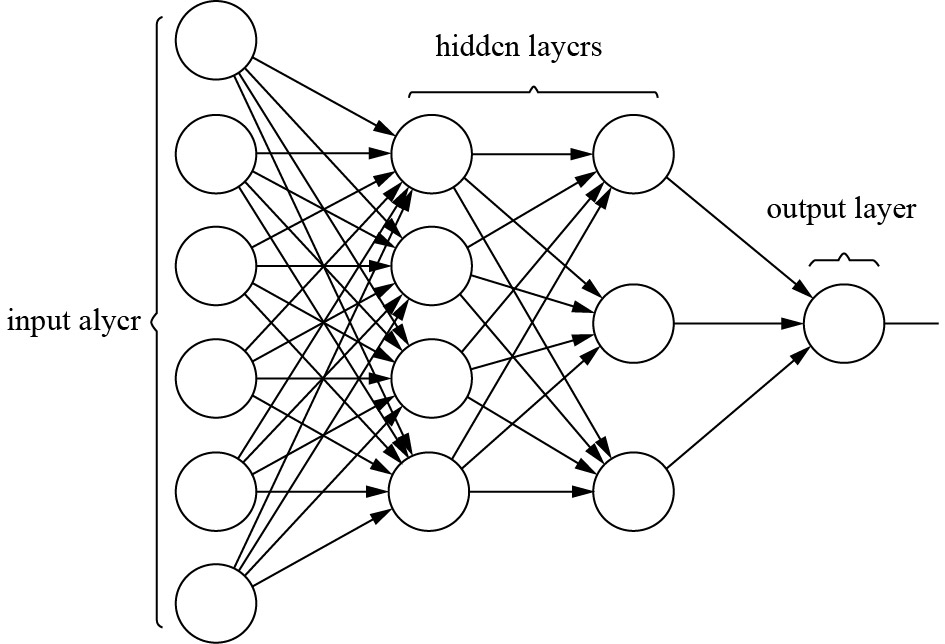
MLP网络有输入层(最左边), 隐藏层(中间两层), 和输出层(最右边), MLP只有向前传播过程. 每个神经元上面都有对于一个输入的权值、一个偏置和一个激活函数. 所以一个前向过程的流程就是input输入, 然后经过第一层神经元运算得到输出, 然后第一层的输出作为第二层的输入运算, 得到第二层的输出, 直到输出层运算, 最后得到结果. 神经网络就是依靠这样一套机制来进行计算和预测的. 神经网络模型图如图1.
|
图 1 MLP神经网络模型 |
1.2 BP模型
BP(Back Propagation)前馈神经网络, 是一种在MLP神经网络基础上改进的反馈型学习网络. 由两个阶段组成, 第一阶段是将训练输入送入网络以获得激励响应; 再将激励响应同训练输入对应的目标输出求差, 获得最后两层的响应误差; 第二阶段将输入激励和响应误差相乘获得权重的梯度; 再将这个梯度乘上一个比例并取反后加到权重上. 当整个训练网络输出层的误差缩小到期望值范围或训练次数超过阈值的时候, 所有训练过程才最终结束,这就是BP神经网络一次学习训练的全部过程.
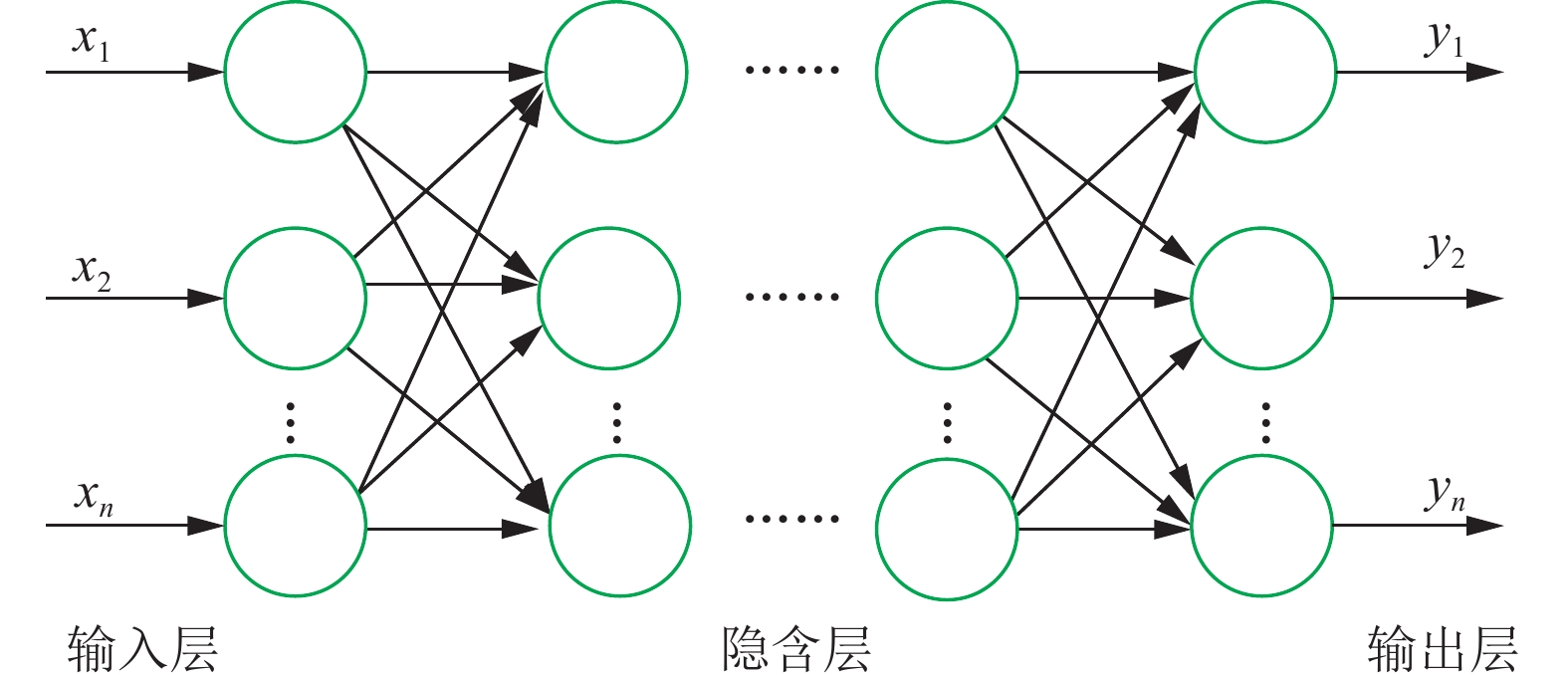
BP神经网络算法一般由三层或多层组成, 是一种多层前馈神经网络. 由输入层、输出层和隐含层组成[5]. 由于BP模型具有误差反向传播, 能够很好的改变网络的权值和阈值, 因此其具有泛化能力. 80%的人工神经网络中包含了BP网络[6,7], 所以是使用最广泛的神经网络模型[8], 在股票预测分析系统中也会将BP模型作为第一选择, BP算法的模型如图2所示.
|
图 2 BP神经网络模型图 |
假设输入节点
(1) 隐含节点输出公式:
| ${y_i} = f\left(\sum\limits_j {{W_{ij}}} - {\theta _i}\right) = f(ne{t_i})$ | (1) |
其中,
(2) 输出节点输出公式:
| ${O_{\rm{l}}} = f\left(\sum\limits_j {{T_{li}}} {y_i} - {\theta _{\rm{l}}}\right) = f(ne{t_i})$ | (2) |
其中,
(3) 输出节点误差的公式:
| $ \begin{split} E &= \dfrac{1}{2}\displaystyle\sum\limits_{\rm{l}} {{{({t_l} - {O_l})}^2}} = \dfrac{1}{2}\displaystyle\sum\limits_{\rm{l}} {{{\left({t_l} - f\left(\sum\limits_j {{T_{li}}} {y_i} - {\theta _{\rm{l}}}\right)\right)}^2}} \\ & = \dfrac{1}{2}\displaystyle\sum\limits_{\rm{l}} {{{\left\{ {t_l} - f\left[\sum\limits_j {{T_{li}}} f\left(\sum\limits_j {{W_{ij}}} - {\theta _i}\right) - {\theta _{\rm{l}}}\right]\right\} }^2}} \end{split} $ | (3) |
BP和MLP组合模型即为MLBP模型, 其是在BP模型和MLP模型的基础上进行改进的模型, 将MLP的多个隐含层放入到BP模型中, 因此MLBP模型是有1个输入层, 2个隐含层和1个输出层的反向传播神经网络.
MLBP模型的执行流程如下:
(1) 首先获取股票的历史数据及待预测的数据, 作为模型的输入集.
(2) 对数据进行预处理, 包括转置和归一化.
(3) 构建MLBP模型, 并初始化参数.
(4) 不断地进行调参进行训练, 直到训练次数达到一定数值, 保存训练数据训练出的模型(包括网络的层数、权值等参数).
(5) 带入待测数据, 进行预测, 并进行误差分析.
主要MLBP模型的流程图如图3所示.

|
图 3 MLBP模型流程 |
2 MSE误差分析
MSE (Mean Square Error)均方误差[9]是衡量训练模型的输出值与真实值之间平方误差的总体期望偏差, 如式(4)所示.
| $MSE(\hat \theta ) = E{(\hat \theta - \theta )^2}$ | (4) |
其中,
这里需要引入两个定义:
(1) 估计的偏差bias
| $bias{\rm{(}}\hat \theta {\rm{) = }}E{\rm{(}}\hat \theta {\rm{) - }}\theta $ | (5) |
其中, 期望作用在所有从随机变量采样得到的数据上,
(2) 方差Var
| $Var(\hat \theta ) = \frac{1}{m}\sum\limits_{i = 1}^m {{{({x^{(i)}} - \hat \mu )}^2}} $ | (6) |
其中,
此处, 可以根据式(5)、式(6)将式(4)改写为:
| $MSE = Bias{(\hat \theta )^2} + Var(\hat \theta )$ | (7) |
MSE包含了偏差和方差, 理想的估计具有较小的MSE或是在检查中会稍微约束它们的偏差和方差.
3 实验 3.1 实验过程与数据实验包括数据爬取和模型对比两部分. 首先通过Python提供的Tushare接口[10]爬取50天的股票数据信息, 对这些数据进行转置和归一化处理, 并将数据分成训练数据集和测试数据集存入数据库. 随后分别使用MLP、BP和MLBP模型对数据库中的股票数据进行训练和预测, 并根据实验数据进行模型对比.
实验中的调参包括: Sigmoid选取正切函数, 初始权重的范围在[−0.1,0.1]之间, 使用MSE计算误差. 设训练次数记为T,T取值300和500, 学习速率记为N, N取值0.05、0.1和0.15, 动量因子记为M, M取值0.1, 输入层记为I, 隐含层记为H, 输出层记为O, 误差记为E.
实验内容是根据50天的历史数据来预测未来3天的股票信息. 表1至表3分别是MLP、BP和MLBP的预测数据.
3.2 实验结果分析在这3种算法中, BP和MLBP模型计算的误差要远远小于MLP算法, 而MLBP模型相比BP模型误差进一步降低. 因为MLBP在训练参数和权值时用了反向传播并更新的过程, 所以能够更加准确的进行预测. 模型误差对比如图4所示.
| 表 1 50天数据预测3天数据表(MLP模型) |
| 表 2 50天数据预测3天数据表(BP模型) |
| 表 3 50天数据预测3天数据表(MLBP模型) |
三种模型的误差都非常均匀, 因此预测的结果具有平稳性. 但是三种算法的都有的缺点是当选取的数据量特别多时, 会导致训练时间过长, 而较少的数据量虽然能够加快运算速度, 但预测的误差会变大, 因此选择合适的数据规模可以权衡误差与效率.

|
图 4 模型误差对比图 |
4 MLBP模型的应用 4.1 股票分析平台
通过对股票数据的训练和预测实验, 可证明MLBP模型更能够准确的对股票数据进行分析, 因此其在股票分析方面具有潜在的应用价值[11].
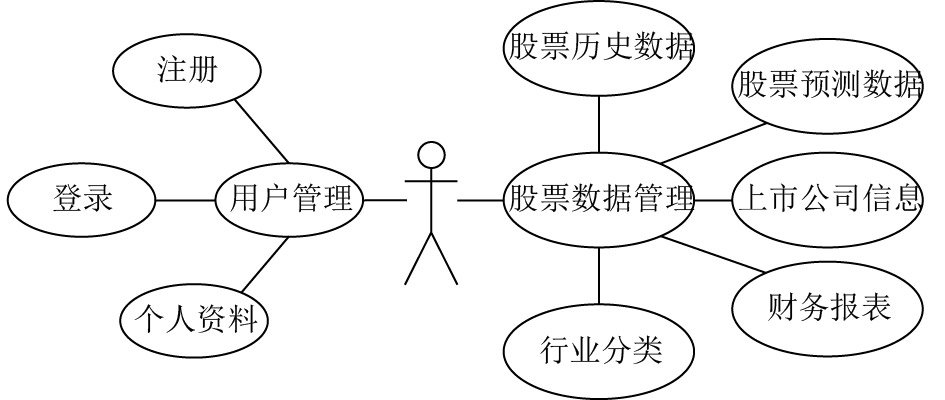
为了能够极大地发挥该模型的作用, 同时让用户更加方便的进行股票数据的分析和预测, 本文将该模型应用于股票分析平台. 该平台为Django框架[12]的WEB应用程序, 以MLBP模型作为平台的核心业务部分. 另外增加了注册登录、上市公司信息、财务报表、行业分类等功能作为辅助部分. 平台的用例图和功能模块图分别如图5、图6所示.
|
图 5 平台用例图 |
4.2 平台功能设计
平台包括用户、股票、企业、企业报表等实体, 各个实体之间具有一定关联性包括:
(1) 每个用户可以查看所有股票基本信息、查看所有企业信息和所有企业报表信息.
(2) 每只股票对应一个企业, 并且每只股票的所有信息能被所有用户查询.
(3) 每份企业报表都可以被所有用户查看, 每份企业报表对应一个企业.
(4) 每个企业对应一只股票, 并且拥有许多企业报表, 每个企业可以被所有用户查看.
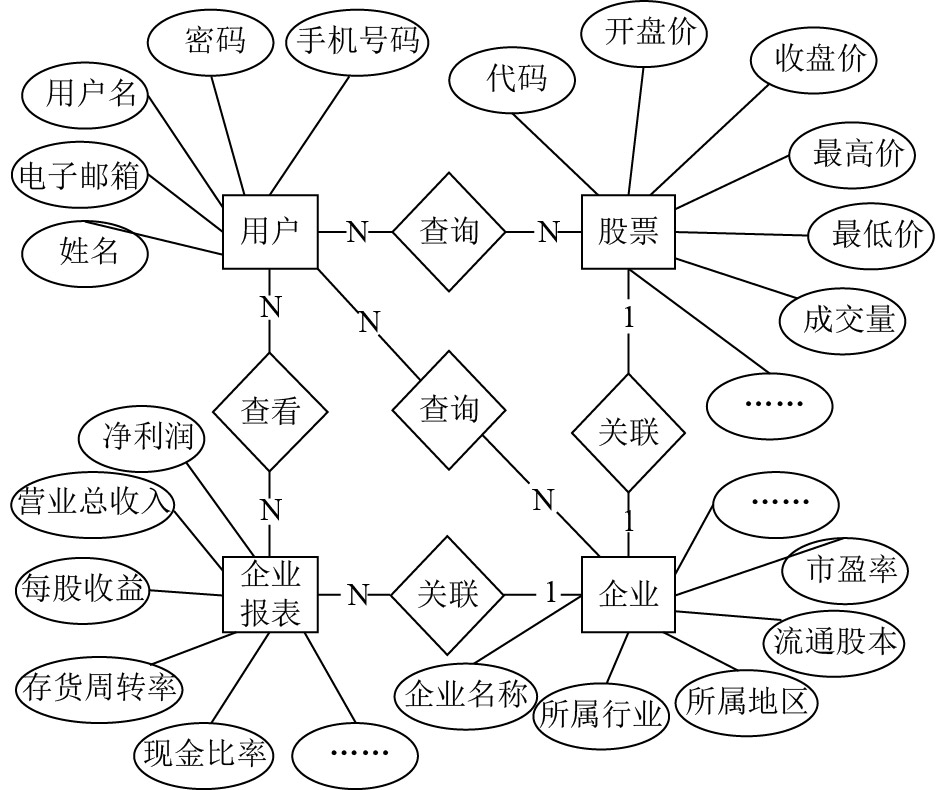
实体关系(E-R)图如图7所示.
|
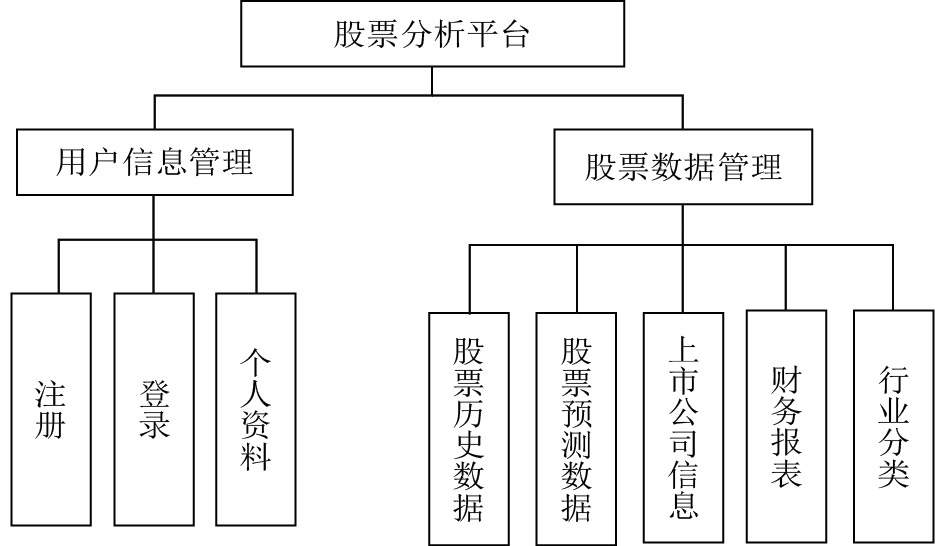
图 6 平台功能模块图 |
|
图 7 平台E-R图 |
4.3 平台运行
平台部署在本地服务器上, 通过访问项目网址可展示平台界面. 平台首页如图8所示.
以股票行情预测模块为例, 用户在头部输入框中输入查询的股票代码, 系统后台调用财经数据接口获取交易数据, 并将数据放入神经网络算法代码中处理, 将各个算法的输出值使用MSE误差估计模型进行比较, 最后得出最佳的预测结果. 后台将运行结果返回到前台页面展示, 如图9所示.

|
图 8 平台首页 |
|
图 9 股票行情预测界面 |
5 结语
通过分析现今的股票市场发展, 根据众多中小投资者对股市信息的预测需求, 本文研究了MLP、BP和MLBP模型, 并通过实验和模型对比可知, MLP和BP组合模型可以进一步提高预测的准确度, 降低误差率, 从而使投资者可以根据预测的股票信息更清楚的进行投资决策. 另外通过将MLBP应用在WEB程序中, 更加方便了用户操作, 提高了模型的应用价值.
在接下来的工作中, 还会继续完善MLBP模型, 在降低误差的基础上进一步提高运行速率. 同时广泛爬取不同种类的股票信息, 拓展股票分析平台的功能, 为不同需求的用户提供多方面服务.
| [1] |
牛新建. 中原证券股票分析预测系统设计与实现[硕士学位论文]. 大连: 大连理工大学, 2009. 5–6
|
| [2] |
孙睿. 区间型符号数据分析在股票分析中的应用[硕士学位论文]. 北京: 首都经济贸易大学2010. 23–24.
|
| [3] |
艾小刚. 价值投资理论在A股估值中的有效性研究[硕士学位论文]. 兰州: 兰州大学, 2014.
|
| [4] |
姚运涛. 面向股票的网络舆情信息处理与波动趋势预测[硕士学位论文]. 北京: 北京邮电大学, 2017.
|
| [5] |
Zhang YD, Wu LN. Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network. Expert Systems with Applications, 2009, 36(5): 8849-8854. DOI:10.1016/j.eswa.2008.11.028 |
| [6] |
Yin Z, Zhou ZR. A study of wind statistics through auto-regressive and moving-average (ARMA) modeling. China Ocean Engineering, 2001, 15(1): 61-72. |
| [7] |
Eric D, Andjelic GB, Redzepagic S. Application of MACD and RVI indicators as functions of investment strategy optimization on the financial market. Zbornik Radova Ekonomskog Fakultetau Rijeci, Časopisza Ekonomsku Teorijui Praksu, 2012, 27(1): 171-196. |
| [8] |
陈伟, 吴耀武, 娄素华, 等. 基于累积式自回归动平均法和反向传播神经网络的短期负荷预测模型. 电网技术, 2007, 31(3): 73-76. DOI:10.3321/j.issn:1000-3673.2007.03.015 |
| [9] |
杨迪, 邵玉斌, 陈家福. 基于MSE准则的线性均衡器性能分析. 昆明理工大学学报(理工版), 2006, 31(6): 42-45. DOI:10.3969/j.issn.1007-855X.2006.06.010 |
| [10] |
邵必林, 梁元欣. 基于MLP与RBF神经网络的钼金属价格预测方法研究. 中国钼业, 2016, 40(5): 54-60. |
| [11] |
桂新志. 数据挖掘在股票分析中的研究与应用[硕士学位论文]. 武汉: 华中科技大学, 2011.
|
| [12] |
夏志富, 王晗璐, 李玉平, 等. 基于Django框架的智能商务监控系统的设计. 微型机与应用, 2016, 35(12): 21-23, 27. |
 2019, Vol. 28
2019, Vol. 28


