2. 中国科学院 沈阳计算技术研究所, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China
我国是一个农业大国, 农业在国民经济中占据着重要地位, 农业是否平稳健康发展, 关系着社会的稳定. 所以, 对农产品物价进行预测具有迫切的现实意义.
之前人们大多采用单一模型进行预测, 近年来人们更多的是采用组合模型进行预测. 陈咏梅[1]等使用基于ARIMA和BP神经网络[2]的组合模型对福建滨海旅游市场规模进行预测, 表明该组合模型的预测准确率高, 更加接近真实情况. 朱叶[3]等使用灰色模型和BP神经网络构建的组合模型对兵团农产品物流市场需求进行预测, 表明组合模型在预测精度上有了很大的提升. 刘金源[4]等使用基于BP神经网络、GM灰色预测理论和PCA主成分分析的组合模型对城市燃气日负荷进行预测, 表明该组合模型[5,6]是一种更为有效的预测方法. 组合模型展现出了更大的优势. 本文使用粒子群和动态学习率优化BP神经网络模型, 结合支持向量机模型对农产品物价进行预测, 将两组预测结果使用优化的BP神经网络进行组合得到预测结果, 提高模型的泛化能力和预测准确度.
2 BP-SVR-BP组合模型 2.1 组合模型组合方式组合模型是利用两种或者两种以上的模型, 分别对实际问题进行模型训练, 将结果使用权重进行组合, 得到最终结果的过程. 组合模型目标就是利用一组最优权重系数, 对单独模型结果进行加权求值, 使得结果更加接近真实值.
目前, 单一预测模型准确率不高, 考虑因素单一, 没有结合模型的适用场景, 所以本文研究了组合模型. 由于BP神经网络能够更好地模拟线性和非线性数据, 适合于长期预测模型的训练; SVR是基于时间序列的回归预测模型, 适合于短期预测. 将适合中长期预测的BP模型和适合于短期预测的SVR模型组合, 使模型具有更高的准确率, 更强的泛化能力. 所以选用了优化后的BP神经网络模型和SVR模型进行组合. 提出了基于BP-SVR-BP的组合模型算法, 即BP神经网络-支持向量机回归-BP神经网络的组合模型, 并且使用农产品价格数据对模型进行验证评估.

|
图 1 BP-SVR-BP组合模型 |
图1为BP-SVR-BP组合模型的结构图. 第一步将经过数据预处理的训练集数据(train_data)输入到SVR算法中, 经过训练, 得到SVR模型(M1); 同时将训练集数据输入第一轮的BP神经网络算法中, 经过训练, 得到BP神经网络模型(M2). 第二步将实验数据或者称之为测试数据(test_data)输入到SVR和BP模型中, 得到两组实验结果数据(P1, P2), 将其组成两列数据, 并且将其对应的真实数据(Price)加入, 作为第三列, 形如(P1, P2, Price)组成第二轮BP神经网络算法的训练集数据(new_data). 第三步将新的训练集数据(new_data)输入BP神经网络算法, 这一步主要是利用BP拟合组合模型的权重系数, 寻找最优的权重系数组合. 经过训练, 得到第二轮的BP模型(M3). 第四步将实验数据(test_data1)输入模型(M3), 得到预测结果, 评价组合模型的预测准确度.
在组合模型中, 第一轮我使用了优化的BP神经网络模型和基于多项式核函数的SVR模型, 第二轮使用了优化的BP神经网络模型训练组合模型权重系数.
2.2 优化BP神经网络本文采用三层结构, 即输入层、隐含层、输出层. 假设输入层n个节点, 隐含层k个节点, 输出层1个节点. X(X1, X2, …, Xn)为输入层输入数据; M(M1, M2, …, Mn)为经输入层加权求和的结果, 即隐含层的输入数据; N(N1, N2, …, Nk)为隐含层由激活函数求得的结果, 即隐含层的输出数据; Z为经隐含层加权求和的结果, 即输出层的输入数据; Y为预测值, W为各层链接的权值, B(B1, B2, …, Bi)表示偏置值.
根据输入X, 得隐含层的输入为:
| ${{M}}_j^{} = \sum\limits_{i = 1}^n {W_{ij}^{(l)}} {X_i} + B_i^{(l)}$ | (1) |
其中,
| ${{{N}}_j} = {\psi _1}({M_j}) = {\psi _1}\left(\sum\limits_{{{i}} = 1}^n {W_{ij}^{(l)}{X_i} + B_i^{(l)}}\right) $ | (2) |
其中,
输出层的输入为:
| ${{Z}} = \sum\limits_{j = 1}^k {W_{j1}^{(l)}{N_j}} + B_j^{(l)}$ | (3) |
输出层的输出为:
| ${{{Y}}_{}} = {\psi _2}\left( Z \right) = {\psi _2}\left( {\sum\limits_{j = 1}^k {W_{j1}^{(l)}{N_j} + B_j^{(l)}} } \right)$ | (4) |
由于BP神经网络的权值和阈值对价格的预测准确度有一定影响, 可以通过粒子群算法对网络中的权值和阈值进行全局寻优, 合理优化调整. 假设给定n个粒子:
| $v_{iD}^{k + 1} = \omega v_{iD}^k + {c_1}{r_1}\left( {p_{iD}^k - x_{iD}^k} \right) + {c_2}{r_2}\left( {p_{gD}^k - x_{iD}^k} \right)$ | (5) |
位置更新为:
| $ x_{iD}^{k + 1} = x_{iD}^k + v_{iD}^{k + 1} $ | (6) |
假设输入层、隐含层、输出层节点数为L1_Num, L2_Num, L3_Num. 种群参数初始化为: 种群数目N; 维度为D=L1_Num×L2_Num+L2_Num×L3_Num; 使用真实值与预测值的均方误差作为粒子群适应度函数:
| $ e = \frac{1}{n}\sum\limits_{j = 1}^n {{{\left( {{O_j} - {Y_j}} \right)}^2}} $ | (7) |
其中,
BP神经网络的学习率对网络的收敛速度有影响整.
| $ \eta (k) = \left\{ {\begin{array}{*{20}{c}} 1.05\eta (k - 1),& E(k + 1) < E(k)\\ 0.75\eta (k - 1), &E(k + 1) > E(k)\\ \eta (k), &E(k + 1) = E(k) \end{array}} \right. $ | (8) |
支持向量回归机(SVR)模型是在SVM基础上, 加以改进, 可以用于基于回归的预测模型. 模型主要是通过核函数将数据映射到一个高维空间, 然后在高维空间寻找一个最优的超平面, 使所有点到该平面的距离误差最小. 这个函数即是SVR函数模型. SVR函数为:
| $f(X) = {W^{\rm{T}}}\phi (X) + b$ | (9) |
其中,
| $ \mathop {\min }\limits_{w, {\xi _i}, {{\hat \xi }_i}} \left( {\frac{1}{2}{{\left\| w \right\|}^2} + C\sum\limits_{i = 1}^m {\left( {{\xi _i} + {{\hat \xi }_i}} \right)} } \right) $ | (10) |
同时必须满足:
| $ \left\{ \begin{array}{l} f({x_i}) - {y_i} + b \le \varepsilon + {\xi _i}\\ {y_i} - f({x_i}) - b \le \varepsilon + {{\hat \xi }_i}\\ {\xi _i} \ge 0, {{\hat \xi }_i} \ge 0, i = 1, 2, \cdots, m \end{array} \right. $ | (11) |
数据选用2009-2016年上海农产品日价格数据作为实验数据.
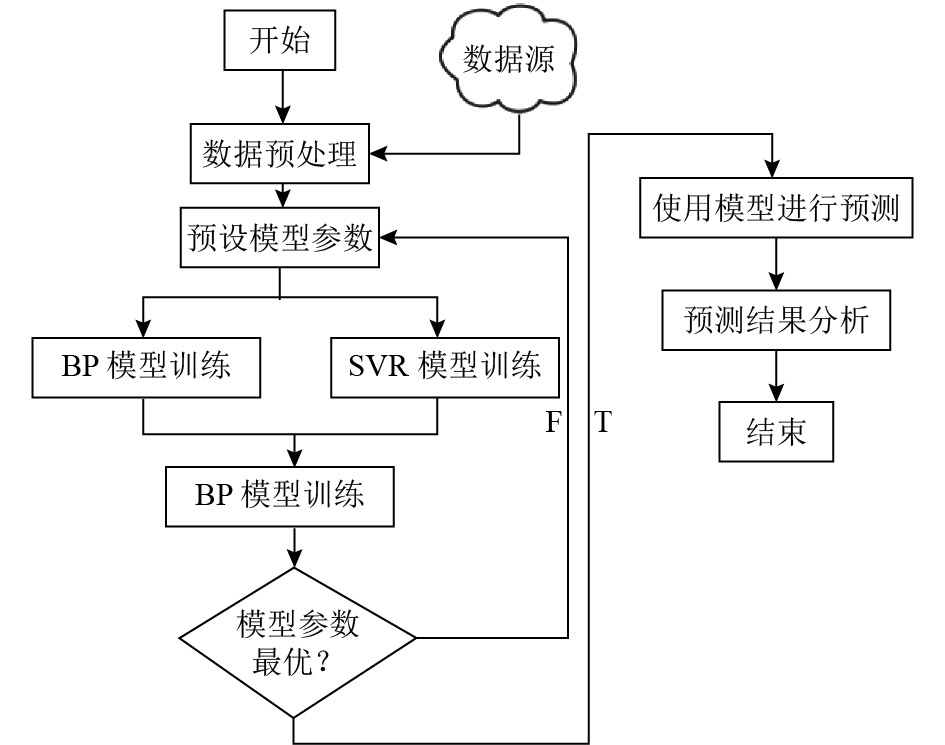
|
图 2 构建模型流程图 |
3.2 数据预处理
选用数据的平均交易价格作为预测目标, 数据发布时间、最低交易价格、最高交易价格、最高温度、最低温度作为模型输入数据, 训练模型.
(1) 将数据发布时间转换为YYMMDD的时间格式, 例如2016/6/11转换为20160611.
(2) 采用前后k个数据的平均值填充缺失值.
(3) 采用MIN-MAX方法对特征数据归一化.
3.3 组合模型训练(1) 预处理之后的数据, 选用集合数据(train_data)的70%作为训练数据(Train1), train_data的30%的数据作为测试数据(Test1). 将Train1数据分别输入到SVR算法和BP算法中训练出SVR模型(M1)和BP模型(M2). 将Test1输入到M1和M2模型中, 得到两组预测结果(P1, P2), 和真实数据(Price)组成三列数据(train_data2), 形如(P1, P2, Price). 将train_data2的80%作为训练集(Train2), train_data2的20%作为测试集(Test2), Train2训练集训练BP模型, 得到最优权重系数组合, 得到模型M3. 将Test2输入M3模型得到预测结果值.
(2) 对BP神经网络训练, 选择最优隐含层节点数目. 使用均方根误差(RMSE)衡量真实值和预测值之间的准确率, 如图3.
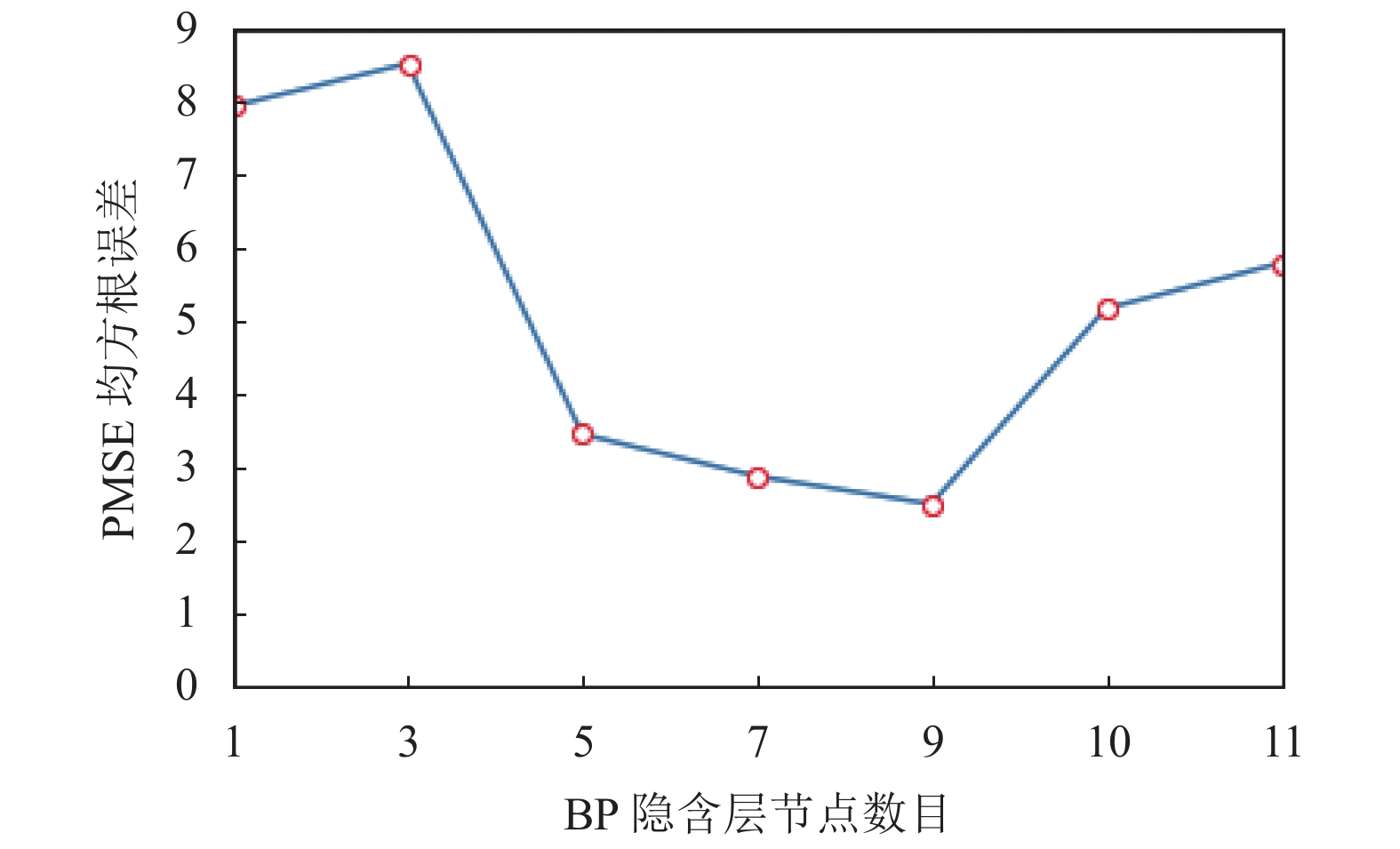
|
图 3 隐藏层节点数-RMSE图 |
根据图3, BP隐含层节点数目为9.
(3) SVR模型, 选用多项式核函数(Poly).
4 实验结果与分析 4.1 与单一模型对比分析本文基于BP-SVR-BP组合模型, 第一个BP网络模型使用了5个节点的输入层, 9个节点的隐藏层, 1个节点的输出层, 网络权值和阈值使用粒子群算法进行全局优化, 加以自适应动态调整学习率; SVR选用多项式核函数进行训练; 第二个BP神经网络使用2个节点的输入层, 5个节点的隐含层, 1个节点的输出层. 预测结果如图4.
图4描绘了时间与价格预测值的折线图, 从图中可以得出BP神经网络, SVR模型, BP-SVR-BP模型, 总体趋势相近, 但BP, SVR局部存在较大差距, BP-SVR-BP组合模型局部更符合价格数据趋势. 将折线图放大, 如图5所示.

|
图 4 时间-价格图 |

|
图 5 时间-价格图 |
从图5中, 可以得出, SVR模型预测的值离真实值曲线最远, BP神经网络次之, BP-SVR-BP模型最近, 说明BP-SVR-BP模型的预测准确度最高, 所以BP-SVR-BP预测准确率上优于单一的BP, SVR模型.
为了更加准确地评价三个预测模型, 采用量化体系进行评价. 采用MAE, MSE, RMSE进行量化评价.
测得的结果见表1.
| 表 1 单一模型对比 |
从表1中, 可以从量化的角度分析得出, BP-SVR-BP模型, MAE, MSE, RMSE的值都比BP和SVR模型小, 基于以上综合分析, 得出BP-SVR-BP组合预测模型对农产品价格曲线拟合效果更优, 预测准确率更高.
4.2 与组合模型对比分析前人的研究中, 也尝试了很多的组合模型预测算法. 比如使用BP神经网络模型和ARIMA模型进行组合, 首先通过ARIMA模型预测结果值, 接着使用预测值作为参数, 输入BP神经网络预测, 得出预测结果, 即为BP-ARIMA模型. 也有采用BP神经网络模型和灰色模型GM(1, 1)进行组合, 将结果采用标准差确定组合模型组合权重, 将单一模型结果组合, 得出预测结果, 即为BP-GM(1, 1)组合模型. 现将提到的预测方法用在农产品价格预测上, 对组合模型进行对比分析,如图6.

|
图 6 组合模型时间-价格图 |
图6分别描绘了BP-SVR-BP、BP-ARIMA、BP-GM(1, 1)组合模型在农产品价格中的预测结果, 从图中可以清晰地看出, 三种组合模型对农产品价格曲线模拟较好, 都能够比较准确地模拟出农产品价格走势, 和真实农产品价格走势相同, 但是从图6中也可以得出, 三种模型虽然走势相同, 但是准确率上却有差别, BP-SVR-BP模型描绘的曲线相对于BP-ARIMA、BP-GM(1, 1)模型描绘的曲线, 更加逼近真实数据曲线, 即为准确率更高. 采用量化体系分析结果如表2.
从表2中, 可以从量化的角度分析, BP-SVR-BP组合模型的MAE, MSE, RMSE值都比BP-ARIMA、BP-GM(1, 1)组合模型的小, 所以可以得出BP-SVR-BP组合模型的准确率更好, 泛化能力更强, 能够更好地实现农产品物价的预测.
| 表 2 组合模型对比分析 |
5 结语
本文提出了基于BP-SVR-BP的组合模型, 使用图分析和数据量化分析, 分析了BP模型、SVR模型、BP-SVR-BP组合模型, 得到组合模型准确率更高, 拟合效果更优. 紧接着对常见的组合模型进行了对比分析, 对BP-SVR-BP组合模型、BP-ARIMA组合模型、BP-GM(1, 1)组合模型三种组合模型进行了图分析和数据量化分析, 得出BP-SVR-BP组合模型相对于BP-ARIMA和BP-GM(1, 1)组合模型准确率更好, 泛化能力更强, 能够较好地实现农产品物价的预测. 本方法还有继续需要改进的地方, 比如说, 将对农产品价格产生影响的更多影响因素纳入模型训练中, 对SVR核函数进行优化, 对组合模型组合预测结果的加权值进行优化等等. 未来将继续对组合模型进行深入研究, 深化改进模型, 得到更优组合.
| [1] |
陈咏梅. 基于BP-ARIMA组合模型的福建滨海旅游市场规模预测. 厦门理工学院学报, 2018, 26(4): 22-26. |
| [2] |
马健, 盛魁, 董辉. 基于改进型误差函数的复值BP神经网络对股票价格的预测研究. 长春师范大学学报, 2018, 37(6): 85-90. |
| [3] |
朱叶, 喻晓玲. 基于组合模型的兵团农产品物流市场需求预测. 塔里木大学学报, 2016, 28(2): 52-60. DOI:10.3969/j.issn.1009-0568.2016.02.010 |
| [4] |
刘金源, 王寿喜, 李婵. 城市燃气日负荷PCA-GM-BPNN组合预测模型. 天然气与石油, 2018, 36(5): 13-19. DOI:10.3969/j.issn.1006-5539.2018.05.003 |
| [5] |
吴叶, 刘婷婷, 方少勇. 基于MIV-GA-BP神经网络的我国棉价预测研究. 棉纺织技术, 2018, 46(7): 77-80. DOI:10.3969/j.issn.1001-7415.2018.07.020 |
| [6] |
江粉桃. 非线性方法的时间序列组合模型在农产品价格预测中的应用研究[硕士学位论文]. 兰州: 兰州交通大学, 2018.
|
 2019, Vol. 28
2019, Vol. 28


