竞争算法优化BP神经网络性能研究

引用本文

卢滢宇. 竞争算法优化BP神经网络性能研究. 计算机系统应用, 2019, 28(5): 173-177.http://www.c-s-a.org.cn/1003-3254/6903.html

Lu YY. Performance Study of BP Neural Network Based on PK Algorithm. Computer Systems and Applications, 2019, 28(5): 173-177(in Chinese).http://www.c-s-a.org.cn/1003-3254/6903.html

竞争算法优化BP神经网络性能研究

卢滢宇

宁波职业技术学院公共教学部, 宁波 315800

收稿日期：2018-11-29; 修改日期：2018-12-12; 采用时间：2018-12-26; csa 在线出版时间：2019-04-28

基金项目：宁波职业技术学院2018年校级青年课题(NZ18027)

摘要：针对诸多群智能算法容易陷入局部最优、收敛速度慢的特点, 提出一种参数设置少, 全局搜索能力强的竞争算法. 通过10个基准函数与粒子群算法的比较, 30次试验下竞争算法的平均值与最小值均优于粒子群算法, 验证了该算法的有效性. 用竞争算法优化BP神经网络, 并对11个测试数据集进行分类, 实验结果表明, 用竞争算法优化后的BP神经网络在11个测试集上性能均优于原始算法, 且在大部分测试集上性能优于用遗传算法优化的BP神经网络. 该算法能有效提高分类正确率, 增强鲁棒性.

关键词: BP神经网络竞争算法基准函数测试数据集

Performance Study of BP Neural Network Based on PK Algorithm

LU Ying-Yu

Public Teaching Department, Ningbo Polytechnic, Ningbo 315800, China

Foundation item: Year 2018, Ningbo Polytechnic Fund for Young Talent (NZ18027)

Abstract: Aiming at the characteristics that many cluster intelligent algorithms are easy to fall into local optimum and have slow convergence rate, a new algorithm (PK algorithm) with less parameter settings and strong global search ability is proposed. The comparison of 10 benchmark functions with particle swarm optimization algorithm verifies the effectiveness of the algorithm, because the average and minimum values of the PK algorithm under 30 trials are better than the particle swarm optimization algorithm. Then using the PK algorithm to optimize the BP neural network, and 11 test data sets were classified. The experimental results show that the BP neural network based on PK algorithm has better performance than the original algorithm on 11 test sets, and the performance is superior to BP neural network based on genetic algorithm on most test sets. Thus, we conclude that the BP neural network based on PK algorithm can effectively improve the classification accuracy and enhance the robustness.

Key words: BP neural network PK algorithm benchmark functions test data set

BP神经网络是一种信号前向传递, 误差反向传播的多层前馈神经网络. 由于强大的泛化能力, BP神经网络被广泛应用于模式分类^[1–3]、故障诊断^[4,5]及非线性拟合预测^[6]等方面. 但BP神经网络尚有以下不足: (1)初始权重与阈值随机产生, 导致网络优化不稳定, 输出结果波动较大. (2)通过梯度下降法训练修正权值阈值^[7], 使得算法容易陷入局部最优, 全局搜索能力不强.

为了克服上述问题, 众多学者从各个角度对BP神经网络进行改进, 而将遗传算法、粒子群算法、蜂群算法等群智能算法用于优化BP神经网络成了研究的一大热点^[8–13]. 群智能算法往往原理简单, 参数设置少, 优化结果较好, 在资源分配、调度优化、工程应用等各领域都有应用^[14–16]. 但是群智能算法亦存在缺陷: 遗传算法全局搜索能力强, 但收敛速度慢; 粒子群算法参数个数少, 但后期种群多样性低, 容易陷入局部最优; 蜂群算法流程相对复杂, 局部开发能力较弱; 猴群算法搜索速度慢, 求解精度不高. 为了提高群智能算法的搜索与开发能力, 学者们从优化参数^[17]、反向搜索^[18]、构造混沌映射以开发搜索区域^[8]、邻域内增强局部搜索^[11]、引入诱导过程^[14]、复制新粒子进行不同程度变异^[19]等方式来提高寻优能力, 开发种群多样性, 这些方法提高了原算法的计算精度, 但是也使得算法流程变得复杂, 计算量增加.

目前大多学者利用群智能算法来优化BP神经网络的初始权值与阈值, 这亦存在如下问题: 通过群智能算法优化的初始权值阈值, 经再次训练后作分类预测, 由于训练过程中样本顺序的随机性, 导致训练的网络不稳定, 优化后预测精度提高不明显, 更好的方法是将整个优化后的训练网络保留下来, 一方面可以降低训练成本, 另一方面也能提高预测精度. 针对BP神经网络与群智能算法的以上问题, 本文首先提出了一种新的算法--竞争算法. 这种算法的优点在于参数设置少, 流程简易, 计算量小, 且具有远高于粒子群算法的全局搜索能力, 提高搜索精度. 然后将此算法用于优化BP神经网络, 可以有效提高BP神经网络优化性能, 增强网络的鲁棒性.

1 算法原理及改进 1.1 竞争(PK)算法

在众多群智能算法中, 遗传算法、粒子群算法以及蜂群算法是目前运用较多的几种算法. 其中粒子群算法因其流程简明、参数少而广泛受到学者的青睐. 但粒子群算法也同其他群智能算法一样, 容易陷入局部最优. 因此, 改进已有的算法或者寻找搜索能力更强的智能算法是众多学者研究的焦点. 受粒子群算法启发, 我们给出一种新的算法, 并为其命名为竞争(PK)算法, 该算法不仅流程简洁, 参数较粒子群算法更少, 且全局搜索能力强于粒子群算法. PK算法的优化流程如下:

(1)初始化. 设定种群规模为N, 首先随机生成初始种群即N个个体, 每个个体 ${x_i} = ({x_{i1}}, {x_{i2}}, \cdots, {x_{iD}})$ 是一个D维向量, 代表问题的一个解. 随机生成每个个体对应的初始速度 ${v_{id}} = ({v_{i1}}, {v_{i2}}, \cdots, {v_{id}})$ , 并限定个体与速度的上下界 $[{x_{\min }}, {x_{\max }}]$ 、 $[{v_{\min }}, {v_{\max }}]$ .

(2)个体评价. 根据问题计算每个个体的适应度函数 $f({x_i})$ 以评价个体优劣, 并记录最优个体.

(3)对每个个体 ${x_i}$ (称之为主动挑战者), 随机找另一个体 ${x_j}$ (称之为被动挑战者)来做PK. 如果 ${x_i}$ 更优, 则通过向 ${x_i}$ 学习修正 ${x_j}$ , 反之修正 ${x_i}$ . 个体第d维修正公式如下:

修正主动挑战者 ${x_i}$ :

${v_{id}}^{t + 1} = {w_1} \cdot {v_{id}}^t + rand \cdot ({x_{jd}}^t - {x_{id}}^t)$

(1)

${x_{jd}}^{t + 1} = {x_{jd}}^t + {v_{jd}}^{t + 1}$

(2)

修正被动挑战者 ${x_j}$ :

${v_{jd}}^{t + 1} = {w_2} \cdot {v_{jd}}^t + rand \cdot ({x_{id}}^t - {x_{jd}}^t)$

(3)

${x_{id}}^{t + 1} = {x_{id}}^t + {v_{id}}^{t + 1}$

(4)

其中, ${w_1}, {w_2}$ 分别为主动挑战者和被动挑战者的惯性权重. t表示个体迭代的代数. 确保个体与速度都在预定的上下界范围内.

(4)如果达到终止条件则停止, 否则返回(2).

从上述流程可以看出, 竞争算法只有 ${w_1}$ , ${w_2}$ 两个参数, 流程简单, 主要只有PK与修正两种运算, 所以迭代计算量小. 与粒子群算法相比, 粒子群算法主要是向全局最优及个体最优的方向学习, 所以容易陷入局部最优; 而竞争算法每次的学习对象都是随机产生的, 能更好地保持种群的多样性, 从而更容易跳出局部最优. 此外, 每次都是PK失败的个体得到修正, 这既保留了适应度好的个体, 也进化了适应度差的个体, 有效提高了算法的收敛速度.

1.2 PK-BP神经网络

BP神经网络一般有1个输入层、1个或多个隐含层, 以及1个输出层. 优化流程为: 给定初始权值与阈值, 在BP神经网络输入层输入向量, 输入向量经与权值、阈值及激活函数做一定运算后到达隐含层, 再经与权值、阈值及激活函数做一定运算后到达输出层, 如果输出层不能得到期望的输出, 则反向传递期望输出与实际输出的误差, 调整权值与阈值, 重复此流程, 不断减少误差. BP神经网络学习能力强, 能解决任意复杂的模式分类问题和多维函数映射问题.

BP神经网络自身存在一定的局限性, 如优化过程中容易陷入局部最优值, 且因为训练过程中训练样本的输入顺序是随机的, 同一初始权值阈值下优化出来的网络性能存在差异. 为了提升优化精度, 提高全局搜索能力, 增强BP神经网络的鲁棒性, 采用竞争算法来优化BP神经网络. 其基本流程如下:

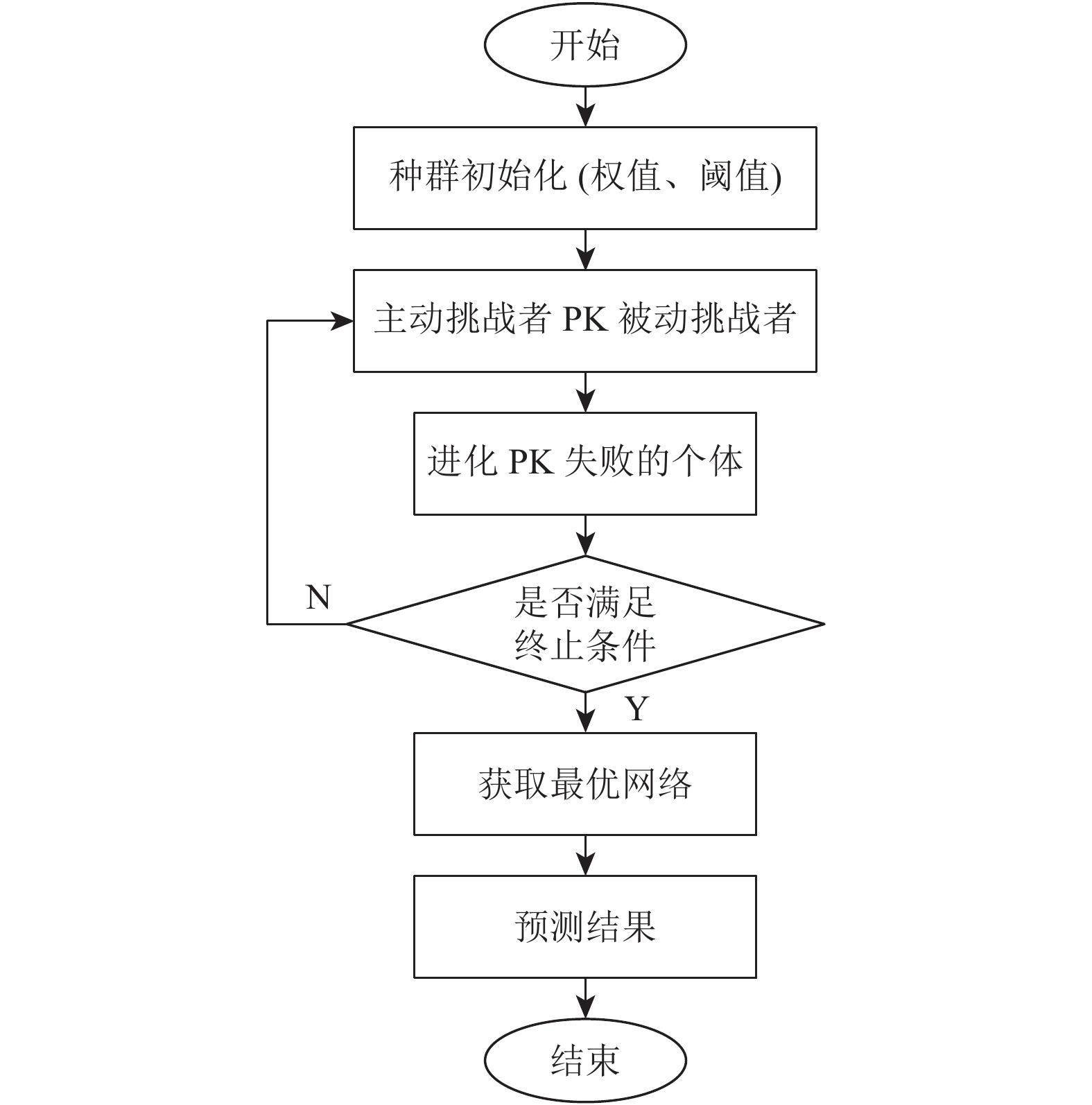
图 1 算法流程

具体实现步骤如下:

(1)设定竞争算法参数, 初始化种群, 其中每个个体均表示BP神经网络的初始权值和阈值, 个体维度的计算由式(5)计算:

$D = I \times H + H + H \times O + O$

(5)

其中, 神经网络的隐含层个数为1, $I$ 、 $H$ 、 $O$ 分别为输入层、隐含层、输出层的神经元个数.

(2)利用竞争算法优化神经网络内部权值、阈值. 其中适应度函数即为神经网络训练指定次数之后实际输出值与期望输出值的绝对误差之和, 在分类问题里取分错类的总个数.

(3)将最优网络保存下来使之形成“虚拟”函数, 来作为高精度的预测网络模型, 进一步用于分类预测, 并评价测试集的分类正确率.

由于竞争算法收敛速度快, 高维度下全局收敛能力强, 经竞争算法优化后的BP神经网络预测性能高. 不同于以往的利用群智能算法来优化初始权值与阈值, 而是利用优化好的网络直接加以预测, 不仅能减少重新训练网络所需的时间代价, 而且利用最好的网络状态进行分类预测, 可以有效避免因重新训练时样本顺序的随机性而导致的精度稳定性不高问题.

2 算法结果与分析 2.1 竞争(PK)算法性能

为了测试PK算法的性能, 我们选取了10个常用的测试函数如表1所示, 并在不同的维度与迭代次数下对PK算法做精度测试并与带惯性权重的粒子群算法运算结果相比较. 其中, PK算法中 ${w_1} = 0.5$ , ${w_2} = 0.7$ , 粒子群算法中 $w = 0.5$ , ${c_1} = {c_2} = 2$ (该参数下性能较好), 速度的上下界设定为个体上下界的20%. 表2是两种算法的在30次独立运算下的平均值、最小值及标准差.

表 1 基准函数

基准函数	定义域	$\scriptstyle {f_{\min }}$
$\scriptstyle {f_1}(x) = \sum\limits_{i = 1}^n {{x_i}^2} $	[–100, 100]ⁿ	0
$\scriptstyle {f_2}(x) = \sum\limits_{i = 1}^n {\left\| {{x_i}} \right\|} + \mathop \Pi \limits_{i = 1}^n \left\| {{x_i}} \right\|$	[–10, 10]ⁿ	0
$\scriptstyle {f_3}(x) = \sum\limits_{i = 1}^n {(\sum\limits_{j = 1}^i {{x_j}){}^2} } $	[–100, 100]ⁿ	0
$\scriptstyle {f_{{4}}}(x) = \max \left\{ {\left\| {{x_i}} \right\|, 1 \leqslant i \leqslant n} \right\}$	[–100, 100]ⁿ	0
$\scriptstyle {f_{{5}}}(x) = \sum\limits_{i = 1}^{n - 1} {[100{{({x_{i + 1}} - {x_i}^2)}^2} + (1 - {x_i}){}^2]} $	[–30, 30]ⁿ	0
$\scriptstyle {f_6}(x) = \sum\limits_{i = 1}^n {{{\left\lfloor {{x_i} + 0.5} \right\rfloor }^2}} $	[–100, 100]ⁿ	0
$\scriptstyle {f_7}(x) = \sum\limits_{i = 1}^n {i \cdot {x_i}^4 + random[0, 1)} $	[–1.28, 1.28]ⁿ	0
$\scriptstyle {f_8}(x) = \sum\limits_{i = 1}^n {[{x_i}^2 - 10\cos (2\pi {x_i}) + 10]} $	[–5.12, 5.12]ⁿ	0
$\scriptstyle {f_9}(x) = - 20\exp [ - 0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{x_i}^2} } ] - \exp [\frac{1}{n}\sum\limits_{i = 1}^n {\cos (2\pi {x_i})} ] + 20 + e$	[–32, 32]ⁿ	0
$\scriptstyle {f_{10}}(x) = \frac{1}{{4000}}\sum\limits_{i = 1}^n {{x_i}^2} - \mathop \Pi \limits_{i = 1}^n \cos (\frac{{{x_i}}}{{\sqrt i }}) + 1$	[–600, 600]ⁿ	0

表 1 基准函数

竞争算法由于明确的目的性—提高适应度, 以及强化的学习性—在原有的基础上向强者学习, 因此收敛速度更快, 而且因为被挑战者的选择是随机的, 学习方向也多了随机性, 因此全局搜索能力能强. 从表2可以看出, PK算法对10个测试函数的平均值全部优于粒子群算法或者达到了全局最优. 在高维空间中的优越性更加明显. 尤其是40维度下的 ${f_2}$ 、 ${f_{{3}}}$ 、 ${f_{{6}}}$ 、 ${f_{{9}}}$ 四个函数的, 粒子群算法的收敛性能并不好, 但PK算法均能得到较好的优化结果. 对于30次试验中搜索到的最小值, 通过比较也可以发现, 除了10维度下的 ${f_{{2}}}$ 函数以及5维度下的 ${f_{{5}}}$ 函数略逊于粒子群算法, PK算法在这10个函数两种维度下搜索到的最小值亦全部优于粒子群算法或者找到了全局最优, 其中有多个函数都能收敛到全局最优0. 关于标准差, 除了40维时的 ${f_{{4}}}$ 函数, 其余函数下PK算法的标准差均小于粒子群算法的标准差. 因此说明PK算法的优越性在数量级上较粒子群效果显著, PK算法的收敛速度更快, 全局搜索能力更强, 且稳定性更好.

表 2 PSO和PK对比实验结果

函数	维数	迭代次数	平均值		最小值		标准差
函数	维数	迭代次数	PSO	PK	PSO	PK	PSO	PK
f₁	10	500	1.8024e–24	6.1258e–28	4.5260e–28	2.5244e–29	4.1118e–24	2.2645e–28
f₁	40	1500	5.2491e–12	2.3981e–29	3.6674e–14	0	7.2885e–12	3.2025e–29
f₂	10	500	7.3064e–15	7.0351e–15	1.7767e–16	1.4108e–15	1.2851e-14	4.5040e–15
f₂	40	1500	9.0000	8.9811e–17	2.1636e–09	1.1179e–17	9.5953	1.6728e–16
f₃	10	500	2.0728e–07	6.8170e-13	1.2153e-09	1.1370e–14	4.1393e–07	1.3503e–12
f₃	40	1500	1.2687e+03	2.0072	108.4506	0.2936	2.2788e+03	1.3764
f₄	10	500	3.4276e–07	4.6886e–12	1.3395e–08	1.6596e–12	3.0889e–07	2.5793e–12
f₄	40	1500	4.3305	4.1950	2.4801	2.0889	0.9005	1.3377
f₅	2	500	1.4753e–16	6.1302e–28	4.9070e–22	0	3.1270e–16	1.6563e–27
f₅	5	1000	0.2162	0.1682	0.0017	0.0612	0.7174	0.0448
f₆	10	500	0	0	0	0	0	0
f₆	40	1500	0.1667	0	0	0	0.7466	0
f₇	10	500	0.0026	0.0022	7.7620e–04	5.6941e–04	0.0013	9.8566e–04
f₇	40	1500	0.1086	0.0206	0.0119	0.0108	0.4912	0.0052
f₈	10	500	16.8479	3.0180	2.9849	0	6.2923	1.6829
f₈	40	1500	150.2999	23.6137	102.4805	15.9193	32.8736	4.5176
f₉	10	500	3.6563e–13	8.8226e–15	7.9936e–15	4.4409e–15	4.3780e–13	5.2516e–15
f₉	40	1500	0.0432	7.9936e–15	8.1207e–08	7.9936e–15	0.2367	0
f₁₀	10	500	0.0773	0.0126	0.0246	0	0.0269	0.0197
f₁₀	40	1500	0.0092	0.0013	2.4880e–13	0	0.0127	0.0030

表 2 PSO和PK对比实验结果

2.2 PK-BP神经网络算法性能

为了客观地验证和分析PK-BP神经网络算法的有效性, 选取了UCI数据集上的11组测试集测试了BP神经网络、PK-BP神经网络和用遗传算法优化的BP神经网络(GA-BP)的分类准确率. 他们分别是Balance-scale, Iris, Cancer, Blood-transfusion, Banknote authentication, Mammographic messes, Seeds, User Knowledge Modeling, Wireless Indoor Localization, Wine, Zoo. 这11组测试集的基本信息如表3所示. 将数据集中有缺失的样本删除, 然后随机抽取60%的样本用于训练, 余下40%的样本作为测试集.

表 3 数据集信息

作为比较, 对用遗传算法优化的BP神经网络(简记为GA-BP)进行仿真. 通过MATLAB R2016a分别用BP神经网络、PK-BP神经网络以及GA-BP神经网络对这11个数据集进行30次独立试验. 其中, 神经网络的训练次数均为5次, 学习速率为0.3, 训练目标最小误差为0.0001, 隐含层神经元个数为6, 传递函数为默认的正切S型及线性传递函数. GA和PK算法的种群规模为20, 迭代代数为50代, PK算法参数同前面, GA算法交叉概率为0.3, 变异概率为0.1. 实验结果如表4所示.

从表4可以看出, 在这11个数据集上, PK-BP与GA-BP算法的平均准确率均明显高于BP神经网络. 且PK-BP在8个测试集上平均值最高, GA-BP在剩下的3个测试集上平均值最高. PK-BP算法的分类正确率优越性明显, 比BP算法的正确率约提高了0.5%–7%. 从分类准确率的最大值这一项来看, BP算法有6次最大, PK-BP算法有9次最大, GA-BP有5次最大, 说明PK-BP算法的全局寻优能力最强; 从标准差来看, BP算法标准差最大, PK-BP和GA-BP均有6次达到最小, 说明PK-BP与GA-BP的稳定性都较好, 均优于BP神经网络. 综上可知, PK-BP神经网络分类正确率高, 寻优能力强, 且算法性能稳定.

3 结论与展望

本文提出了一种参数少、寻优能力强的竞争算法(PK), 通过10个测试函数验证了这种算法具有较好的全局搜索能力和稳定性. 并将该算法应入到优化BP神经网络中, 利用竞争算法的搜索能力有效提高了BP神经网络的精度及鲁棒性. 结果表明: PK-BP在11个测试集上的分类正确率更高, 稳定性更好. 尽管竞争算法已显示出其优越性, 但算法尚未完善, 可开发能力还很高, 在优化神经网络时以计算时间为代价, 下一步工作将对竞争算法的性能及应用进一步进行研究.

表 4 30次试验的正确率

参考文献

[1]	Lee HKH. Model selection for neural network classification. Journal of Classification, 2001, 18(2): 227-243.
[2]	张兴国, 刘晓磊, 李靖, 等. BP神经网络下的限速交通标志实时检测识别. 西安电子科技大学学报, 2018, 45(5): 136-142. DOI:10.3969/j.issn.1001-2400.2018.05.022
[3]	谢文兰, 石跃祥, 肖平. 应用BP神经网络对自然图像分类. 计算机工程与应用, 2010, 46(2): 163-166. DOI:10.3778/j.issn.1002-8331.2010.02.049
[4]	马峻, 赵飞乐, 徐潇, 等. MRA-PCA-PSO组合优化BP神经网络模拟电路故障诊断研究. 电子测量与仪器学报, 2018, 32(3): 73-79.
[5]	史丽萍, 汤家升, 王攀攀, 等. 采用最优小波树和改进BP神经网络的感应电动机定子故障诊断. 电工技术学报, 2015, 30(24): 38-45. DOI:10.3969/j.issn.1000-6753.2015.24.006
[6]	吴俊利, 张步涵, 王魁. 基于Adaboost的BP神经网络改进算法在短期风速预测中的应用. 电网技术, 2012, 36(9): 221-225.
[7]	Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0
[8]	蒋锋, 彭紫君. 基于混沌PSO优化BP神经网络的碳价预测. 统计与信息论坛, 2018, 33(5): 93-98. DOI:10.3969/j.issn.1007-3116.2018.05.014
[9]	高玉明, 张仁津. 基于遗传算法和BP神经网络的房价预测分析. 计算机工程, 2014, 40(4): 187-191. DOI:10.3969/j.issn.1000-3428.2014.04.036
[10]	洪延武, 刘双宇, 徐春鹰, 等. 基于多种群遗传算法与神经网络的激光-电弧复合焊接焊缝形貌预测. 应用激光, 2015, 35(6): 677-683.
[11]	韦鹏宇, 潘福成, 李帅. 改进人工蜂群优化BP神经网络的分类研究. 计算机工程与应用, 2018, 54(10): 158-163. DOI:10.3778/j.issn.1002-8331.1612-0379
[12]	黄亚驹, 陈福集, 游丹丹. 基于混合算法和BP神经网络的网络舆情预测研究. 情报科学, 2018, 36(2): 24-29.
[13]	郭彤颖, 陈露. 基于鸟群算法优化BP神经网络的热舒适度预测. 计算机系统应用, 2018, 27(4): 162-166.
[14]	徐小平, 师喜婷, 钱富才. 基于猴群算法求解0-1背包问题. 计算机系统应用, 2018, 27(5): 133-138. DOI:10.15888/j.cnki.csa.006340
[15]	田海霖, 洪良, 王艺翔, 等. 于量子遗传算法优化粗糙-Petri网的电网故障诊断. 西安工程大学学报, 2018, 32(6): 678-684.
[16]	陈龙, 张春雷, 赵成龙, 等. 一种求解7自由度机器人逆运动学的混合粒子群优化算法. 机器人, 2019. DOI:10.13973/j.cnki.robot.180489
[17]	Ratnaweera A, Halgamuge SK, Watson HC. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 240-255. DOI:10.1109/TEVC.2004.826071
[18]	卢滢宇, 王冰, 李学文, 等. 深层加速搜索的蜂群算法. 算机应用研究, 2012, 29(12): 4445-4447. DOI:10.3969/j.issn.1001-3695.2012.12.009
[19]	赵新超, 刘国莅, 刘虎球, 等. 基于非均匀变异和多阶段扰动的粒子群优化算法. 计算机学报, 2014, 37(9): 2058-2070.