元胞自动机模型(Cellular Automaton, CA)作为一种实现规则简单, 可以将复杂系统简单化的模型, 是目前应用最广泛的疏散模型之一[1]. 然而, 其简单的实现规则也导致了其在描述疏散个体行为上具有一定的局限性, 而且当元胞的邻域为扩展Moore邻域时, 会花费较多的时间用于搜索可行领域元胞.
人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)作为一种较为新型的群集智能算法, 其利用群体之间信息交互来实现全局寻优的思想, 为微观疏散模型的研究提供了一种新的思路. Lu DJ等人[2,3]使用人工鱼群算法来描述应急疏散时个体在路网中寻找疏散出口的过程.
不同于应急疏散, 在综合交通枢纽常规疏散的过程中, 人员的行为表现更为丰富, 具有排队等待、逗留、从众、跟随、随机探索、出(入)口选择行为、导向行为等, 使用单一的CA模型或者原始的AFSA算法都是难以完全刻画这些行为的. 因此, 本文改进原始AFSA算法, 结合CA模型, 提出一种基于元胞鱼群算法(CA-IAFSA)的人员疏散模型, 在刻画人员多样行为的同时, 降低模型的时间复杂度.
1 相关研究CA模型是把空间和时间按照一定间距离散化, 系统物理量只取有限个状态的物理系统简化模型[1]. 它具有四个基本组成部分: 元胞、状态、邻域和转换规则. 基于CA的疏散模型侧重于研究应急情况下的人员疏散过程[4–6], 关注于人员特性或者环境对疏散效率造成的影响[7–10], 忽略个体在疏散过程中的行为表现和相互影响.
AFSA算法最早是在2002年被提出的[11], 该算法使用人工鱼的四种基本行为: 聚群行为、追尾行为、觅食行为、随机行为来实现变量在变量空间中寻优的过程[12]. 该算法在解决配电网重构等一系列连续性优化问题取得了较好的效果, 但在解决离散型优化问题上仍具有一定的局限性[13].
目前, 将AFSA算法和CA结合起来进行研究的文献较少. 柳毅[14]在研究带时间窗可回程取货车辆路径问题数据模型的基础上, 将AFSA算法和CA结合设计了元胞鱼群算法. 将二者结合起来, 一方面可以提高AFSA算法对离散型优化问题的处理能力, 另一方面可以使用AFSA算法中人工鱼的搜索规则来替代CA模型中的元胞状态转换规则, 从而降低模型的时间复杂度.
2 基于元胞鱼群算法的疏散模型将综合交通枢纽内需要换乘的人员看成是人工鱼, 按照乘车意向划分为多个种群, 上层采用改进的AFSA算法, 底层采用CA框架, 将搜索空间离散化, 在每轮迭代过后, 利用CA模型的邻域模型和状态转换规则, 解决位置冲突.
2.1 模型假设(1)人员在移动过程中, 不考虑碰撞与挤压;
(2)换乘客流全部来源于火车到站客流, 其乘车意向假设已知. 人员在移动过程中不会更改乘车意向.
2.2 个体抽象考虑个体的速度差异、视野差异, 个体表示为:
| $p = \{ X,O,{v_0},w,M,Q\} $ | (1) |
其中, X代表个体
(1)出(入)口选择行为:
| $X_i^{t + 1} = X_i^t + \frac{{{e_O} - X_i^t}}{{||{e_O} - X_i^t||}} \times v(t)$ | (2) |
| ${e_O} = \arg \min T({E_k})$ | (3) |
| $T = \sum\limits_{j = 1}^n {t(j) + \frac{{d({E_k},{X_i}^t)}}{{{v_0}}}} $ | (4) |
其中,
(2)导向行为: 当在视野可见范围内, 没有目标出口, 存在引导指示时, 选择距离最近的引导指示
若
| $M = \{ {l_1},{l_2},\cdots,{l_k},l\} $ | (5) |
若
| $X_i^{^{{\rm{t}} + {\rm{1}}}} = X_i^t + \frac{{st - X_i^t}}{{||st - X_i^t||}} \times v(t)$ | (6) |
若
| $X_i^{t + 1} = X_i^t + \frac{{en - st}}{{||en - st||}} \times v(t)$ | (7) |
其中,
若
| $X_i^{t + 1} = \frac{{{l_k}(en) - {l_k}(st)}}{{||{l_k}(en) - {l_k}(st)||}} \times v(t)$ | (8) |
当
(3)从众行为:
| $S\_X_i^{t + 1} = X_i^t + \frac{{{X_c} - X_i^t}}{{||{X_c} - X_i^t||}} \times v(t)$ | (9) |
(4)跟随行为:
| $F\_X_i^{t + 1} = X_i^t + \frac{{{X_j} - X_i^t}}{{||{X_j} - X_i^t||}} \times v(t)$ | (10) |
(5)探索行为: 个体在视野范围内随机而不重复的任选一个位置
| $P\_X_i^{t + 1} = X_i^t + \frac{{{X_r} - X_i^t}}{{||{X_r} - X_i^t||}} \times v(t)$ | (11) |
若
(6)随机行为: 当
完成一轮迭代后, 最终确定下一时间步的移动位置
| $Q = ({e_O},{t_{}},{t_2})$ | (12) |
| ${t_2} = t + \sum\limits_{j = 1}^n {t(j)} $ | (13) |
当个体确定了下一个时间步的移动位置
(1)将
(2)当发生冲突时, 遍历
(3)
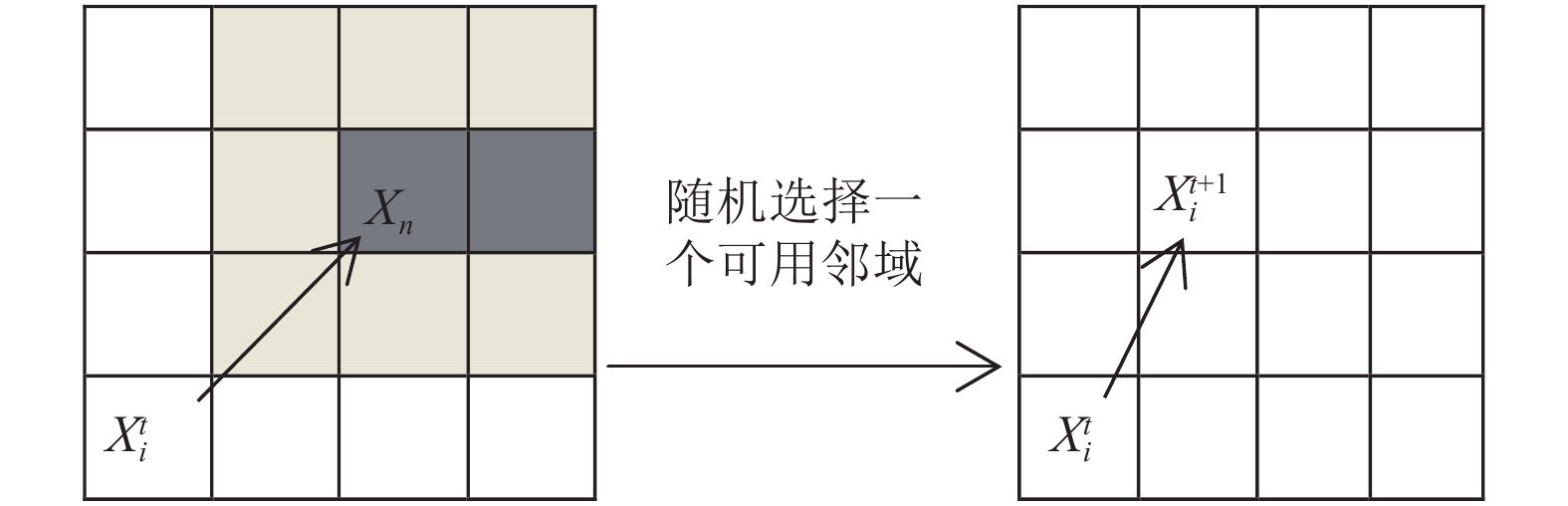
|
图 1 CA模型解决位置冲突 |
3 实验及结果分析 3.1 环境设置
在MATLAB上搭建2D模拟环境, 进行实验. 疏散环境设置如下:
(1)环境区域为
(2)这里参考文献[15], 设置个体占地面积
(3)
| 表 1 各交通方式的出/入口参数设置 |
3.2 算法参数分析
采用控制变量法依次测试人工鱼的探索尝试次数
(1)调试

|
图 2 参数
|
(2)调试
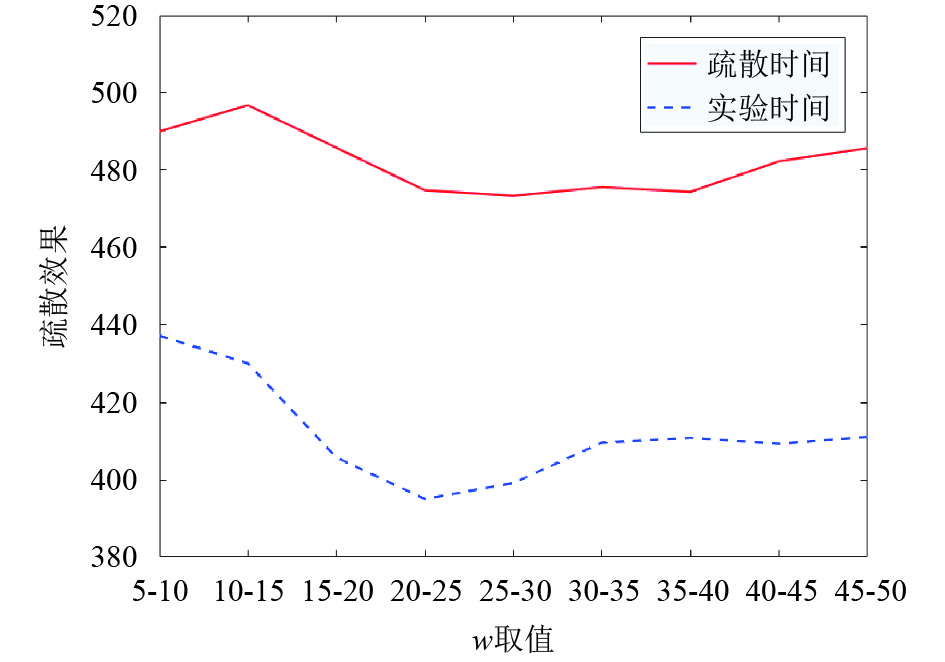
|
图 3 参数
|
从图2可知, 当设定人工鱼的视野范围
从图3中可知, 当设定人工鱼的探索尝试次数
设置人数为500, 换乘其他4种交通方式的人数各占25%. 对比三种模型: ① ICA模型: 在CA模型中, 加入导向行为、排队行为和出口选择机制; ② CA-AFSA: 将CA模型和原始AFSA模型结合, 加入排队行为和出口选择机制, 不加导向行为; ③ 本文提出的CA-IAFSA模型. (注: 由于完整截取的图片较大, 图4中的(c)和(d)只截取了部分效果图.)
对比图4中的(a)和(b)可以发现, 模型①中, 位于火车站内的绝大数个体“绝对理性地”选择了距离出口最近的位置, 紧贴靠近出口的障碍物进行移动, 且趋向于在出口处形成“拱形”. 而在模型③的模拟效果图中, 人群是从远离出口的初始位置以聚集的趋势逐渐向三个出口靠近, 有效地避免了“紧贴墙壁行走”. 模型③相比模型①更好地体现了“从众”和“避障”行为.
对比图4中的(c)和(d), 相比模型②, 加入“导向行为”的模型③克服了根据“最短路径原则”移动而陷入局部最优, 原地徘徊而无法继续疏散的缺陷, 实现了人群自发有序地向着目的换乘点移动, 很好地体现了人员疏散的“导向”行为.
对比图5中的(a), (b), 对于距离较近的三个火车出口, 模型③相比模型①, 实现了资源的均衡利用, 比较符合实际情况下人员的“出口选择”行为.
为了进一步验证CA-IAFSA模型的在疏散模拟时间性能上的提升, 分别将人数设置为300人, 500人, 1000人, 在同等条件下, 使用ICA模型和CA-IAFSA模型进行10次模拟实验取均值, 结果如表2所示.
由表2可以看出, 在同一实验条件下, 模型③与模型①相比, 平均疏散时间在一定程度上有所降低, 在实验时间花费上至少降低了59%. 原因是: 前者采用扩展型摩尔型邻域, 遍历邻域元胞获得下一个移动位置时花费了大量的时间. 后者采用AFSA算法中人工鱼的搜索规则来替代CA模型中的元胞状态转换规则, 避免了盲目搜索, 同时, 在一定程度上避免了“快即是慢”现象的发生, 防止人群由于“最短路径原则”产生过度拥挤, 从而提升疏散性能.

|
图 4 三种模型的模拟效果 |
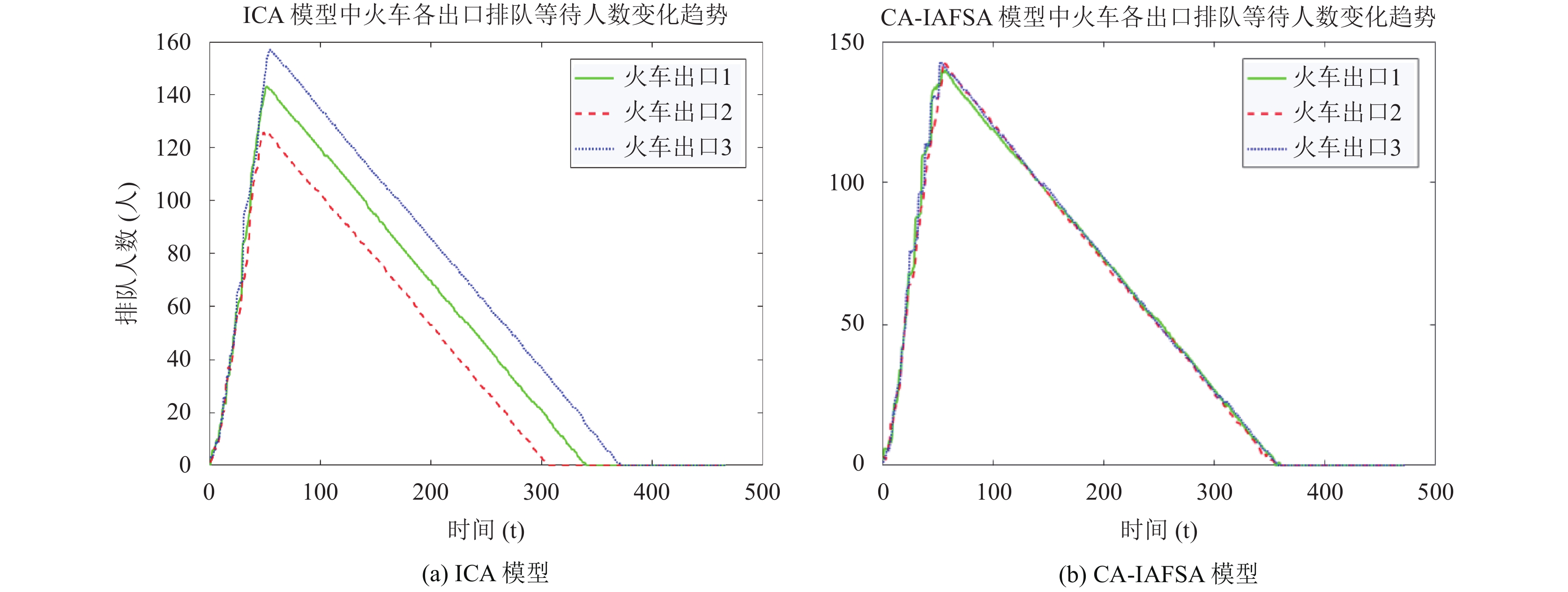
|
图 5 两种模型的火车出口排队人数变化趋势 |
| 表 2 两种模型的疏散效果对比 |
4 结论与展望
本文提出的CA-IAFSA模型, 针对综合交通枢纽的常规疏散, 考虑个体之间的速度差异、视野差异, 将导向行为和排队机制加入原始AFSA算法中, 融合CA模型构建人员常规疏散模型. 实验结果证明, CA-IAFSA模型, 可真实的反映人员在综合交通枢纽内进行换乘时的疏散过程. 克服了原始AFSA在存在障碍物的疏散环境中, 易陷入局部最优的缺陷, 在刻画人员的导向行为、避障行为、排队行为、出(入)口选择行为上具有较好的模拟效果, 相比ICA模型, CA-IAFSA模型在一定程度上减少了疏散时间, 在时间复杂度上至少降低了59%. 在今后的研究中, 会根据实际情况, 进一步对模型参数进行调整, 为特定综合交通枢纽场景中的人员常规疏散提供决策辅助.
| [1] |
Bakar NAA, Majid MA, Ismail KA. An overview of crowd evacuation simulation. Advanced Science Letters, 2017, 23(11): 11428-11431. DOI:10.1166/asl.2017.10298 |
| [2] |
Zong XL, Jiang YL, Wang CZ. Evacuation behaviors and link selection strategy based on artificial fish swarm algorithm. Proceedings of the 7th International Conference on Cloud Computing and Big Data. Macau, China. 2016. 279–283.
|
| [3] |
Lu DJ, Zhang GJ, Liu YL, et al. AFSA based path planning method for crowd evacuation. Journal of Computational Information Systems, 2014, 11(11): 3815-3823. |
| [4] |
张鑫龙, 陈秀万, 李怀瑜, 等. 一种改进元胞自动机的人员疏散模型. 武汉大学学报•信息科学版, 2017, 42(9): 1330-1336. |
| [5] |
杨波, 陈丹丹, 夏颖, 等. 基于GIS的CA-PSO多出口场景疏散模型研究. 中南民族大学学报(自然科学版), 2017, 36(1): 107-112. |
| [6] |
袁野, 田中旭. 隧道火灾疏散模型实时仿真算法的实现. 计算机工程与应用, 2017, 53(23): 208-211. DOI:10.3778/j.issn.1002-8331.1606-0083 |
| [7] |
李世威, 王建强, 刘应东. 初始分布非均匀的行人流疏散仿真研究. 计算机应用研究, 2017, 34(3): 702-705. DOI:10.3969/j.issn.1001-3695.2017.03.014 |
| [8] |
Fu ZJ, Zhou XD, Zhu KJ, et al. A floor field cellular automaton for crowd evacuation considering different walking abilities. Physica A: Statistical Mechanics and Its Applications, 2015, 420: 294-303. DOI:10.1016/j.physa.2014.11.006 |
| [9] |
蒋雪玲, 潘颖. 大规模聚集人群的疏散仿真模型研究. 计算机仿真, 2015, 32(6): 398-402, 415. DOI:10.3969/j.issn.1006-9348.2015.06.088 |
| [10] |
Zhong W, Tu R, Yang JP, et al. Simulation of evacuation process in a supermarket with cellular automata. Procedia Engineering, 2013, 52: 687-692. DOI:10.1016/j.proeng.2013.02.207 |
| [11] |
李晓磊, 邵之江, 钱积新. 一种基于动物自治体的寻优模式: 鱼群算法. 系统工程理论与实践, 2002, 22(11): 32-38. DOI:10.3321/j.issn:1000-6788.2002.11.007 |
| [12] |
Neshat M, Adeli A, Sepidnam G, et al. A review of artificial fish swarm optimization methods and applications. International Journal on Smart Sensing and Intelligent Systems, 2017, 5(1): 107-148. |
| [13] |
Neshat M, Sepidnam G, Sargolzaei M, et al. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artificial Intelligence Review, 2014, 42(4): 965-997. DOI:10.1007/s10462-012-9342-2 |
| [14] |
柳毅, 沈勤. 带时间窗可回程取货车辆路径问题的元胞鱼群算法. 系统管理学报, 2011, 20(6): 739-743. |
| [15] |
杨立中. 建筑内人员运动规律与疏散动力学. 北京: 科学出版社, 2012.
|
 2019, Vol. 28
2019, Vol. 28


