我国是世界上洪水灾害频繁且严重的国家之一,洪水灾害不仅范围大、发生频繁、突发性强, 而且损失大. 特别是近年来, 受全球气候变化和人类活动影响, 极端天气事件和人为突发水事件明显增加. 为了防治洪涝灾害, 我国投入了大量的人力、财力与物力,建设了一批又批防洪工程, 大大加强了我国抗灾御洪的能力. 与此同时, 我国还加强了非工程防洪措施. 其中, 洪水预报就是预防洪水灾害的重要非工程措施之一, 也一直是专家学者关心的课题. 因此提高洪水预测的准确性, 减轻洪水带来的一系列灾害, 对整个流域的防洪安全有着非常重要的意义. 一般来说洪水预测有3种不同的方法, 经验法、统计法以及模型方法, 但水文系统中多变量之间的非线性关系[1]远非传统方法能解决. 随着科学技术的快速发展, 如何把最新的科学技术引入到水文预报中, 提高水文预报精度, 成为大家的关注点. 随着人工神经网络[2]等非线性科学技术在各个行业的广泛应用, 为解决上述问题提供了机遇.
目前国内已有很多学者尝试将人工神经网络引入到洪水预测中. 兰州理工大学的李晓丽等[3]提出了不确定, 确定支持向量机在洪水预测模型中的应用, 该算法利用数据间的关系去掉冗余的信息, 简化算法运算, 从而提高了洪水预测的精度; 晋中市水文水资源勘测局的梁存峰等[4]提出了基于混沌自适应模型在洪水预测中的研究, 该模型亦可在数据较少的情况下, 取得精度较好的预测结果; 福建省南平市水利局的金保明[5]在闽江十里庵流量预测中应用BP神经网络, 将反向传播BP神经网络模型应用于洪水预测, 并且预测精度符合要求; 何勇、李妍琰[6]提出改进粒子优化 BP神经网络的洪水智能预测模型研究, 以BP神经网络为基础, 提取水位站往年平均径流量作为洪水属性, 采用POS算法对BP神经网络的各个参数进行优化, 得出最优的 BP神经网络预测适应度值, 提高了预测的效率. 以上算法都是比较传统的神经网络算法, 虽然在一定程度上提高了洪水预测精确度, 但是精度依旧不是特别理想.
本文提出一种基于正则化GRU神经网络的洪水预测模型来提高洪水预报精度, 选用relu函数作为整个神经网络的输出层激活函数[7–9], 将弹性网正则化引入到GRU模型中, 对网络中输入权重w实施正则化处理, 以提升GRU模型的泛化性能. 并将该模型应用于外洲水文站每月平均水位的拟合及预测, 实验对比表明, 弹性网正则化改进后模型的拟合效果和预测效果明显提高, 该方法计算出的均方根误差较小, 预测拟合程度较高.
1 GRU模型简介传统的人工神经网络又被称为前馈神经网络 FNN, 是一种最简单的神经网络, 包含输入层、隐藏层这种模型在处理序列数据时只能利用当前时刻的信息, 无法利用历史信息. Elman在1990年提出了循环神经网(Recurrent Neural Network, RNN), 其隐藏层之间的节点也是有连接的, 因此隐藏层的输入不仅包括当前时刻输入层的输入还包括上一时刻隐藏层的输出. 理论上, RNN能够对任何长度的序列数据进行处理, 但是在实践中, 当相关信息和当前预测位置之间的间隔不断增大时, RNN就会丧失学习远距离信息的能力. 这是因为RNN通常使用的是BPTT反向传播算法对网络进行优化, 但是BPTT无法解决长时依赖问题, 因此该算法会带来神经网络梯度消失问题和梯度爆炸问题.
为了解决RNN网络的梯度消失和梯度爆炸问题, 研究人员在优化学习算法和配置网络的技巧方面提出了较多的改进方法. 文献[10,11]中介绍 Schimidhuber H于1997年提出了长短期记忆单元(Long Short-Term Memory, LSTM), 用于改进传统的RNN模型. LSTM神经单元是由一个或多个存储器外加三个自适应乘法门组成. 它通过输入门、输出门和遗忘门来控制信息的流动和传递, 通过对输入的信息进行剔除或增强到神经细胞单元中实现对细胞状态的控制, 使得LSTM可以记忆、更新长距离的信息, 从而实现对长距离信息的处理. 受LSTM模型门机制启发, Stanford在2014年提出了GRU模型, GRU网络将LSTM结构中的输入门和遗忘门结合成一个单独的更新门, 合并了记忆细胞和隐含状态, 同时也做了一些调整. 已有研究结果表明, GRU模型的性能与LSTM相当, 但计算效率更高, 参数更少. 整体的GRU神经网络结构如图1所示.

|
图 1 GRU神经网络结构示意图[5] |
GRU中各个门的表达式如下:
GRU更新门表达式:
| ${Z_t} = s\left( {{W_z} \bullet \left[ {{h_{t - 1}},{x_t}} \right]} \right)$ | (1) |
GRU重置门表达式:
| ${r_t} = s\left( {{W_r} \bullet \left[ {{h_{t - 1}},{x_t}} \right]} \right)$ | (2) |
GRU输出部分表达式:
| ${\tilde h_t} = \tanh \left( {{W_k} \bullet \left[ {{r_t} * {h_{t - 1}},{x_t}} \right]} \right)$ | (3) |
| ${h_t} = \left( {1 - {z_t}} \right) * {h_{t - 1}} + {z_t} * {\tilde h_t}$ | (4) |
| ${y_t} = s\left( {{W_0} \cdot {h_t}} \right)$ | (5) |
式(1)中
在深度神经网络中, 随着层数以及各层神经元个数的增加, 模型中参数的个数会以极快的速度增长. 当网络参数个数过多或训练数据集很小时, 神经网络模型往往会出现过拟合问题. 所谓过拟合, 就是模型在训练数据上拟合效果好, 但是它在验证集上效果很差, 即模型泛化能力差. 目前, 防止过拟合的一般方法是增大训练数据集, 但当数据集有限时, 防止过拟合的方法则是在训练数据集中加入正则化技术. 现在我们主要讨论一些旨在改善过拟合的正则化方法.
正则化的方法就是在模型cost函数中加入某种正则项或几种正则项的组合, 表达式如下:
| $\min \left\{ {\sum\limits_{t = 1}^T {l\left( {{y_t},f\left( {{x_t},w} \right)} \right) + \sum\limits_{i = 1}^m {{\lambda _i}{\rho _i}} } } \right\}$ | (6) |
式中,
本文将弹性网引入到GRU模型中, 对网络中输入权重w实施正则化处理, 以提升GRU模型的泛化性能, 模型如下:
| $\mathop {\min }\limits_w \left\{ {\frac{1}{T}{{\sum\limits_{t = 1}^T {\sum\limits_{j = 1}^m {\left( {{y_{ti}} - {{\bar y}_{ti}}} \right)} } }^2} + {\lambda _1}{\rm{||}}{{\rm{w}}_1}|| + {\lambda _2}{\rm{||}}{{\rm{w}}_2}|{|^2}} \right\}$ | (7) |
其中,
由于GRU在训练过程中, 容易出现过拟合现象, 而正则化方法通过限制网络中权重的大小, 可以对一些因子施加惩罚, 以够弥补网络本身的不足. 所以这里利用正则化方法来优化GRU模型, 从而实现对外洲站水位的预测. GRU改进模型构建步骤如下:
步骤1: 将时间序列的水文数据进行预处理, 采用极差法使数据标准化, 首先计算指标值的最小值和最大值, 然后计算极差, 通过极差法将指标值映射到[0–1]之间, 公式为:
| ${x^ * } = \frac{{x - \min }}{{\max - \min }}$ | (8) |
步骤2: 将时间序列水文数据集
| $X = \{ {X_1},{X_2},\cdots,X_L^{}\} $ | (9) |
| ${X_p}{\rm{ = }}\left\{ {{f_p},{f_{p + 1}},\cdots,{f_{m - L + p - 1}}} \right\}$ | (10) |
其中,
隐藏神经元的输出值定义公式为:
| ${\rm{y = }}W \cdot x + b$ | (11) |
X经过隐藏层后的输出可表示为:
| $Y{\rm{ = }}\left\{ {{Y_1},{Y_2},\cdots,{Y_L}} \right\}$ | (12) |
| ${Y_p}{\rm{ = }}\left\{ {{f_{p + 1}},{f_{p + 2}},\cdots,{f_{m - L + p}}} \right\}$ | (13) |
其中,
选用均方误差作为误差计算公式, 训练中的损失函数定义公式为:
| $loss = \frac{1}{n}\sum\limits_{t = 1}^n {{{({y_i} - {y_{real}})}^2}} $ | (14) |
损失函数是用来评估神经网络目标输出和实际输出差距的函数, 函数值越小说明实际输出与目标输出的差值越小, 也就说明权值越合适. 将损失函数与正则项之和设置为目标函数, 给定网络初始化的学习率以及训练步数, 如式(7)再应用Adam优化算法实现目标函数的最小化并不断更新网络权重, 从而得到最终的隐藏层网络.
步骤3: 预测过程采用迭代的方法. 理论输出P的最后一行数据:
| $P_f^{} = \{ {p_{m - L + 1}},{p_{m - L + 2}},\cdots,{p_m}\} $ | (15) |
将
| ${Y_f}{\rm{ = }}\{ {y_{m - L + 2}},{y_{m - L + 3}},\cdots,{y_{m + 1}}\} $ | (16) |
则m+1时刻的预测值为
| $P_{f + 1}^{}{\rm{ = }}\{ {p_{m - L + {\rm{2}}}},{p_{m - L + {\rm{3}}}},\cdots,{y_{m + 1}}\} $ | (17) |
将
| ${Y_0} = \{ {y_{m + 1,}},{y_{m + 2}}, \cdots ,{y_n}\} $ | (18) |
步骤4: 对
本实验环境为:硬件配置CPU i7-7700K, GPU Gtx1060, 运行内16 GB; 软件配置CUDA9.0、cudnn7.1; 操作系统Ubuntu16.04; 语言python3.6;框架tensorflow.
本实验的代码参数设置如下: 输入层神经元个数设为数设为3, 输出层神经元个数设为1, 其中的隐藏单元的数量选取为10, 每批数据量的大小batch_size设为10, 通过调节λ值得到三种正则化网络模型:
为了验证本文所验证的预测模型的可行性以及有效性, 本文所采用的精度评定标准来自于中华人民共和国水利部《水文情报预报规范》(SL250-2000)[17], 一次预报的误差小于许可误差时, 为合格预报. 合格预报次数与预报总次数的百分比为合格率. 本文结合《水文情报预报规范》的有关规定设置水位许可误差为0.2 m. 合格率QR的表达公式如下:
| ${\rm{QR}} = \frac{n}{m} \times 100\% $ | (19) |
其中, m是预报的总次数、n是合格预报(预报误差小于许可误差)的次数; 当QR
采用均方根误差RMSE(Root Mean Square Error)来定量的评价模型的预测性能, RMSE通过计算预测值对观察值的平均偏差程度来反映模型的预测性能, 值越小预测效果越好. 公式定义如下:
| $RMSE = \sqrt {\frac{{\sum\limits_{t = 1}^T {{{(\bar y_c^t - y_c^t)}^2}} }}{T}} $ | (20) |
通过对上文中每种模型结构及参数的确定, 共得到四种不同的GRU模型. 为了比较这四种网络模型预测性能, 将四种模型分别对外洲站水文数据做训练及预测, 每组的误差统计见表1.
| 表 1 几种预测模型RMSE值和合格率(QR)统计表 |
由表1可以看出3种正则化GRU模型的RMSE的值均比普通GRU模型的RMSE值小,
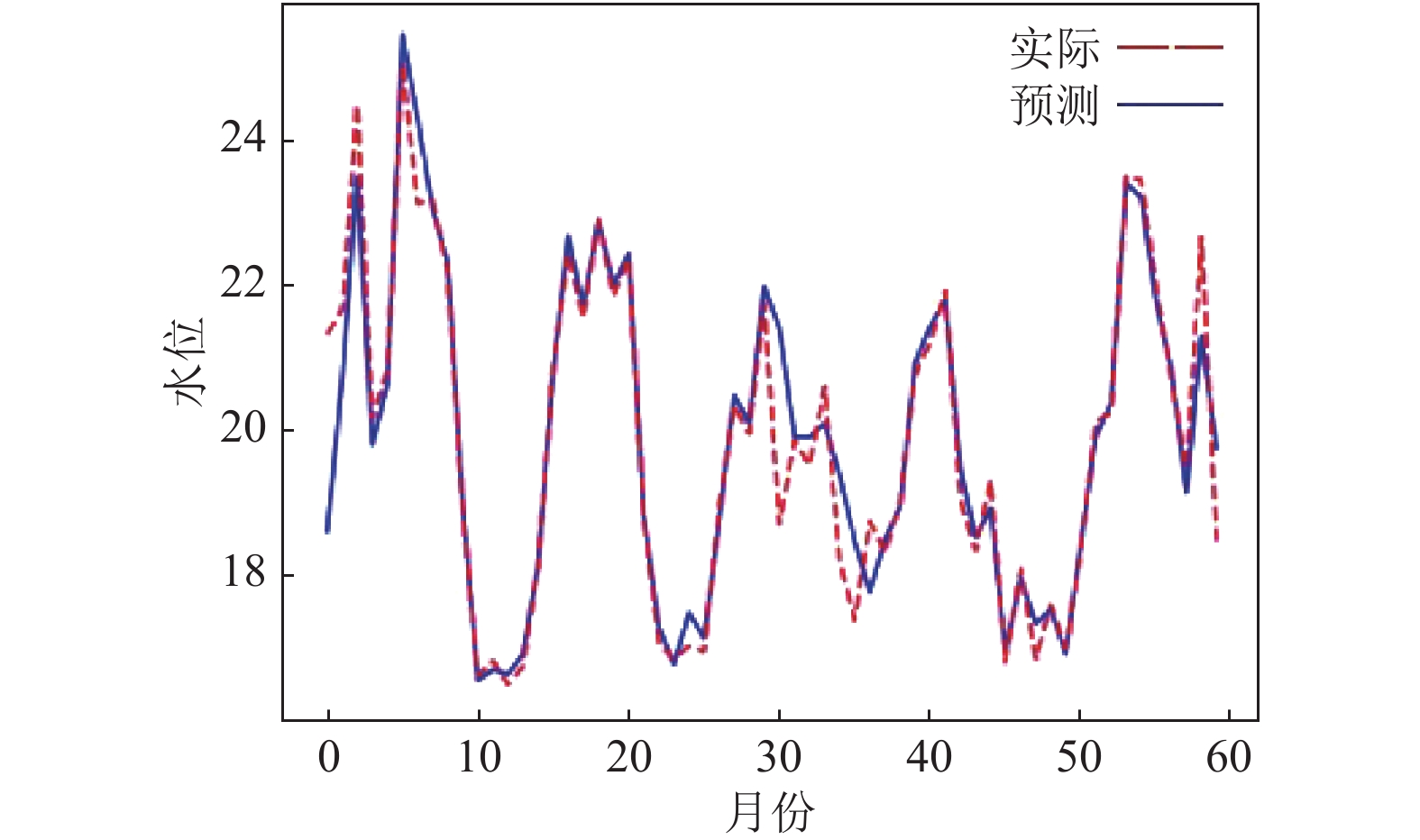
这里选取各自最小RMSE的实验预测结果图, 如图2–图5所示.
|
图 2 GRU模型预测结果图(
|
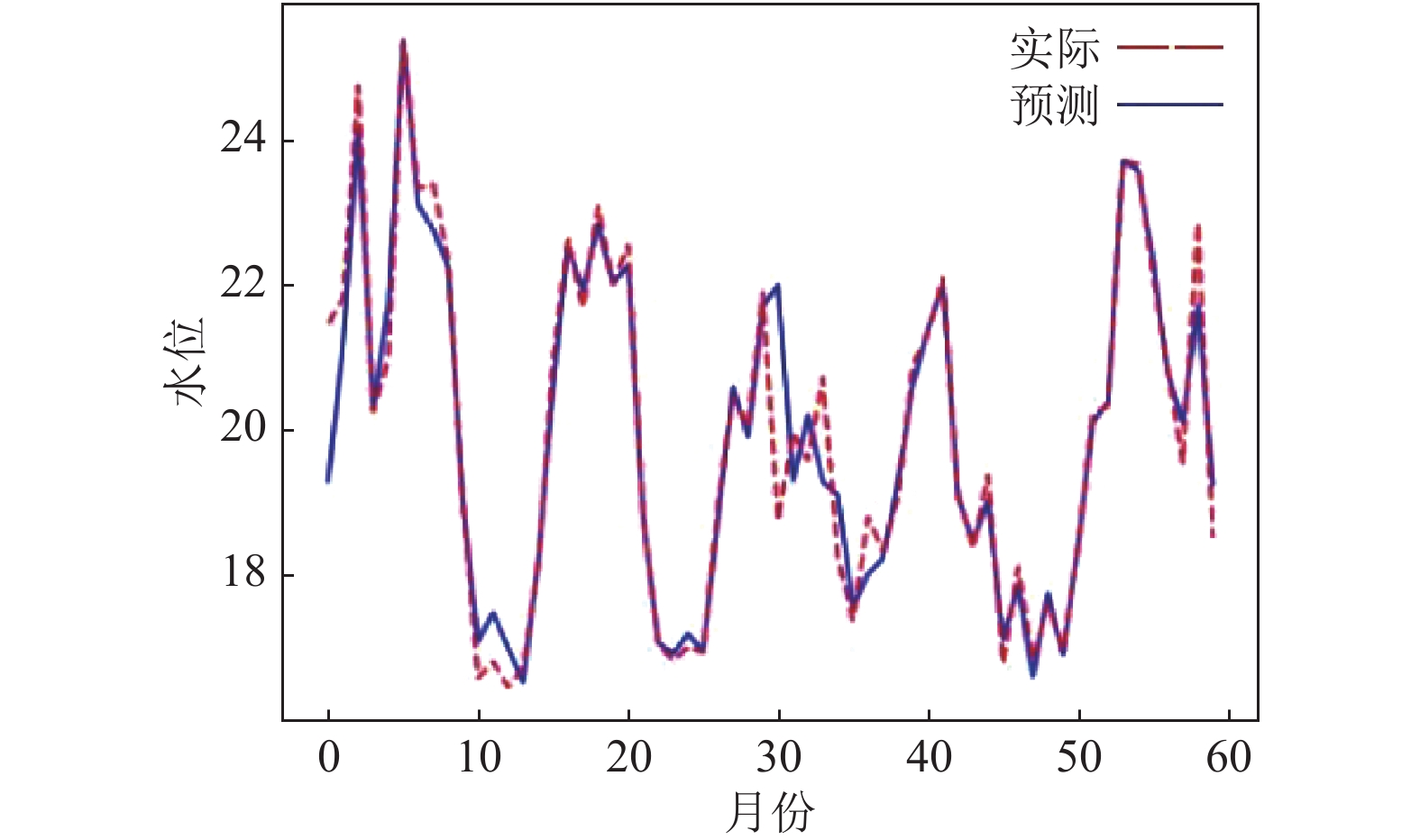
|
图 3 |
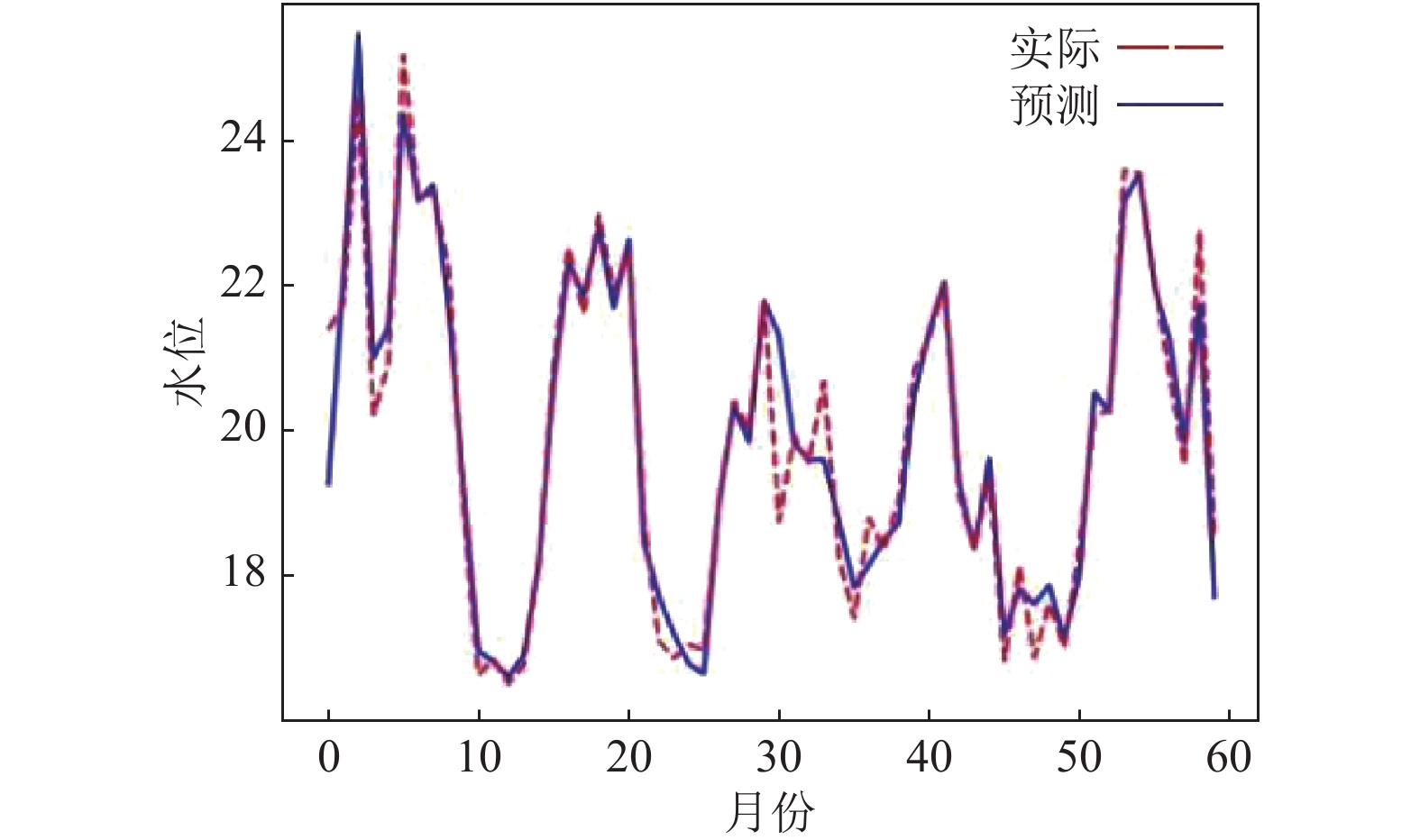
|
图 4 |

|
图 5 弹性网正则化网络预测结果图(
|
4 结论
本文使用正则化GRU模型对水文站往年每月平均水位进行预测, 通过比较三种正则化方法对GRU模型的改进, 发现用弹性网正则方法优化GRU模型后合格率提高了9.3%, 预测精度从乙等升到了甲等. 由于洪水预测受到多方因素以及突发因素的影响, 本文所使用的神经网络训练数据资料有限导致模型预测精度不是非常高, 有待结合更多相关影响因子来进行研究处理.
| [1] |
范睿. 基于遗传算法的神经网络洪水预报研究与应用[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2005.
|
| [2] |
Lippmann RP. An introduction to computing with neural nets. ACM SIGARCH Computer Architecture News, 1988, 16(1): 7-25. DOI:10.1145/44571 |
| [3] |
李晓丽, 周小健, 沈钢纲, 等. 不确定支持向量机在洪水预测模型中的应用. 兰州理工大学学报, 2012, 38(3): 107-110. DOI:10.3969/j.issn.1673-5196.2012.03.025 |
| [4] |
梁存峰. 基于混沌Volterra自适应模型的洪水预测研究. 水资源与水工程学报, 2011, 22(1): 146-150. |
| [5] |
金保明. BP神经网络在闽江十里庵流量预测中的应用. 水电能源科学, 2010, 28(9): 12-14. DOI:10.3969/j.issn.1000-7709.2010.09.004 |
| [6] |
何勇, 李妍琰. 改进粒子群优化 BP 神经网络的洪水智能预测模型研究. 西南师范大学学报(自然科学版), 2014, 39(5): 75-80. |
| [7] |
叶小舟, 陶飞飞, 戚荣志, 等. 循环神经网络结构中激活函数的改进. 计算机与现代化, 2016(12): 29-33. DOI:10.3969/j.issn.1006-2475.2016.12.006 |
| [8] |
Semeniuta S, Severyn A, Barth E. Recurrent dropout without memory loss. arXiv preprint arXiv:1603.05118, 2016.
|
| [9] |
刘洋. 基于GRU神经网络的时间序列预测研究[硕士学位论文]. 成都: 成都理工大学, 2017.
|
| [10] |
张玉环, 钱江. 基于两种LSTM结构的文本情感分析. 软件, 2018, 39(1): 116-120. DOI:10.3969/j.issn.1003-6970.2018.01.023 |
| [11] |
王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测. 北京航空航天大学学报, 2018, 44(4): 772-784. |
| [12] |
刘建伟, 崔立鹏, 刘泽宇, 等. 正则化稀疏模型. 计算机学报, 2015, 38(7): 1307-1325. |
| [13] |
崔东文. 多隐层BP神经网络模型在径流预测中的应用. 水文, 2013, 33(1): 68-73. DOI:10.3969/j.issn.1000-0852.2013.01.013 |
| [14] |
丁海蛟. 基于LS-SVM的河道洪水预报研究[硕士学位论文]. 昆明: 昆明理工大学, 2016.
|
| [15] |
孙卫刚, 王正勇. 克尔古提水文站站月水量预报方案的编制. 大科技·科技天地, 2010.
|
| [16] |
朱星明, 卢长娜, 王如云, 等. 基于人工神经网络的洪水水位预报模型. 水利学报, 2005, 36(7): 806-811. DOI:10.3321/j.issn:0559-9350.2005.07.007 |
| [17] |
中华人民共和国水利部. SL 250–2000 水文情报预报规范. 北京: 中国水利水电出版社, 2001.
|
 2019, Vol. 28
2019, Vol. 28


