2. 中国科学院 半导体研究所, 北京 100083;
3. 中国科学院大学, 北京 100049;
4. 中国科学院 脑科学与智能技术卓越创新中心, 上海 200031;
5. 半导体神经网络智能感知与计算技术北京市重点实验室, 北京 100083
2. Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai 200031, China;
5. Semiconductor Neural Network Intelligent Perception and Computing Technology Beijing Key Lab, Beijing 100083, China
军用无人机由于其造价成本低, 机动性能好, 可以减少人员伤亡等优点, 被大量用于执行不同的军事任务. 而成功执行任务的前提是无人机能够保证安全及时的达到指定目标区域. 这就需要在任务空间中, 为无人机规划出一条满足可行性、实效性、最优性的航迹[1]. 常用的航迹规划算法可分为经典算法和智能算法两大类[2]. 经典算法主要包括动态规划法、牛顿法、最优控制法等. 这些经典算法虽然算法简单, 但是计算时间会随着问题规模的变大而爆炸式的增长, 所以目前航迹规划最常用的还是智能规划算法.
智能算法主要有A*算法[3]、遗传算法[4]、蚁群算法[5]等. 这些算法虽然各有优点, 但若直接用它们的基本形式来求解航迹规划问题, 会存在各种各样的缺点, 比如搜索耗时长, 占用内存大, 容易陷入局部最优等等. 对此许多专家学者对它们进行了不同方面的改进工作. 文献[6]在A*算法的启发函数中加入了父节点的影响, 使算法的实时性得到了提高. 文献[7]通过指数衰减的方式对文献[6]提出的启发函数进行了加权, 使算法在搜索航迹时的节点遍历数目得到减少, 进而减少了内存的占用. 文献[8]使用了二叉堆的结构对A*算法中open表的管理进行了优化, 提高了算法的运行速度, 并对最终的航迹进行了平滑处理, 使之更适合无人机飞行. 文献[9]将基因对比度引入到遗传算法中, 用来增加优良基因遗传给下一代的概率, 提高了算法在航迹规划中的实时性. 文献[10]通过在遗传算法的群体进化过程中, 根据个体适应度值的大小来自动调节交叉概率和变异概率, 从一定程度上克服了算法早熟的缺点. 文献[11]将自适应阈值引入到蚁群算法中, 利用渐进减少的阈值对算法的搜索过程进行干涉, 降低了算法陷入局部最优的风险. 综合上述, 如何提高航迹规划算法的求解质量、时效性, 同时尽量减少算法耗用的内存空间, 是我们后续算法研究的出发点.
智能算法中的模拟退火算法[12]具有简单易实现、局部搜索能力强、在一定程度上能够摆脱局部最优解的特点. 但通常要得到更优化的解, 则需要耗费较长的收敛时间. 本文在对其进行设计与实现之后, 在初始解产生方式上, 引入了简化的稀疏A*算法, 进而得到了FSSA-SA算法, 并且对算法求解过程中的冗余节点进行了剔除. 相比于模拟退火算法, 新的FSSA-SA算法在求解速度和质量上, 都有所提升.
1 航迹规划问题建模 1.1 威胁建模无人机飞行环境中的威胁信息可以事先通过各种侦查手段来获得, 包括它们的位置, 影响范围等. 在此我们主要考虑静态情形下地形、高炮、雷达、导弹对无人机的威胁. 在航迹搜索的过程中, 通过有效避开这些威胁所影响的区域, 就可以大大提高无人机的生存率.
二维空间情况下, 对上述威胁建模的通常方法是先将其作用范围等效为圆, 威胁中心点等效为圆心, 再进一步建立无人机所受威胁概率p与它到该威胁中心的距离之间的函数关系[13]:
| $ p = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;(d \le {R_{\rm{min}}})\\ f(d)\;\;\;({R_{\rm{min}}} < d \le {R_{\rm{max}}})\\ 0\;\;\;\;\;\;\;\;\;({R_{\rm{max}}} < d) \end{array} \right. $ | (1) |
其中, d为无人机到威胁中心的距离, Rmin为必受威胁区半径, 对无人机而言属于禁飞区. Rmax为该威胁源所能影响的最大范围半径, 它与Rmin共同确定的圆环区域中, 以一定的概率存在着对无人机的威胁, 该威胁概率用函数f(d)表示. 当d大于Rmax时, 则认为无人机不受该威胁源的影响. 文献[13]中给出了雷达、导弹、高炮、地形四类威胁源的详细威胁模型, 并通过分析, 进一步简化得到了它们对应的威胁概率函数表达式:
| $ {p_M} = {p_A} = f(d) = 1/d $ | (2) |
| $ {p_R} = f(d) = 1/{d^4} $ | (3) |
| $ {p_T} = f(d) = \frac{{{R_{\rm{max}}} - d}}{{{R_{\rm{max}}} - {R_{\rm{min}}}}} $ | (4) |
其中, pM, pA, pR, pT分别对应导弹、高炮、雷达、地形的威胁概率. 可见, 随着距离d的增大, 无人机所受威胁也就越小.
1.2 无人机自身的约束在考虑航迹安全性的同时, 可行性也至关重要. 由于无人机自身携带的燃油有限, 因此要求我们规划出的航迹总航程要尽量的小, 必须满足在无人机最大航程范围以内. 另一方面, 受无人机最大转向角的限制, 要求我们规划出的航迹要尽量平滑.
1.3 综合代价函数综合代价函数是无人机面临的各类威胁与约束在飞行航迹上的集中反映. 我们通过它来衡量众多航迹的优劣或者某一空间位置的好坏. 这里我们给出综合代价E的函数表达式如下:
| $ E = \int_0^L {{a_1}{e_t} + {a_2}{e_l}ds = {a_1}{E_t} + {a_2}{E_l}} $ | (5) |
式中, L表示整条航迹. et和el分别对应每个微元航迹段上的威胁代价与油耗代价, a1, a2分别对应它们的权重系数. E表示综合代价, 它是威胁代价与油耗代价在整条航迹上的积分叠加值. Et和El分别为总威胁和总油耗代价.
由于在规划空间中, 我们用一系列离散节点来表示整条航迹, 因此可以对各相邻两个节点间的航迹段长度值进行求和, 再乘以油耗因子来得到总油耗代价:
| $ {E_l} = {\omega _l}\sum\limits_{i = 1}^{n - 1} {{l_{i,i + 1}}} $ | (6) |
式中的n为总航迹节点数, ωl是油耗因子, 代表航程向油耗代价转换的系数, li, i+1为航迹节点i和i+1之间的距离.
对于节点i和i+1所确定的航迹段, 在计算其威胁代价时, 为了简化计算, 我们使用航迹段上有限个节点的威胁代价累加, 来近似对整个航迹段的威胁代价积分运算. 借鉴文献[14]中的方法对航迹段进行取点, 即取它的4个五等分点和末端点i+1共5个节点. 在得到各航迹段的威胁代价后, 将它们累加一起, 就得到了整条航迹的总威胁代价:
| $ {E_t} = \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = 1}^5 {{P_{i,i + 1,j}}} } $ | (7) |
其中, Pi, i+1, j为所有威胁源在航迹段(i, i+1)上第j个节点处的威胁概率值叠加后的总和.
2 基于模拟退火算法的航迹规划 2.1 模拟退火算法基本原理模拟退火算法是对固体退火过程的近似模拟, 其基本思想如下: 首先, 给系统赋予一个初始状态, 同时将温度设定的比较高; 然后, 给与当前状态一个随机的扰动, 产生一个新的状态, 并通过前后两个状态的能量变化来判断是否接受该新状态. 对于系统能量减小的状态, 系统直接接受; 对于系统能量增加的状态则在高温时能够以很大概率接受, 后期随着系统温度的逐渐降低, 接受的可能性就越来越小, 直到不再接受.
在实际求解优化问题的运用中, 新生解的接受概率由Metropolis准则[15]得到:
| $ {P_t}({x_i} \to {x_{i + 1}}) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta E < 0\\ \exp ( - \beta \Delta E),\;\;\;\Delta E > 0 \end{array} \right. $ | (8) |
式中, Pt表示当前解xi转换到新解xi+1的概率. ΔE为新解对应的待优化目标函数值与原值之间的变化量. β对应温度的倒数. 当遇到使 ΔE大于0的新解时, 处理方式如下: 先产生一个在[0, 1)区间内均匀分布的随机数u, 如果它满足不等式
结合模拟退火算法的基本原理, 并参考文献[16]中的初始解产生方式, 我们给出如下的基本模拟退火算法:
(1) 设置起始温度倒数β0和终止温度倒数β1以及退火温度表长度nsweeps的值, 以
(2) 随机的在规划空间中产生连接起始点和终点的初始航迹, 计算相应的综合代价值, 并将β设置为起始值.
(3) 在当前温度下, 沿着从起点到终点的方向, 依次对除航迹起始点、终点以外的每一个中间节点进行扰动操作, 并计算该次扰动产生的新解对应的ΔE. 如果
(4) 如果对所有中间节点都完成了步骤(3)中所述操作, 则转步骤(5), 否则继续对剩余节点进行未完成的操作.
(5) 将温度表中的下一个值赋值给β, 并判断是否到达终止值β1, 若是则终止算法, 输出最终结果. 否则, 转步骤(3).
2.2.2 新解的产生以及ΔE的计算如何对当前解进行"细微扰动", 产生新的解. 我们给出如下的设计方法:

|
图 1 新解产生示意图 |
如图1所示, 在航迹段中, 设C是当前被选中需要更新位置的节点, A, B是它的两个相邻节点. 我们在与A、B节点连线垂直的两个方向中, 随机选择一个方向将节点C移动一小段距离ds, 并将移动后的节点与其他原航迹节点构成的航迹作为新产生的解. ds 的值在退火过程中, 会随着温度的降低而慢慢变小.
令A、B、C三个节点的坐标分别为(x1, y1)、(x2, y2)、(xold, yold), 则更新后的C节点位置(xnew, ynew)计算方式如下: 如果A、B间斜率存在, 则:
| $ \begin{array}{l} \left\{ \begin{array}{l} {x_{new}} = {x_{old}} \pm k \times b,\;\;\;\;\mu < 0.5{\text{时为}} + \\ {y_{new}} = {y_{old}} \mp b,\;\;\;\;\;\;\;\;\;\;\mu < 0.5{\text{时为}} - \; \end{array} \right.\\ \left\{ \begin{array}{l} k = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}\\ b = {d_s}\sqrt {\frac{1}{{{k^2} + 1}}} \end{array} \right. \end{array} $ |
如果A、B间斜率不存在, 则:
| $ \left\{ \begin{array}{l} {x_{new}} = {x_{old}} \pm {d_s},\;\;\;\;\mu < 0.5{\text{时为}}+\\ {y_{new}} = {y_{old}} \end{array} \right. $ |
其中, k为A、B节点间的斜率, b是为了简化公式引入的参数, μ为0到1之间均匀分布的随机数.
新解的产生带来了航迹综合代价的变化. 我们设原航迹段AC、CB对应的代价分别为e1和e2, 新航迹段的分别为e3和e4. 则:
| $ \Delta E = ({e_3} + {e_4}) - ({e_1} + {e_2}) $ | (9) |
可以看到, 我们只需要计算两个发生变化的航迹段的代价和的差, 就能得出整条航迹的综合代价变化量, 而不用先求出变化前后整条航迹的代价后再做差来得到.
3 模拟退火算法与简化稀疏A*算法的融合 3.1 FSSA-SA算法和简化的稀疏A*算法理想的模拟退火算法, 只要退火起止温度选择合适, 退火时间足够长, 初始解的选择对最终结果影响不大. 但在实际情况下, 给无人机用做航迹规划的时间是十分有限的, 因此, 如果能够用简单的方法, 快速的产生一个尽量靠近最优解的初始解, 则有希望能够使模拟退火算法在更短时间里得到一个更优的结果. 本文我们提出用简化的稀疏A*算法来产生模拟退火算法的初始解, 再将二者融合后得到的FSSA-SA算法用于最终的航迹规划. 具体实现时, 可将3.2.1节中模拟退火算法步骤(2)里的初始解产生方式换成由简化的稀疏A*算法得到.
稀疏A*算法[17]是一种启发式的搜索算法. 它的代价函数为
|
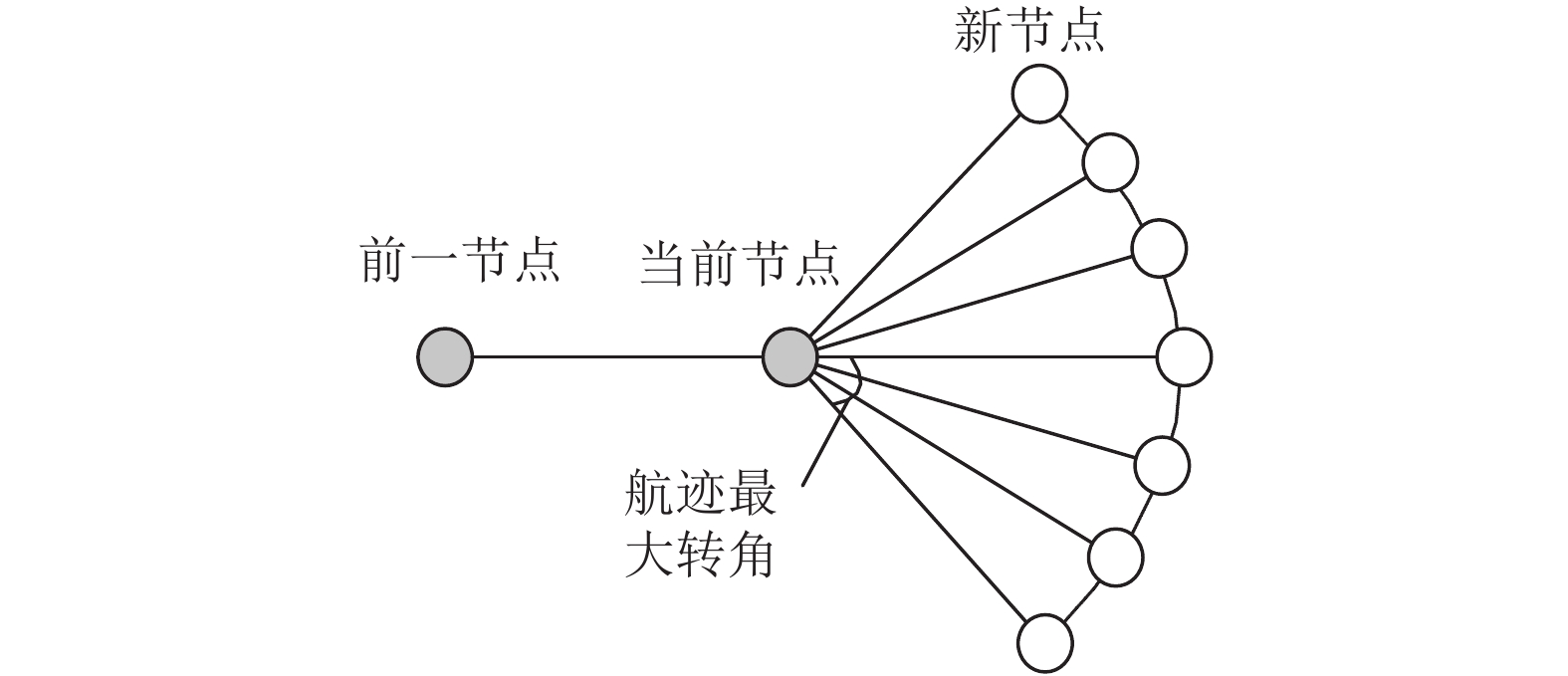
图 2 稀疏A*算法节点扩展示意图 |
算法在搜索航迹时, 从起始点开始向外逐步扩展产生备选节点. 如图2所示, 每次扩展都以一定步长, 按照当前前进的方向, 在满足无人机最大转向角约束的范围内, 产生新的节点. 再用这些新节点更新待扩展节点集, 并从所有待扩展节点中选择具有最小总代价估值f(n)的节点进行下一次的扩展. 我们借鉴文献[18]中提出的无记忆性思想, 对上述扩展过程进行简化: 每一次只从当前节点产生的待扩展节点中选择最优的一个进行下一步扩展. 通过这种简化, 我们可以快速的得到一个代价值相对较小的初始解. 简化后的稀疏A*算法的步骤为:
(1) 设置好搜索步长、相应角度参数、代价参数.
(2) 以起始点为当前点, 将终点的方向假定为此时前进的方向, 产生扩展节点.
(3) 分别计算各扩展节点对应的f(n). 选择具有最小f(n)值的节点作为新的当前点.
(4) 判断当前节点距离终点的距离是否小于等于一个步长, 若是, 则将终点加入航迹中, 算法结束. 否则转至步骤(5).
(5) 利用前一航迹节点和当前点以所确定的方向, 产生新的扩展节点, 转至步骤(3).
值得注意的是, 当面临的环境较为复杂时(比如存在近似"凹" 字形区域), 上述算法的这种"搜一步, 走一步" 的扩展模式, 很有可能会使搜索过程形成一个闭环. 换言之, 尚未扩展完成的航迹形成了闭合回路, 使得接下来的搜索过程在这条回路上周而复始, 陷入死循环. 为了避免上述情况的发生, 我们可以等角间距地产生新节点, 并使间距值不能整除360度.
通常情况下, 由于只是用来产生模拟退火算法的初始解, 所以对于简化的稀疏A*算法而言, 我们可以将航迹最大转角的值设置的更大一些, 从而能够更大范围的找寻每次扩展时的位置最优点. 但是假如环境中存在长时间无法跳出的搜索死区时, 则应适当缩小最大扩展角的范围(最极端情况下变为仅直线向前扩展), 以保证扩展的航迹能从组成搜索死区的威胁区中穿出, 继续向目标点扩展.
简化的稀疏A*算法由于每步只进行一次扩展, 所以对环境的感知能力是很有限的, 最终导致产生的航迹全局性较差. 为了改善这一点, 我们可以将原先的搜索起始点和终点调换一下, 再进行一次搜索, 然后将两条航迹进行对比, 选择具有较小综合代价的那条作为我们的规划初始航迹.

|
图 3 简化稀疏A*算法调换起始点前后的规划结果图 |
如图3中所示的规划情况中, 虚线表示的路径为利用简化稀疏A*算法从起始点向终点搜索得到的结果, 由于搜索过程中碰到了近似”凹” 形的威胁区域, 使得规划出的路径存在绕径. 而在调换起始点重新搜索后, 得出的图3中实线表示的路径则较优化的多, 更适合作为规划初始解.
3.2 对FSSA-SA算法中位置冗余节点的剔除退火过程中可能会出现两个或多个位置近似重合的节点, 这些节点在温度不高且所受扰动幅度较小的情况下显得多余: 既不能为改善航迹质量做出主要贡献, 又浪费了系统运行的时间. 对于这样的节点, 应该给与剔除, 以加快算法运行的速度. 产生位置相近似的冗余节点的主要原因如下:
第一, 退火过程中, 虽然节点的位置变化都是随机的, 但总航程会呈现出越来越小的趋势, 这就使得航迹节点的整体分布逐渐稠密化. 例如在图2中, C节点只有朝着接近A、B节点连线的方向上移动才能缩短航程, 进而它与A、B节点的距离变得更近了.
第二, 简化的稀疏A*算法在遇到较复杂环境时, 为了跳出"搜索死区", 会进行一定步数的搜索, 使得在当前扩展区域内的节点较为密集. 在后面的退火过程中, 为了减少被这些节点浪费掉的航程, 会使它们的位置变得更加紧凑.
剔除位置冗余节点的具体方法如下: 当系统温度下降至设定的低温段时, 对于每一个航迹中间节点, 不管其位置在受扰动后是否发生变化, 如果它与任何一个相邻航迹节点间的横纵坐标差值的绝对值都小于某一设定阈值, 则将其剔除.
4 仿真结果及分析我们将本文的FSSA-SA算法与稀疏A*算法[17]、模拟退火算法[16](后文简称SA算法)进行了仿真对比试验, 并对结果进行了分析. 实验中的规划环境大小为100km×100km, 威胁信息如表1所示(单位为km). 实验使用的PC系统为Windows7, 处理器型号为Intel(R) Core(TM)i7-6700, 主频率3.40 GHz.开发环境为Visual Studio, 编程语言为C++. 使用Matlab对规划环境和规划得到的航迹进行画图.
代价函数中, 威胁代价和油耗代价的权值系数a1, a2分别为20, 8, 油耗因子ωl为0.1. 算法的主要参数方面, 在稀疏A*及其简化算法中, 扩展步长为6; 模拟退火算法中, β0和β1的值分别为0.05和3.0, nsweeps的值在两次实验中依次为2000和1000, ds的初值为1.3, 并在退火过程的1/2和3/4以及9/10处分别减小至初值的0.8、0.5和0.3倍. FSSA-SA算法中, 在退火过程的后1/3段进行冗余节点剔除, 判断位置冗余的阈值设置为0.5.
| 表 1 威胁信息表 |
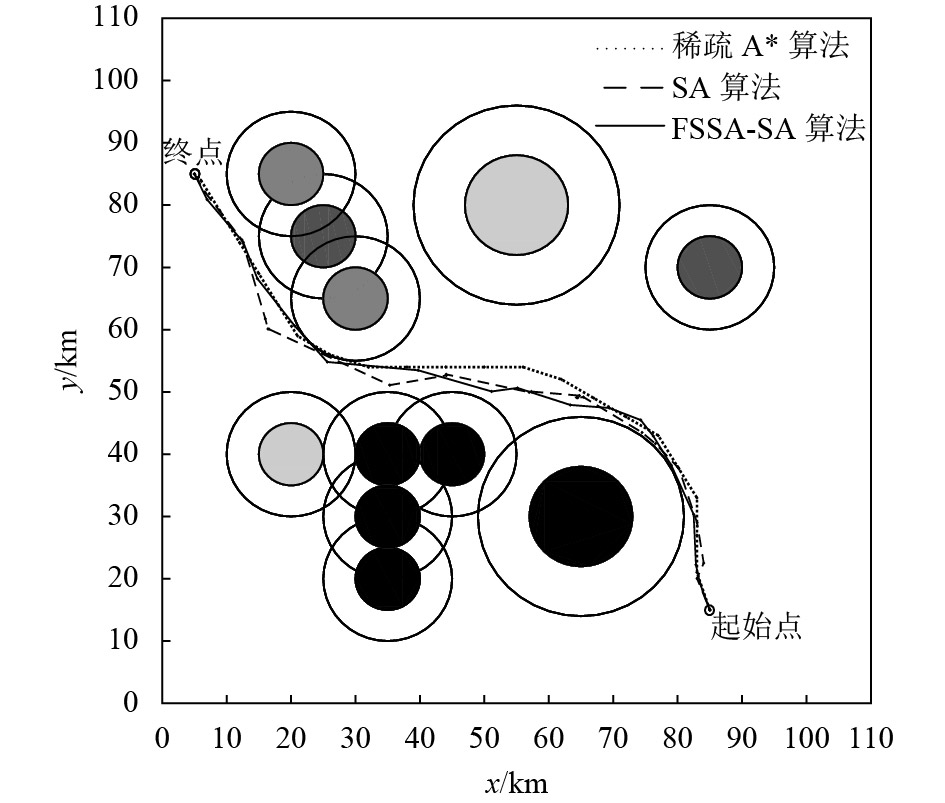
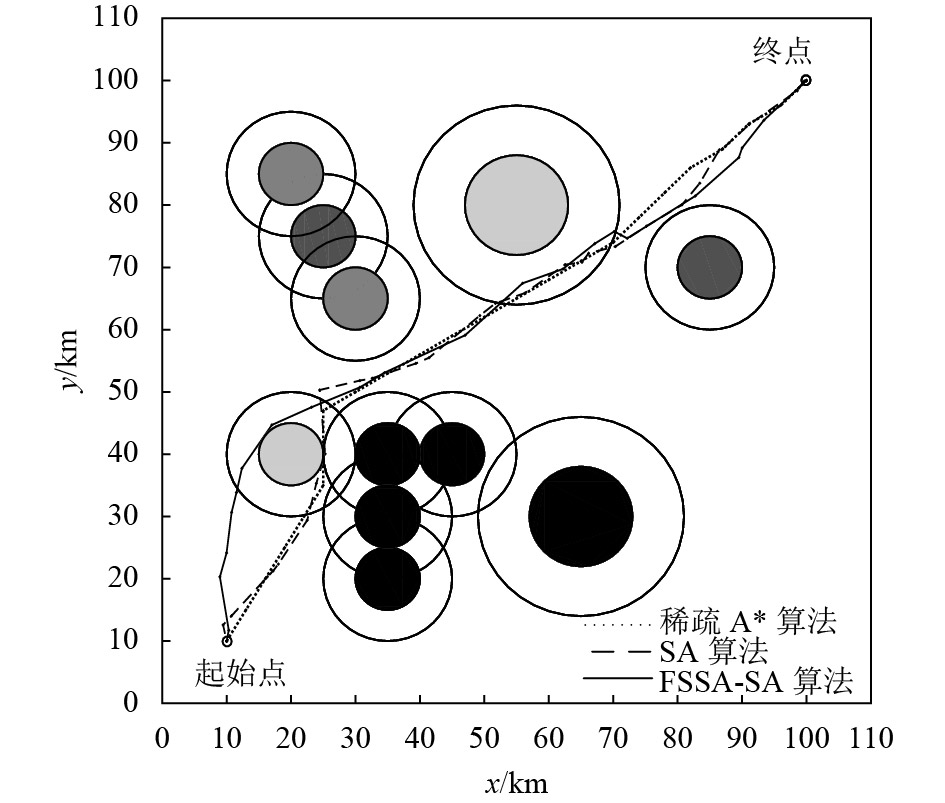
我们进行了两组规划仿真实验, 规划起止点分别为(85, 15)、(5, 85)和(10, 10)、(100, 100). 每组实验中, 每个算法都进行了10次航迹规划, 各自规划中最优结果见图4、5. 10次规划结果取均值后如表2所示.
从表2中的初始代价一项可以看出, 简化的稀疏A*算法相比于随机产生的方式能够得到更优化的初始航迹. 这是由于它在搜索初始航迹时, 在综合代价函数的作用下, 每一步都尽量选取威胁较小且尽量靠近目标点的节点作为下一个扩展节点. 换句话说, 算法的每一步的扩展都建立在对上一步扩展节点的择优选择之上, 这样能够尽量保证得到代价较低的初始航迹. 从表2中的最终代价均值可以看到, 从更优化的初始解开始再经过相同的退火过程之后, 新的FSSA-SA算法得出的结果要比SA算法更为优化.
忽略初始化的影响, 由SA与FSSA-SA算法的步骤可知, 它们在搜索航迹中的主要耗时取决于降温过程中, 对整条航迹反复遍历中的扰动与择优. 参数nsweeps的大小决定了反复遍历的次数, 航迹节点数目的大小决定了每次遍历中需要访问节点的个数. 对于SA算法而言, 其航迹节点数目始终恒定, 若设初始航迹节点数为m, 则
|
图 4 第一次仿真规划结果示意图 |
|
图 5 第二次仿真规划结果示意图 |
从表2可知, 相比于稀疏A*算法的搜索结果, 虽然FSSA-SA算法最终航迹代价略高, 但其占用了较少的节点内存空间, 花费了较少的搜索时间. 稀疏A*算法的内存占用量与运行耗时会随着搜索覆盖范围的增大而增加, 因为其要遍历每一个已到访位置和为它们提供储存空间. FSSA-SA算法的耗时前文已做出分析, 它的运行内存占用量主要由简化稀疏A*算法决定. 简化的稀疏A*算法在搜索过程中, 一方面保存已搜得的路径节点, 另一方面只保存被扩展节点的当前最优子节点, 所以在搜得整条初始航迹时的耗存节点数最大. 在后续的退火过程中, 由于去冗余节点操作的存在, 这些节点的数目只可能减少而不会增加. 因此, FSSA-SA算法的最大耗存节点数取决于简化稀疏A*算法规划出的初始解节点数大小.
| 表 2 规划结果对比表 |
观察图4、5可以看到, FSSA-SA算法规划的航迹整体较为平滑. 这是因为: 为了缩短航程, 文中设计的新解产生方式能够使得航迹上的每一个中间节点, 都尽量的与它相邻的两个节点构成一条直线. 进而从整体看来, 航迹中没有较大的转角出现, 更适合无人机实际的飞行.
5 结束语本文为解决威胁环境下的无人机航迹规划问题, 提出了一种FSSA-SA算法. 该算法中, 使用简化稀疏A*算法为模拟退火算法产生初始解, 并通过将某一节点在与其两个相邻节点连线垂直的方向上进行随机移动, 实现对退火过程中随机扰动的模拟, 在低温区时, 对于位置冗余的节点进行了剔除. 实验结果表明, 本文FSSA-SA算法能够利用较少内存, 快速的得到一条综合代价较低且较为平滑的航迹, 在实时性要求较高并且存储资源有限的规划情况下, 具有一定的实用性.
| [1] |
Liu LF, Shi RX, Li SD, et al. Path planning for UAVS based on improved artificial potential field method through changing the repulsive potential function. Proceedings of 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC). Nanjing, China. 2016. 2011–2015.
|
| [2] |
胡中华, 赵敏, 姚敏, 等. 无人机航迹规划技术研究及发展趋势. 航空电子技术, 2009, 40(2): 24-29, 36. DOI:10.3969/j.issn.1006-141X.2009.02.006 |
| [3] |
Qi Z, Shao ZH, Ping YS, et al. An improved heuristic algorithm for UAV path planning in 3D environment. Proceedings of the Second International Conference on Intelligent Human-Machine Systems and Cybernetics. Nanjing, China. 2010. 258–261.
|
| [4] |
Li H, Fu Y, Elgazzar K, et al. Path planning for multiple Unmanned Aerial Vehicles using genetic algorithms. Proceedings of 2009 Canadian Conference on Electrical and Computer Engineering. St. John’s, NL, Canada. 2009. 1129–1132.
|
| [5] |
白俊强, 柳长安. 基于蚁群算法的无人机航路规划. 飞行力学, 2005, 23(2): 9-12. |
| [6] |
Lin MX, Yuan K, Shi CZ, et al. Path planning of mobile robot based on improved A* algorithm. Proceedings of the 29th Chinese Control and Decision Conference. Chongqing, China. 2017. 3570–3576.
|
| [7] |
王维, 裴东, 冯璋. 改进A*算法的移动机器人最短路径规划
. 计算机应用, 2018, 38(5): 1523-1526. |
| [8] |
姚雨, 李庆, 陈曦. 优化的A*算法在航迹规划上的应用
. 微电子学与计算机, 2017, 34(7): 51-55. |
| [9] |
何平川, 戴树岭. 一种改进的UAV三维航迹实时规划算法. 北京航空航天大学学报, 2010, 36(10): 1248-1251. |
| [10] |
王雷, 李明, 蔡劲草, 等. 改进遗传算法在移动机器人路径规划中的应用研究. 机械科学与技术, 2017, 36(5): 711-716. |
| [11] |
赖智铭, 郭躬德. 基于自适应阈值蚁群算法的路径规划算法. 计算机系统应用, 2014, 23(2): 113-118, 59. DOI:10.3969/j.issn.1003-3254.2014.02.019 |
| [12] |
Aarts E, Korst J. Simulated Annealing and Boltzmann Machines. Chichester: Wiley, 1989.
|
| [13] |
胡中华. 基于智能优化算法的无人机航迹规划若干关键技术研究[博士学位论文]. 南京: 南京航空航天大学, 2011.
|
| [14] |
赵毓. 基于群体智能算法的无人机航迹规划研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [15] |
Kirkpatrick S, Gelatt CD Jr, Vecchi MP. Optimization by simulated annealing. Science, 1983, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
| [16] |
耿修堂, 吴勇, 许进. 基于禁忌退火算法的巡航导弹航迹规划. 火力与指挥控制, 2009, 34(11): 43-47. DOI:10.3969/j.issn.1002-0640.2009.11.012 |
| [17] |
Szczerba RJ, Galkowski P, Glicktein IS, et al. Robust algorithm for real-time route planning. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(3): 869-878. DOI:10.1109/7.869506 |
| [18] |
何雨枫, 曾庆化, 王云舒, 等. 室内微型飞行器实时路径规划算法研究. 电子测量技术, 2014, 37(2): 23-27. DOI:10.3969/j.issn.1002-8978.2014.02.007 |
 2019, Vol. 28
2019, Vol. 28


