智能制造正被吹捧为下一次工业革命. 利用统计知识结合大数据机器学习算法预测产品故障率, 以提高生产力并保持竞争力, 俨然成为下一步制造业企业争相追逐的目标. 针对制造业的生产流水线数据, 建立一个故障检测模型, 有利于企业及时发现产品生产过程中的问题并对其修正, 从而实现更精细的智能制造过程. 目前国内外学者提出的针对大数据的预测方法主要包括神经网络预测法[1,2]、基于降维手段的传统机器学习预测法[3–6]. 神经网络法虽然有很高的精度, 但往往算法时间成本高, 可解释性不强, 同时传统的机器学习算法对于大规模数据集在节约内存和时间开销方面也往往不尽如人意. 针对以上问题, 学者们提出了相应的改进方法. 文献[7]提出了一种具有动态结构的RBF神经网络, 文中方法通过基于神经元活动性和互信息来在线添加或删除神经网络隐含层神经元, 以实现平衡网络的复杂性和整体计算效率. 文献[8]针对工业系统数据的预测问题, 提出了一种能够并行的基于共享储备池模块化的神经网络预测模型. 该方法采用K均值聚类方法将样本数据分类并分别建模, 在建模过程中提出一种改进的回声状态网络, 通过对神经网络进行模块化处理能够将问题求解空间分层, 相比单一神经网络具有更好的泛化性能. 文献[9]在对风机运行状态数据划分不同时间窗的基础上, 运用LightGBM、XGBoost、ERT模型进行嵌套融合, 得到混合模型, 缩小可疑故障数据的范围, 保证较为准确的情况下基本覆盖到几乎全部的故障数据, 并在再次细分的时间窗下得到更好的效果. 上述改进方法存在的一个共性问题是, 真实工业环境下, 生产数据在流水线上几乎以秒为单位不断产出, 因此预测模型需要不断迭代以适应新的生产状况, 上述方法虽然相比传统方法在模型的计算效率和准确率有了很大提升, 但在面对真实工业数据时, 模型的迭代速度仍然不能满足企业需求.针对该问题, 本文提出了一种基于FTRL[10]和XGBoost[11]算法的产品故障预测模型, 可以在保证预测准确率同时, 加速模型的迭代速度, 本文将其应用于真实的制造业数据, 取得了令人满意的效果.
2 数据来源与分析 2.1 数据来源本文使用的数据来自德国的工业企业博世公司发布的一份规模庞大(14.3 GB)的匿名数据集, 这份数据集由百万条生产流水线记录组成, 每条记录都测量了产品在生产流水线不同部分的相关信息, 博世公司希望各界学者挑战预测产品故障这一难题, 从而使博世能够以最低的成本为最终用户带来优质的产品. 该数据集包含三种类型的特征: 数值型特征968个, 分类型特征2140个, 时间序列特征1156个以及预测标签. 其中训练数据含有1184 687个样本(其中包括1176 868个正样本, 6879个负样本), 用于衡量模型性能的测试数据含有1182 748个样本. 针对如此庞大规模的数据集, 如何才能将其有效利用并建立预测模型, 确实是一个不小的挑战.
2.2 数据分析数值型特征的命名方式包含了与生产记录有关的工作站, 生产线和测量值信息. 例如, 生产记录名L3_S50_F4243的特征表示某部件的生产流程通过生为产线3, 工作站50(每个工作站所属的生产线唯一), 并且特征值对应的测量方式编号为4243. 为了直观了解工厂的运作方式, 笔者利用数值特征, 构造了如图1所示的工厂生产流水线框架图(数字代表对应的工作站台), 其中共含有8197条唯一的生产路径.

|
图 1 工厂生产流水线框架 |
通常来讲, 相似的产品类型在不同的生产线上往往具有相近的生产时间, 为了有效区分不同类型的产品, 本文手动构建了一类时间差特征, 来衡量产品在每条生产线上的流通时间, 下文将这类特征统一称作time_diff特征.
原始数据集除去空值特征后类别型特征共有1990个. 针对分类型特征, 一个经典的处理方式是通过one-hot编码. 由于数据集的分类型特征本身数量就非常多, 再进行one-hot编码处理会使得特征量爆炸式增长, 加上数据集的样本量又非常大, 这就使得传统的机器学习算法很难再针对所有特征去拟合一个学习模型. 因此下文笔者会针对该问题提出相应的解决办法.
时间序列特征名称由生产线、站台、日期三部分组成. 例如, 对于时间序列特征L3_S50_D4242, 其表明当产品通过生产线3, 工作站台50, 并且数值特征(或分类特征)的测量方式id为4241时所发生的具体时间. 为了弄清楚时间序列值的具体含义, 笔者将时间滞后差作为x轴, 对应的自相关系数作为y轴, 建立如图2所示的关系图. 我们可以发现时间序列特征一个周期的区间跨度为16.75, 每个周期存在7个局部峰值, 据此笔者推断一个周期为一个星期. 也就是说, 1周对应的时间序列特征值为16.75, 至少每六分钟(0.01)生成一个产品记录. 因此原始数据集记录了102.6周(约两年多)的生产记录.

|
图 2 不同滞后区间下的自相关系数 |
2.3 解决方案思路
总结该数据集, 其具有样本量大, 特征量大且类型多样,时间跨度大, 正负样本不平衡的特点, 并且数据集的样本以流的形式不断获取. 笔者从以下角度出发, 最终决定采用本文的故障预测框架: 首先, 由于数据样本量和特征量都很庞大, 这就要求模型的数量尽可能少而精, 其次, 样本中分类特征与传统工业数据相比, 量级显然多很多, 为了兼顾计算效率和模型的性能, 本文创造性将其类比为一个点击率预估的建模问题, 采取典型的FTRL点击率预估模型来对待分类特征, 最终, 进一步地, 本文在建模时没有采取传统的模型融合策略, 而是利用FTRL模型将分类特征转化为一列特征放进XGBoost中训练, 这么做既通过降低建模的复杂度来保证了模型的迭代速度, 又间接利用了模型融合的思想, 保证了模型的精确度.
3 模型理论基础 3.1 FTRL (Follow the Regularized Leader)理论基础一直以来, 利用在线学习(Online learning)[12]算法优化的广义线性模型(Logistic Regression, LR)被广泛应用于大规模机器学习问题中. 在线学习算法以数据流的形式从硬盘中读取文件, 每个训练样本只需考虑一次, 即通过在线梯度下降(Online Gradient Descent, OGD)的方法来优化损失函数, 这种方法能够高效地训练大数据集. OGD算法在实践中已被证明能够有效地解决大规模机器学习问题, 其能够在最小化所耗计算资源的同时提供不错的预测精度. 然而OGD算法对于产生稀疏模型并不太尽如人意. 模型的稀疏化指的是实践过程中我们希望通过减少权重向量的非零解来去除冗余变量, 只保留与预测变量最相关的解释变量. 实现该目的往往通过向目标损失函数中加入L1范数, 这里L1范数是指特征权重向量中各个元素的绝对值之和, 它在零处不可微, 因此当最小化损失函数后得到的最优解会使权重向量的大部分元素变为零, 剩下的较大的权重向量值对应的特征往往是与目标向量最相关的特征. 从本文的故障预测角度来看, 虽然特征有近千维, 但能够持续稳定预测故障是否发生的特征通常不过几百维度, 其他特征往往是导致当下发生故障的随机因素, 当面对未来发生的故障时不起任何预警作用, 引入L1范数能够学习地去掉这些没有信息的特征, 也就是把这些特征对应的权重置为零. 因此这种方法能够有效降低模型复杂度, 提高泛化性, 同时也保留了与目标变量最相关的解释变量.
3.2 FTRL优化算法介绍FTRL最初由Google的H.Brendan McMahan于2010年提出, 近年来国内外各大企业将其应用于自身行业的相关业务, 都取得了很好的效果. FTRL与以往在线算法不同, 其对特征权重每一维分量采取不同的更新方式, 假设给定损失函数对特征权重第i维的梯度向量为
| $ \begin{array}{l} w_i^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm {if}}|z{i^{(t)}}| < \lambda _1}\\ { - {{\left({\lambda _2} + \displaystyle\sum\limits_{s = 1}^t {{\sigma ^{(s)}}} \right)}^{ - 1}}\left(z_i^{(t)} - {\lambda _1}{\mathop{\rm sgn}} (z_i^{(t)})\right)\;\;\;{\rm {otherwise}}} \end{array}} \right.\\ {\rm {where}}\displaystyle\sum\limits_{s = 1}^t {{\sigma ^{(s)}}} = {\textstyle{1 \over {{\eta _i}}}},\eta _i = \dfrac{\alpha }{{\beta + \sqrt {\displaystyle\sum\nolimits_{s = 1}^t {g_{s,i}^2} } }} \end{array} $ |
其中,
由于本文采用的数据集是在制造业企业的生产线上以流形式不断获取的, 而one-hot编码后的类别特征又非常稀疏,因此对其建立FTRL-LR模型.
3.3 XGBoost算法相关理论基础XGBoost全称为eXtreme Gradient Boosting, 是GBDT (Gradient BoostingDecision Tree)算法的一种, 顾名思义, 其思想主要由两部分组成: Decison Tree[13](决策树)算法和Gradient Boosting[14](梯度提升)算法.
XGBoost计算效率高, 泛化能力强, 并且可以大大降低人工特征工程的工作量, 因此将其作为最终的预测模型. XGBoost相对于GBDT的算法步骤, 主要的改变是对损失函数生成二阶泰勒展开,并在代价函数里加入了正则项, 用于控制模型的复杂度. 正则项里包含了树的叶子节点个数、每个叶子节点上输出的权重得分的平方和. 从平衡偏差方差的角度来讲, 正则项降低了模型的方差, 使学习出来的模型更加简单和稳健, 防止过拟合, 这是XGBoost优于传统GBDT的特性之一. 在工程实现方面, XGBoost工具支持并行, 其并行不是树粒度层面上的,而是在特征粒度层面上的. 众所周知, 决策树学习最耗时的一个步骤就是根据特征的值对训练样本进行排序以确定最佳分割点, 而XGBoost在训练之前, 预先对数据进行了排序,然后保存为block(块)结构, 后面的迭代中重复地使用这个结构, 大大减小了计算量. 这个block结构也使得并行成为了可能, 在进行节点的分裂时, 需要计算每个特征的增益,即用贪心法枚举所有可能的分割点, 最终选增益最大的那个特征去做分裂, 那么各个特征的增益计算就可以开多线程进行. XGBoost算法的主要步骤为:
(1) 构造目标损失函数:
| $ \begin{array}{l} L(\varphi ) = \displaystyle\sum\limits_i {l(\hat y_i} ,y_i) + \sum\limits_k {\Omega (f_k)} ,\\ \Omega (f) = \gamma T + {\textstyle{1 \over 2}}\lambda ||w|{|^2} \end{array} $ |
XGBoost在目标函数中加上了正则化项, 基学器为CART(决策树的一种)时, 正则化项与树的叶子节点的数量T以及叶子节点的值有关.
(2) 训练目标函数, 将第t次的loss二次泰勒展开并掉常数项.
| $ \begin{array}{l} {L^{(t)}} = \displaystyle\sum\limits_{i = 1}^n {l(y_i} ,\hat y{_i^{(t - 1)}} + f_t(x_i)) + \Omega (f_t)\\ {L^{(t)}} \approx \displaystyle\sum\limits_{i = 1}^n {[l(y_i} ,\hat y{_i^{(t - 1)}}) + {g_i}f_t(x_i) + {\textstyle{1 \over 2}}{h_i}f{_t^2}(x_i)] + \Omega (f_t)\\ {\rm {where}}\left( {{g_i} = {\partial _{\hat y{_i^{(t - 1)}}}}l(y_i,\hat y{_i^{(t - 1)}}),{h_i} = {\partial ^2}_{\hat y{_i^{(t - 1)}}}l(y_i,\hat y{i^{(t - 1)}})} \right)\\ {{\bar L}^{(t)}} \approx \displaystyle\sum\limits_{i = 1}^n [ {g_i}f_t(x_i) + {\textstyle{1 \over 2}}{h_i}f{_t^2}(x_i)] + \Omega (f_t) \end{array} $ |
(3) 求出目标函数最优解:
| $ {L^{(t)}}(q) = - \dfrac{1}{2}\displaystyle\sum\limits_{j = 1}^T {\dfrac{{{{(\sum\limits_{i \in g_i} {g_i} )}^2}}}{{\displaystyle\sum\limits_{i \in I_j} {h_i + \lambda } }}} + \gamma T $ |
本文采用的是XGBoost的Python版本, 其中重点关注的几个超参数包括:
(1) Learning_rate: 学习率. 设置地相对小些可以让模型学的更加精确.
(2) n_estimators: 提升阶段树的最大迭代轮数. 这一参数和往往和学习率一起结合early_stopping_rouds参数使用, 用来防止过拟合.
(3) early_stopping_rounds: 当模型在指定验证集上的表现不再提升时, 停止迭代.
(4) max_depth: 每颗决策树的最大深度. 这一参数限制了树中的最多节点数. 值越小模型越保守.
(5) nthreads: 并行训练的最大进程数. –1代表无限制.
(6) min_child_weight: 进一步分裂一个子节点的最小Hessian和.
4 实验过程 4.1 建模框架针对前文数据分析过程中提到的问题, 为了保证模型预测性能良好的同时又兼顾模型迭代速度和节约内存, 笔者决定采用分而治之的思想, 对类别特征建立利用FTRL算法优化的Logistic Regression模型(以下简称FTRL-LR), 并利用out-fold prediction (stacking方法的本质思想)[15]方法生成新特征. 如此做的合理性有二, 一是减少冗余的同时最大化分类特征信息, out-fod prediction生成的特征其实是一种滞后特征, 它从分类特征中的学到最有用的信息并以单个特征储存起来, 可以去除特征中的随机噪声, 提高了模型的鲁棒性, 二是间接达到模型集成的效果, 如果将原始所有分类特征用XGBoost训练, 那么不仅增加了模型的复杂度, 而且也没有利用到模型集成的优势, 也就是会忽略FTRL模型学习到的信息.
接下来将该特征和数值特征, 时间序列特征以及人工特征一起建立XGBoost模型. 利用XGBoost算法建立预测模型包含两个阶段. 第一个阶段是特征选择阶段, 当XGBoost建模完成后, 会返回一个特征重要性结果. XGBoost通过统计特征在每棵决策树中被用来划分数据的次数, 并用每次划分所带来的训练损失减益来对特征划分次数进行加权求和, 最后再对所有树求平均得到特征重要性. 针对除类别特征外的所有特征(包括手工构建的time_diff类特征)利用XGBoost进行特征选择, 选取特征重要性TOP200的特征, 再和之前通过类别特征得到的一列数值特征一起作为最终XGBoost的建模特征.
对于模型的超参数选择, 本文采取贝叶斯最优化来获得. 贝叶斯优化用于机器学习调参由Snoek[16]提出, 其主要思想是, 给定优化的目标函数(本文优化的目标函数为训练集三折交叉验证的MCC得分), 通过不断地添加样本点来更新目标函数的后验分布(高斯过程), 直到后验分布基本贴合于真实分布. 这种方法的优势包括由于其采用高斯过程, 考虑之前的参数信息, 不断地更新先验, 这使得参迭选择的代次数少, 速度快, 而且贝叶斯调参针对非凸问题依然稳健, 不容易陷入局部最优.
最终对于FTRL-RL模型, 超参数设置分别为α=0.3284, β=0.6725, L1=5.698, L2=0.2587. 对于预测阶段的XGBoost模型超参数设置分别为learning_rate=0.05, max_depth=6, min_child_weight=1, n_estimators=1000, nthread=–1, early_stopping_rounds=50.
4.2 评价指标MCC (Matthews Correlation Coefficient)[17]即马修斯相关系数通常作为二分类问题的一个评价指标. 二分类问题的预测结果中包含四种类型的样本, 分别是被模型分类正确的正样本、被模型分类错误的正样本、被模型分类错误的负样本和被模型分类正确的负样本, 分别表示为TP、FN、FP和TN. MCC指标的计算公式为:
| $ MCC = \frac{{TP \times TN - FP \times FN}}{{\sqrt {(TP + FP)(TP + FN)(TN + FP)(TN + FN)} }} $ |
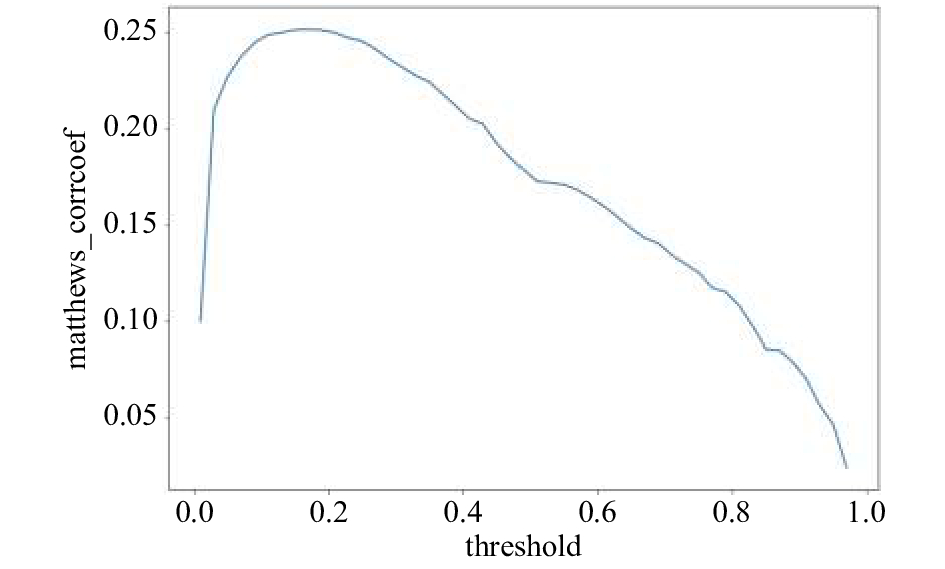
该指标综合考虑了真阳性、真阴性和假阳性和假阴性,是一个比较均衡的指标, 即使是在正负样本量差别很大时,也能起到很好的衡量效果. 由于本实验的数据集正负样本很不平衡, 因此选用MCC作为我们的评价指标. 由于最终预测模型的输出结果为概率形式(产品发生故障的概率), 因此为了得到最优MCC值对应的分类概率阈值, 笔者通过计算不同阈值下训练集的三折交叉验证MCC得分, 作出如图3的关系曲线. 我们可以发现最优阈值0.2(比正常阈值选择0.5低很多), 对应的训练集三折交叉验证MCC得分为0.25.
|
图 3 不同阈值下训练集的三折交叉验证MCC得分 |
4.3 实验结果
本文的所有实验(特征可视化, 模型建立与衡量)都是在谷歌云实例上运行, 其环境配置为Ubuntu 16.04, 8个vCPU, 52 GB内存, 编程语言为Python. 若需实验代码,可向笔者索取.
表1为不同学习框架效果对比. 通过对比可以发现 FTRL和XGBoost相结合的预测框架预测效果最好. 同时该预测框架也具有较好的可解释性, 最终XGBoost预测模型得出的重要特征包括生产线末期阶段的一些特征, 区分不同产品类型的时间差特征, 由类别特征得到的数值特征. 根据以上结果笔者推断, 不同的产品类型往往具有不同的故障发生率, 一些需要更复杂的制造阶段, 生产更耗时的产品也通常更容易发生故障.
| 表 1 不同学习框架效果对比 |
5 结论与展望
大数据时代, 制造业已经进入了生产智能化的发展阶段,充分利用生产流水线上输出的大数据加速这一进程变得至关重要. 本文将FTRL-LR模型和XGBoost模型结合起来, 充分利用各自的优势, 建立了一个产品故障预测模型. 实验结果表明, 此模型相比传统的预测模型, 具有预测精度高, 泛化能力强, 计算效率高, 内存耗用低, 可解释性强的优势. 基于该模型, 制造业可以提前预测产品生产过程中可能发生的故障, 并对其及时进行修正. 这种方法可以有效降低企业的生产成本和时间成本, 实现更智能化的工厂作业流程. 进一步地, 由于原始数据集涉及大量不同类型的产品生产, 因此笔者发现还可以利用层次聚类的方法对不同的产品类型分别建模(在保障时间成本的前提下), 实现更精细化的预测框架, 所以未来本文的方法还有很大的提升空间.
| [1] |
刘崇, 祝锡永. 基于BP神经网络的医保欺诈识别. 计算机系统应用, 2018, 27(6): 34-39. DOI:10.15888/j.cnki.csa.006363 |
| [2] |
Li B, Chow MY, Tipsuwan Y, et al. Neural-network-based motor rolling bearing fault diagnosis. IEEE Transactions on Industrial Electronics, 2002, 47(5): 1060-1069. |
| [3] |
宋鹏, 胡永宏. 基于矩阵值因子模型的高维已实现协方差矩阵建模. 统计研究, 2017, 34(11): 109-117. |
| [4] |
刘俊, 王旭, 郝旭东, 等. 基于多维气象数据和PCA-BP神经网络的光伏发电功率预测. 电网与清洁能源, 2017, 33(1): 122-129. DOI:10.3969/j.issn.1674-3814.2017.01.019 |
| [5] |
宋乐见, 张晓龙, 陈同兴, 等. 基于KPCA与PSO-WLSSVM的顶吹熔炼系统喷枪寿命预测研究. 计算机与应用化学, 2017, 34(1): 59-63. |
| [6] |
Fong SM, Wong R, Vasilakos AV. Accelerated PSO swarm search feature selection for data stream mining big data. IEEE Transactions on Services Computing, 2016, 9(1): 33-45. |
| [7] |
Han HG, Chen QL, Qiao JF. An efficient self-organizing RBF neural network for water quality prediction. Neural Networks, 2011, 24(7): 717-725. DOI:10.1016/j.neunet.2011.04.006 |
| [8] |
车艳军. 模块化神经网络及其并行算法的工业系统预测[硕士学位论文]. 大连: 大连理工大学, 2016.
|
| [9] |
张丹峰. 基于LightGBM, XGBoost, ERT混合模型的风机叶片结冰预测研究[硕士学位论文]. 上海: 上海师范大学, 2018.
|
| [10] |
McMahan HB. Follow-the-regularized-leader and mirror descent: Equivalence theorems and L1 Regularization. Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, FL, USA. 2011. 525–533.
|
| [11] |
Chen TQ, Guestrin C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, CA, USA. 2016. 785–794.
|
| [12] |
李志杰, 李元香, 王峰, 等. 面向大数据分析的在线学习算法综述. 计算机研究与发展, 2015, 52(8): 1707-1721. |
| [13] |
冯少荣. 决策树算法的研究与改进. 厦门大学学报(自然科学版), 2007, 46(4): 496-500. DOI:10.3321/j.issn:0438-0479.2007.04.013 |
| [14] |
Friedman JH. Greedy function approximation: A gradient boosting machine. The Annals of Statistics, 2001, 29(5): 1189-1232. |
| [15] |
周志华. 通过集成学习进行知识获取. 重庆邮电大学学报(自然科学版), 2008, 20(3): 361-362. |
| [16] |
Snoek J, Larochelle H, Adams RP. Practical Bayesian optimization of machine learning algorithms. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, NV, USA. 2012. 2951–2959.
|
| [17] |
Jurman G, Riccadonna S, Furlanello C. A comparison of MCC and CEN error measures in multi-class prediction. PLoS One, 2012, 7(8): e41882. DOI:10.1371/journal.pone.0041882 |
 2019, Vol. 28
2019, Vol. 28


