互联网的快速发展给人们的生活带来了极大的便利, 同时, 海量的信息数据引发了“信息超载”问题[1]. 个性化推荐系统应运而生, 通过对用户兴趣建模, 在海量的数据中找到合适的物品推荐给用户, 极大地提高了信息使用率[2].
推荐系统常用的推荐算法有: 基于内容的推荐、基于关联规则的推荐、基于知识的推荐以及协同过滤推荐[3–5]. 其中, 协同过滤推荐算法是应用最成功最广泛的一种算法.
协同过滤算法依然面临着诸多局限性, 包括数据稀疏性、冷启动、可扩展等问题, 影响了系统的推荐结果和推荐质量.
1 传统的协同过滤算法根据用户行为数据设计的算法称为协同过滤算法[6]. 协同过滤算法建立在数据挖掘的基础上, 算法的工作原理是: 根据用户的历史评分计算相似度, 相似度高的判为目标用户的邻居用户, 依据邻居集用户的历史评分计算目标用户的可能评分值, 将评分值高的前N项推荐给目标用户(Top-N推荐).
协同过滤算法可以分为基于用户的协同过滤(user-based CF)和基于项目的协同过滤(item-based CF).
1.1 冷启动问题协同过滤的冷启动问题分为新用户冷启动、新项目冷启动和新系统冷启动, 协同过滤算法的核心是分析用户-项目评分矩阵, 计算相似度. 当系统中有新用户加入时, 该用户在系统中不存在历史评分数据, 不能根据传统算法计算用户间的相似度, 也就无法为其进行推荐, 这就是协同过滤算法的新用户冷启动问题[7]; 同样地, 当系统中加入新项目时, 由于没有该项目的历史评分记录, 推荐算法难以将该项目推荐给用户, 这就是新项目的冷启动问题.
1.2 冷启动问题的研究现状近年来, 许多专家学者对冷启动问题提出了一系列的解决办法, 比如众数法、平均值法、相似度度量法等等[8], 减少了冷启动问题对推荐质量的影响.
Xu JW, Yao Y等提出了一种新型的评分比较策略(RaPare)[9]学习冷启动用户/项目的潜在性能, 通过寻找冷启动用户/项目和现有用户/项目之间的差异, 为冷启动用户/项目的潜在性能提供细粒度校准. Nguyen VD, Sriboonchitta S, Huynh VN引入了一种用户社交网络和软评分相结合的协同过滤推荐系统[10], 通过用户社交网络提取社区特征来解决冷启动问题. Katarya R, Verma OP将计算相似性的不对称方法与矩阵分解和基于典型性的协同过滤(Tyco)相结合[11], 实现了一种改进的电影推荐算法. 改进算法采用了Pearson相关系数计算相似度, 用线性回归进行预测, 得到更好的推荐结果.
2 相似度的计算方法 2.1 传统的相似度算法协同过滤算法根据相似度的计算结果找到目标用户/项目的邻居集, 因此相似度的计算方法很重要, 目前常见的相似度计算方法有: 余弦相似度、欧几里德距离和Pearson相关系数等等.
余弦相似度:
| $ sim(u,j) = \frac{{\displaystyle\sum\limits_{i = 1}^n {{u_i} \cdot {j_i}} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{\left( {{u_i}} \right)}^2}} } \cdot \sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({j_i})}^2}} } }} $ | (1) |
欧几里德距离:
| ${{d}}\left( {u,j} \right) = \sqrt {\sum {{{\left( {{u_i} - {j_i}} \right)}^2}} } $ | (2) |
| ${{sim}}\left( {u,j} \right) = \frac{1}{{1 + d\left( {u,j} \right)}}$ | (3) |
Pearson相关系数:
| $sim\left( {u,j} \right) = \frac{{\displaystyle\sum\limits_{i \in {I_{u,j}}}^n {\left( {{R_{u,i}} - \overline {{R_u}} } \right)} \left( {{R_{j,i}} - \overline {{R_j}} } \right)}}{{\sqrt {\displaystyle\sum\limits_{i \in {I_{u,j}}}^n {{{\left( {{R_{u,i}} - \overline {{R_u}} } \right)}^2}} } \sqrt {\displaystyle\sum\limits_{i \in {I_{u,j}}}^n {{{\left( {{R_{j,i}} - \overline {{R_j}} } \right)}^2}} } }}$ | (4) |
其中,
通常, 各推荐网站的数据库中会含有关于用户属性信息的数据集, 常见的用户属性包括: 用户ID,性别, 年龄, 职业, 个人偏好等等. 某些网站在用户注册时会询问其可能喜欢的类型, 以此达到更优的推荐效果. 具有相同或者相近属性的两个用户会表现出更相近的兴趣爱好[12]. 因此, 本文以用户的个人信息属性为切入点, 为了解决新用户的冷启动问题, 通过分析用户的基本信息特征, 设计了一种融合用户信息模型的基于用户的协同过滤算法.
新算法综合考虑了用户的k项基本信息值
| $attr(u,v) = \sum\limits_{i = 1}^k {{\lambda _i} \cdot att{r_i}} $ | (5) |
其中,
| $\sum\limits_{i = 1}^k {{\lambda _{{i}}}} = 1$ | (6) |
求得用户特征差值
| $s(x) = \frac{1}{{1 + {e^{ - x}}}}$ | (7) |
| $si{m_{attr}}\left( {u,v} \right) = 2 \times (1 - \frac{1}{{1 + \exp ( - attr(u,v))}})$ | (8) |
当用户间相同特征较多时, 量化后的特征差值较小,
| ${p_{i,j}} = \overline {{p_i}} + \frac{{\sum\nolimits_{u \in C} {sim({u_i},{u_j}) \times ({R_{u,i}} - \overline {{R_u}} )} }}{{\sum\nolimits_{u \in C} {\left| {sim({u_i},{u_j})} \right|} }}$ | (9) |
融合用户信息模型的基于用户的协同过滤算法流程图如图1所示.

|
图 1 新用户冷启动算法 |
2.2.2 采用层次聚类的基于项目的协同过滤算法
协同过滤冷启动问题的另一方面是新项目的冷启动. 推荐系统中的项目都有各自的内容信息, 比如书籍的书名、出版年份、类型、作者; 食品的类别、成分; 音乐的年份、流派、作曲者等等. 在没有项目历史评分记录数据的情况下, 本文的新算法根据这些内容信息, 分析物品内容之间的相关度获取新项目和其他项目之间的相似度, 提出了采用凝聚式层次聚类的新项目相似度算法.
凝聚式层次聚类的相似度计算主要分为三步进行:
(1) 数据初始化处理
对于数值类信息, 可直接用于欧式距离计算. 对非数值类信息, 计算项目属性信息的补集元素个数, 作为欧氏距离中某一维上的距离长度值.
比如书本A的出版年份是2015年, 类别标签有: 数据分析/Python编程/深度学习, 出版社是人民邮电出版社; 书本B的出版年份是2018年, 类别标签有: 数据分析/Matlab编程/深度学习, 出版社是人民邮电出版社. 那么, A1–B1=3, A2–B2=1, A3–B3=0. 这三个值用于计算A, B之间的欧式距离.
(2) 计算欧式距离
假设项目有n种内容信息, 项目i对应的第k种内容信息记为
| ${{d}}\left( {{{i}},j} \right) = \sqrt {\sum\limits_{k = 1}^n {{{({{{i}}_k} - {j_k})}^2}} } $ | (10) |
以5本不同的书籍举例, 表1是这5本书对应的欧氏距离初始矩阵.
| 表 1 欧式距离初始矩阵 |
(3) 凝聚式层次聚类
根据第(2)步得到的欧式距离矩阵, 选择距离最近的两个簇b1, b5. 合并b1, b5为簇{b1, b5},接着利用组平均准则, 选取其他簇与合并簇所有点之间距离的平均值作为下一步的邻近值, 更新欧式距离矩阵, 如表2所示.
| $\left\{\begin{array}{l} AVG.dis\tan ce(\{ b1,b5\} ,b2) = 3.525\\ AVG.dis\tan ce(\{ b1,b5\} ,b3) = 2.085\\ AVG.dis\tan ce(\{ b1,b5\} ,b4) = 3.46 \end{array}\right.$ |
| 表 2 迭代一次后的欧式距离矩阵 |
由表2合成新的合并簇{b2, b4},重复前面的步骤, 继续迭代更新矩阵.
| $\left\{\begin{array}{l} AVG.distance(\{ b2,b4\} ,b3) = 3.28\\ AVG.distance(\{ b1,b5\} ,\{ b2,b4\} ) = 3.4925 \end{array}\right.$ |
由表3合成新的合并簇{b1, b5, b3}, {b2, b4}, 最终聚类结果如图2所示, 可以直观地找到目标书籍的邻近集(和目标书籍在同一簇中的其他书籍), 根据邻近集书籍的评分预测目标书籍的可能获得的评分.
| 表 3 迭代两次后的欧式距离矩阵 |

|
图 2 书籍聚类结果树图示 |
评分预测:
| ${p_{ij}} = \overline {{p_j}} + \frac{{\displaystyle\sum\nolimits_{r \in S} {sim(j,r) \times \left( {{R_{i,r}} - \overline {{R_r}} } \right)} }}{{\displaystyle\sum\nolimits_{r \in S} {\left| {sim(j,r)} \right|} }}$ | (11) |
采用凝聚式层次聚类的基于项目的协同过滤算法流程图如图3所示.
3 实验结果与分析 3.1 实验数据集本文选用GroupLens提供的网络开源数据集MovieLens作为测试数据集[13], 整个数据集包括了六千多个电影观看者对3900多部电影的10万多条评价. 由三部分组成, 包括用户集, 电影集和用户-电影评分集.
3.2 实验评价标准本文采用Top-N推荐[14], 对推荐结果的质量用查准率Precision、查全率Recall来衡量, 计算方式如式(14)、(15).
| $Recall = \frac{{\displaystyle\sum\limits_{u \in U} {\left| {{R_{\left( u \right)}} \cap {T_{\left( u \right)}}} \right|} }}{{\displaystyle\sum\limits_{u \in U} {\left| {{T_{\left( u \right)}}} \right|} }}$ | (12) |
| $Precision = \frac{{\displaystyle\sum\limits_{u \in U} {\left| {{R_{\left( u \right)}} \cap {T_{\left( u \right)}}} \right|} }}{{\displaystyle\sum\limits_{u \in U} {\left| {{R_{\left( u \right)}}} \right|} }}$ | (13) |
其中,
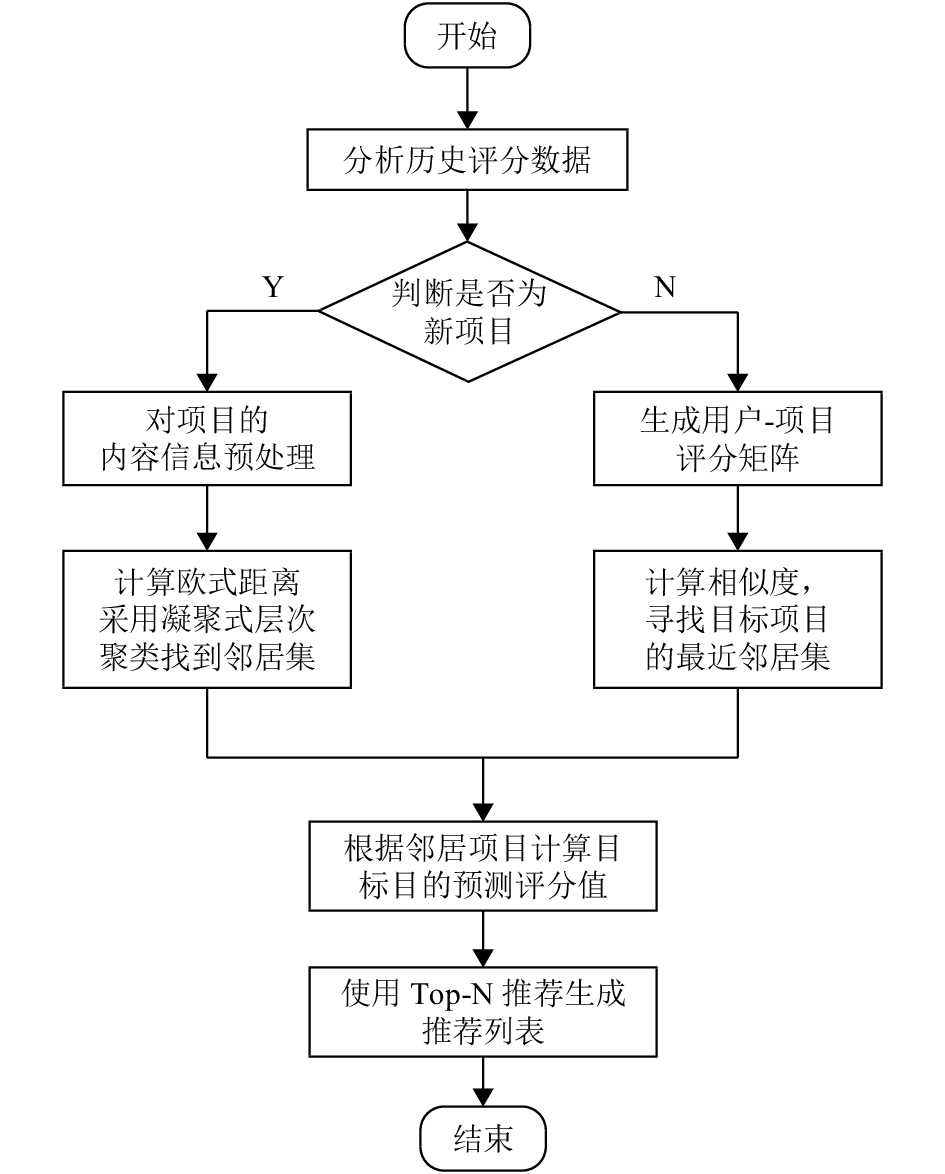
|
图 3 新项目冷启动算法 |
3.3 实验结果验证 3.3.1 新用户冷启动算法验证
本文实验以MovieLens数据集为例, 通过电影推荐验证新算法的性能. 将训练集和测试集的比例分为9:1, 新用户与老用户的比例设为3:7, 改变邻居数K值在5~40之间, 进行多组实验.
MovieLens的用户集中包含了性别、年龄、职业三项用户属性, 本文分析这三项特征信息, 计算出用户之间的特征差
| $attr(u,v) = \alpha \cdot sex + \beta \cdot age + \gamma \cdot occupation$ | (14) |
本文的α、β、γ皆取1/3, 满足式(6)的条件.
对User.data的预处理:
(1) 性别判定
MovieLens数据集中男性用户性别表示为M, 女性用户性别表示为F. 若两用户性别相同, sex取值为0, 若不同, sex取值为1.
(2) 年龄量化(表4)
| 表 4 MovieLens用户年龄的量化 |
(3) 职业量化(表5)
| 表 5 MovieLens用户职业的量化 |
由此, 式(14)中sex取值为0或1, age, occupation的取值为两用户特征值量化后差值的绝对值.
求得用户特征差值
传统协同过滤算法采用改进的余弦相似度User-IIF算法[15], 如式(17)所示, 降低了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响.
| ${w_{uv}} = \frac{{\displaystyle\sum\nolimits_{i \in {N_{(u)}} \cap {N_{(v)}}} {\frac{1}{{\log (1 + \left| {N(i)} \right|)}}} }}{{\sqrt {\left| {N(u)} \right|\left| {N(v)} \right|} }}$ | (15) |
求得相似度后, 计算预测评分, 为用户进行推荐. 进行多次实验, 求得多组评估指标, 并用Matlab进行仿真, 仿真结果如图4、图5所示.
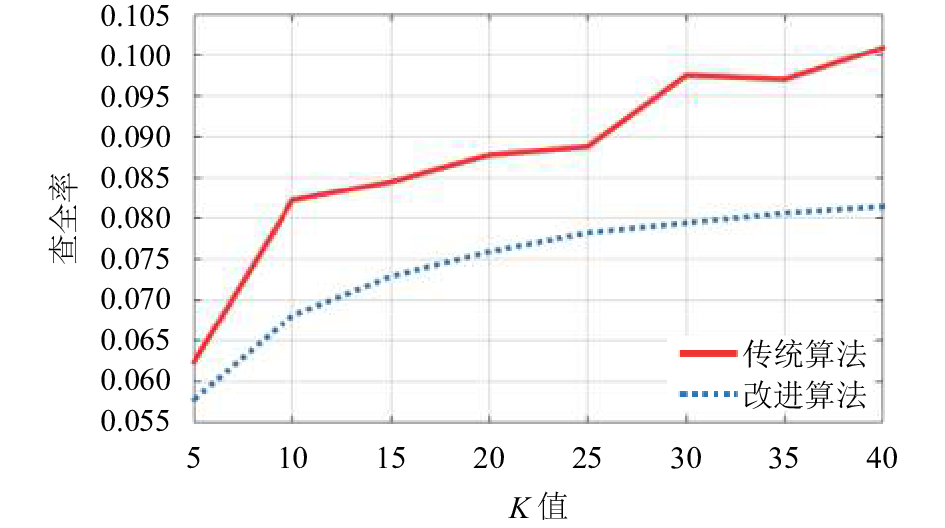
|
图 4 改进前后算法查全率随K值的变化 |
图4表示基于用户的协同过滤算法在新用户的情况下, 新算法与传统算法的查全率与邻居数的变化关系图. 由图可知, 随着邻居数K值增加, 系统的查全率呈上升趋势, 并且新算法的查全率高于传统算法, 说明新算法的检索结果更有效.

|
图 5 改进前后算法查准率随K值的变化 |
图5表示基于用户的协同过滤算法, 在新用户的情况下新算法与传统算法查准率与K值的关系. 可以看出, 新算法推荐结果的准确率高于传统算法. 改进后算法推荐精度更高, 有效地改善了系统新用户的冷启动问题.
结合图4、图5发现, 在改进后的User-based CF中, 当邻居数取35时算法查全率最大, 查准率也比较高, 算法推荐质量较好.
3.3.2 新项目冷启动算法验证本文提出的新项目的冷启动算法采用了凝聚式层次聚类的思想, 在MovieLens数据集上进行实验结果验证, 将训练集和测试集的比例分为9:1, 新项目和老项目的比例为3:7.
Step 1. 对movie.data的数据初始化处理.
(1) 年份(year)关键词: 直接表示为iy、jy.
(2) 派别(genres)关键词: 遍历电影所属的派别, 若两部电影有属于一个相同的派别, 则g值减1, 否则, g值保持不变(g初始值为3), 最后得到目标电影和其他电影派别上的距离g值.
Step 2. 欧式距离的计算.
在对电影的基本数据处理之后, 计算电影之间的欧几里德距离. 欧式距离计算如式(10).
Step 3. 层次聚类.
最后选取不同的邻居数K值在5~40之间, 进行多次实验比较加入新项目时, 改进前后基于项目的协同过滤算法在推荐精度上的变化, 如图6、图7所示.
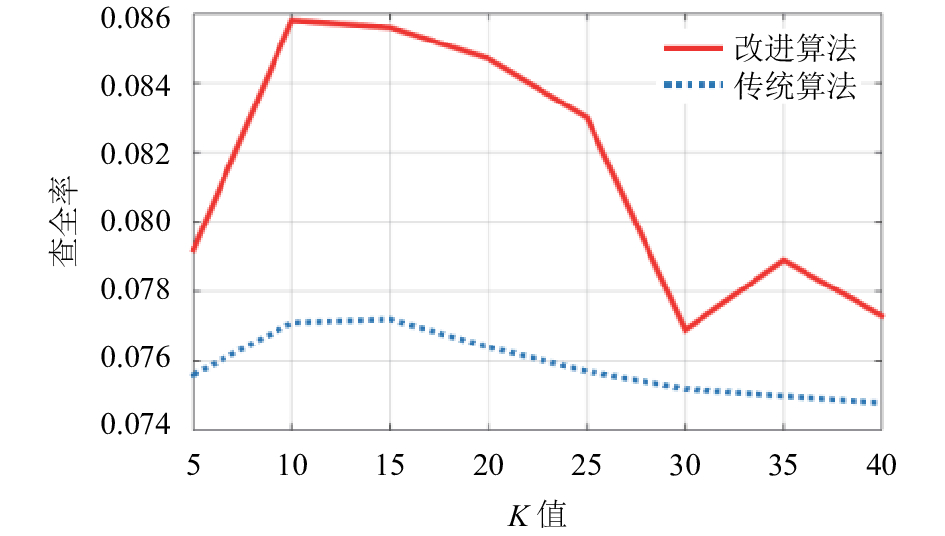
|
图 6 改进前后ItemCF算法查全率随K值的变化 |
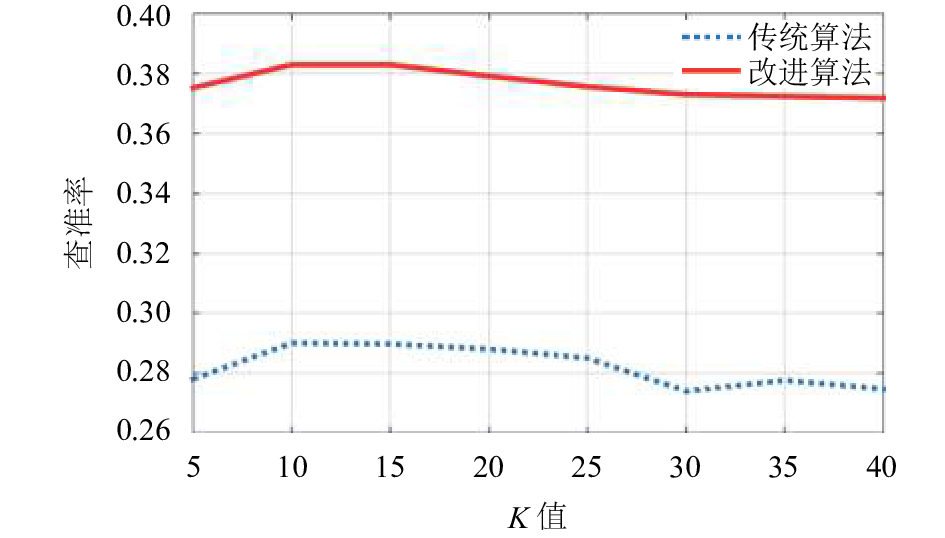
|
图 7 改进前后ItemCF算法查准率随K值的变化 |
传统方法采用的相似度计算公式如式(18), 减轻了热门物品和其他众多物品相似的可能性.
| ${w_{ij}} = \frac{{\left| {N(i) \cap N(j)} \right|}}{{\sqrt {\left| {N(i)} \right|\left| {N(j)} \right|} }}$ | (16) |
从图6可以看出, 采用了层次聚类的算法在查全率上优于传统算法, 在邻居数取10的时候, 查全率达到最大值, 在邻居数取25~35之间时, 查全率波动较大, 并且呈下降趋势. 整体上看, 改进后的层次聚类算法推荐结果中被检索到的更多, 查全率更高.
图7比较了采用凝聚式层次聚类的协同过滤和传统基于项目的协同过滤算法在查准率上的性能, 由图可见, 算法的查准率比较平稳, 在加入了新项目后, 改进后算法的查准率优于传统算法的值, 表现出更好的推荐精度.
结合图6、图7, 在改进后的Item-based CF中, 邻居数取10时, 算法的推荐性能较好.
4 结论本文首先介绍了协同过滤算法以及算法的冷启动问题, 重点对新用户和新项目的冷启动问题进行研究, 提出了融合用户信息模型的基于用户的协同过滤算法和采用层次聚类的基于项目的协同过滤算法. 具体研究工作如下:
(1) 针对新用户的冷启动, 算法提取了用户个人特征信息, 为用户信息建模, 调用Sigmoid函数求得基于用户特征模型的相似度.
(2) 对于新项目的冷启动, 算法提取项目的信息属性, 计算出欧式距离, 采用凝聚式层次聚类的方法, 找到目标项目的邻居项目, 计算预测评分, 完成推荐.
(3) 选用网络开源数据集MovieLens进行实验验证, 将新算法与传统算法多次实验对比. 结果表明, 在新用户和新项目的情况下, 新算法推荐结果的查全率、查准率都有所提升, 有效地缓解了传统协同过滤算法的冷启动问题, 改善了推荐质量.
| [1] |
Maes P. Agents that reduce work and information overload. Communications of the ACM, 1994, 37(7): 30-40. DOI:10.1145/176789.176792 |
| [2] |
Guo YY, Liu QC. E-commerce personalized recommendation system based on multi-agent. Proceedings of the 7th International Conference on Fuzzy Systems and Knowledge Discovery. Yantai, China. 2010. 1999–2003.
|
| [3] |
Bobadilla J, Ortega F, Hernando A. A collaborative filtering similarity measure based on singularities. Information Processing & Management, 2012, 48(2): 204-217. |
| [4] |
Hu R, Pu P. Enhancing collaborative filtering systems with personality information. Proceedings of the 5th ACM Conference on Recommender Systems. Chicago, IL, USA. 2011. 197–204.
|
| [5] |
Wang JW. A collaborative filtering systems based on personality information. Proceedings of 2015 International Industrial Informatics and Computer Engineering Conference. Xi’an, China. 2015.
|
| [6] |
Goldberg D, Nichols D, Oki BM, et al. Using collaborative filtering to weave an information tapestry. Communications of the ACM, 1992, 35(12): 61-70. DOI:10.1145/138859.138867 |
| [7] |
申辉繁. 协同过滤算法中冷启动问题的研究[硕士学位论文]. 重庆: 重庆大学, 2015.
|
| [8] |
马卓. 协同过滤推荐算法的研究与改进[硕士学位论文]. 秦皇岛: 燕山大学, 2015.
|
| [9] |
Xu JW, Yao Y, Tong HH, et al. RaPare: A generic strategy for cold-start rating prediction problem. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(6): 1296-1309. DOI:10.1109/TKDE.2016.2615039 |
| [10] |
Nguyen VD, Sriboonchitta S, Huynh VN. Using community preference for overcoming sparsity and cold-start problems in collaborative filtering system offering soft ratings. Electronic Commerce Research and Applications, 2017, 26: 101-108. DOI:10.1016/j.elerap.2017.10.002 |
| [11] |
Katarya R, Verma OP. Effective collaborative movie recommender system using asymmetric user similarity and matrix factorization. Proceedings of 2016 International Conference on Computing, Communication and Automation. Noida, India. 2016. 71–75.
|
| [12] |
乔雨, 李玲娟. 推荐系统冷启动问题解决策略研究. 计算机技术与发展, 2018, 28(2): 83-87. DOI:10.3969/j.issn.1673-629X.2018.02.019 |
| [13] |
http://www.grouplens.org/node/73.
|
| [14] |
程淑玉. 基于协同过滤算法的个性化推荐系统的研究[硕士学位论文]. 合肥: 合肥工业大学, 2010.
|
| [15] |
Breese JS, Heckerman D, Kadie C. Empirical analysis of predictive algorithms for collaborative filtering. Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence. Madison, WI, USA. 1998. 43–52.
|
 2019, Vol. 28
2019, Vol. 28


