近年来, 云计算技术发展迅速, 涌现出了一大批成熟的云计算服务平台. 基础设施即服务(IaaS)、平台即服务(PaaS)和软件即服务(SaaS)是云计算的三种主要的服务模式, 其中IaaS应用最广泛. IaaS采用虚拟化技术将物理服务器抽象成虚拟机, 并且通过互联网提供给云消费者使用, 云消费者采用按使用付费的方式租用虚拟机.

云提供商(Amazon EC2)向云消费者提供了两种计费策略, 按需实例和预留实例. 对于按需实例, 云消费者根据当前的工作负载动态获取, 按照实际使用情况付费. 对于预留实例, 云消费者需要预付部分费用, 并且在预留期间不管是否使用都需要付费. 通过权衡按需实例和预留实例的使用, 可以有效降低云消费者的资源使用成本. 因此, 云资源预留问题即为: 确定预留资源的数量, 以最小化云消费者的资源使用成本.

虚拟机整合问题旨在通过虚拟机的在线迁移, 在满足云消费者资源需求的前提下, 最小化所使用的物理服务器的数量, 以降低能耗, 实现绿色云计算. 师雪霖等人借鉴网络效用最大化模型, 提出了虚拟机放置的效用最大化模型, 并且将原始问题转化为拉格朗日对偶问题, 采用次梯度算法进行求解^[1]. 赵君等人同时考虑物理资源的浪费和网络总流量, 将虚拟机放置问题建模为多目标优化问题, 并且提出了一种基于多目标蚁群优化的虚拟机放置算法^[2]. Xiao等人提出了一种虚拟机放置的启发式算法, 引入了偏度的概念度量服务器中多种资源利用的不均衡性, 通过最小化偏度, 可以有效整合不同类型的工作负载, 提高服务器资源的整体利用率^[3]. Zhang等人考虑了服务器和负载的异构性, 提出了异构感知的云资源提供算法^[4].

本文从云消费者的角度研究云资源提供问题. Chaisiri等人考虑了需求和价格的不确定性, 将云资源提供问题建模为多阶段随机整数规划问题, 并且使用Benders分解算法进行求解^[5]. 冉泳屹等人使用大偏差理论在线估计过载概率, 根据过载概率动态调整按需实例的数量, 同时采用自回归模型确定预留实例的数量, 进一步降低云消费者的资源使用成本^[6]. 然而, 冉泳屹等人并没有给出云资源预留问题的数学描述, 并且在确定预留实例的数量时, 仅仅考虑了单一的实例类型. Hwang等人将云资源提供问题分成两个阶段, 在资源预留阶段, 通过一个启发式方法确定资源预留方案, 在按需分配阶段, 采用卡尔曼滤波器预测当前的资源需求^[7]. Hwang等人虽然给出了云资源预留问题的数学描述, 但是所提出的启发式算法仅仅考虑了一种虚拟机类型, 以确定最优的虚拟机预留数量的上界和下界. 在先前的研究中, 我们将云资源提供问题建模为两阶段的随机整数规划问题, 并转化为确定性的整数线性规划问题, 利用CPLEX软件进行求解, 但是其计算复杂度较高, 不适用于在线应用^[8].

本文从云消费者的角度研究云资源提供问题, 提出了一种采用随机规划模型的云资源分配算法. 首先, 同时考虑按需实例和预留实例, 采用两阶段随机整数规划对云资源提供问题进行建模. 然后, 采用抽样平均近似方法减少资源提供问题的场景数量, 降低计算复杂度, 并且提出了一种基于阶段分解的混合进化算法求解资源提供问题. 在仿真实验中, 基于真实的工作负载数据及Amazon EC2的定价模型评估所提出的云资源分配算法, 验证了所提出算法的有效性.

1 云资源提供问题 1.1 云计算环境

针对特定的服务, 云提供商提供了多种可供选择虚拟机类型, 令 $V = \{ {V_1}, {V_2}, \cdots, {V_N}\} $ 表示云提供商所提供的一组虚拟机类型, $N$ 为虚拟机类型的总数. 假设一个 ${V_i}$ 类型的虚拟机的资源配置为 ${R_i} = [{r_{i1}}, {r_{i2}}, \cdots, {r_{iM}}]$ , $M$ 为虚拟机所拥有的资源类型的总数. 令 ${C_i}$ 表示一个 ${V_i}$ 类型的虚拟机的服务容量, 定义为在给定的服务质量约束条件下, 一个 ${V_i}$ 类型的虚拟机所能支持的最大并发用户数或服务请求到达速率.

云提供商(Amazon EC2)提供了两种计费策略, 按需实例和预留实例. 对于按需实例, 云消费者根据当前的工作负载动态获取, 按照实际使用情况付费. 对于预留实例, 云消费者需要预付部分费用, 并且在预留期间不管是否使用都需要付费. 令按需实例的计费周期(短期规划周期)为 ${T_S}$ , 预留实例的计费周期(长期规划周期)为 ${T_L}$ , 令 $T = {T_L}/{T_S}$ . 假设一个 ${V_i}$ 类型的预留实例预付费用为 $P_i^R$ , 令 $p_i^R=P_i^R/T$ , 在预留期间每时间 ${T_S}$ 费用为 $p_i^r$ , 一个 ${V_i}$ 类型的按需实例每时间 ${T_S}$ 费用为 $p_i^o$ , 通常假设 $p_i^o > p_i^r + p_i^R$ .

1.2 基于随机规划的云资源提供问题

假设在第 $t(1 \leqslant t \leqslant T)$ 个短期规划周期, 云消费者的工作负载为 ${d_t}$ . 令 $R = \{ {n_1}, \cdots , {n_N}\} $ 表示长期规划周期的资源预留方案, 其中 ${n_i}$ 为 ${V_i}$ 类型的预留实例的数量, 预留的服务容量为 $r = \displaystyle \sum\nolimits_{i = 1}^N {{n_i}{C_i}} $ , 预留实例的使用成本为 $\displaystyle \sum\nolimits_{i = 1}^N {{n_i}P_i^R} +\displaystyle \sum\nolimits_{i = 1}^N {{n_i}p_i^rT} $ . 在短期规划周期, 若预留的服务容量能够满足工作负载需求, 则不需要动态分配按需实例, 否则, 需要动态分配按需实例, 按需实例的使用成本为

$ \left\{\begin{gathered} Q(\{ {n_i}\} , {d_t}) = \mathop {\min }\limits_{{x_i}} \sum\nolimits_{i = 1}^N {{x_i}p_i^o} \\ {\rm{ s.t.}}\sum\nolimits_{i = 1}^N {{x_i}{C_i}} \geqslant {d_t} - \sum\nolimits_{i = 1}^N {{n_i}{C_i}} \\ {x_i} \in {N_0} \\ \end{gathered} \right.$

(1)

其中, ${x_i}$ 表示 ${V_i}$ 类型的按需实例的数量. 问题(1)是短期规划周期的按需资源分配问题, 即给定资源预留方案和当前的工作负载, 动态分配按需实例, 在满足工作负载需求的条件下, 最小化按需实例的使用成本.

云资源提供问题可以描述为

$\left\{\begin{aligned} &\mathop {\min }\limits_{{n_i}} \sum\nolimits_{i = 1}^N {{n_i}P_i^R} + \sum\nolimits_{i = 1}^N {{n_i}p_i^rT} + \sum\nolimits_{t = 1}^T {Q(\{ {n_i}\} , {d_t})} \\ &{\rm{ s.t.}}\;\;{n_i} \in {N_0} \end{aligned} \right.$

(2)

其中目标函数为长期规划周期中预留实例和按需实例总的使用成本. 问题(2)依赖于长期规划周期的工作负载情况, 使用云消费者的工作负载历史数据, 可以对工作负载的概率分布 ${p_D}({D_k})$ 进行估计, 其中 ${D_k}, k = 1, 2, \cdots ,$ $ K, ({D_1} < {D_2} < \cdots < {D_K})$ 为工作负载所有可能的取值. 因此, 问题(2)可以转化为

$\left\{\begin{aligned} &\mathop {\min }\limits_{{n_i}} \sum\nolimits_{i = 1}^N {{n_i}p_i^R} + \sum\nolimits_{i = 1}^N {{n_i}p_i^r} + \sum\nolimits_{k = 1}^K {{p_D}({D_k})Q(\{ {n_i}\} , {D_k})} \\ &{\rm{ s.t.}}\;\;{n_i} \in {N_0} \\ \end{aligned}\right. $

(3)

其中目标函数为每个短期规划周期中预留实例和按需实例的平均使用成本. 问题(3)是一个两阶段的随机整数规划问题. 在资源预留阶段, 需要根据长期规划周期的工作负载情况, 确定预留实例的类型和数量, 在按需分配阶段, 需要根据当前的工作负载, 确定动态分配的按需实例的类型和数量.

问题(3)可以转化为一个确定性的整数线性规划问题,

$\left\{\begin{aligned} & \mathop {\min }\limits_{{n_i}} \sum\nolimits_{i = 1}^N {{n_i}p_i^R} + \sum\nolimits_{i = 1}^N {{n_i}p_i^r} + \sum\nolimits_{k = 1}^K {[p({D_k})\sum\nolimits_{i = 1}^N {{x_{ki}}p_i^o} ]} \\ & {\rm{s.t.}}\;\;\sum\nolimits_{i = 1}^N {{n_i}{C_i}} + \sum\nolimits_{i = 1}^N {{x_{ki}}{C_i}} \geqslant {D_k},\; {n_i} \in {N_0}, {x_{ki}} \in {N_0} \end{aligned}\right. $

(4)

问题(4)被称为问题(3)的确定性等价问题, 可以通过CPLEX软件进行求解.

2 云资源分配算法 2.1 抽样平均近似问题

当工作负载D取值(随机规划问题的场景)的数量很大, 甚至可能是一个连续的随机变量时, 问题(3)中的随机规划问题将不易求解. 为了求解这个复杂的问题, 可以使用抽样平均近似方法. 抽样平均近似方法对场景进行抽样, 减少场景数量, 降低求解复杂度. 常用的抽样方法包括蒙特卡罗方法、拟蒙特卡罗方法和均匀离散化方法等. 因为工作负载D是一个一维的随机变量, 所以这里使用均匀离散化方法^[9].

在均匀离散化方法中, 将整个概率区间 $[0, 1]$ 均匀离散化, 生成N_S个等间隔的离散概率点p_j=(2j–1)/(2N_S),j=1, …, N_S, 对于每一个 ${p_j}$ , 找到最小的 ${k_j}(1 \leqslant {k_j} \leqslant K)$ , 使得 $\displaystyle \sum\nolimits_{k = 1}^{{k_j}} {{p_D}({D_k})} \geqslant {p_j}$ , 则 ${D_{{k_j}}}$ 为工作负载D的第 $j$ 个抽样. 由D的 ${N_S}$ 个抽样, 问题(3)可以近似表示为

$\left\{\begin{aligned} &\mathop {\min }\limits_{{n_i}} \sum\nolimits_{i = 1}^N {{n_i}p_i^R} + \sum\nolimits_{i = 1}^N {{n_i}p_i^r} + \frac{1}{{{N_S}}}\sum\nolimits_{j = 1}^{{N_S}} {Q(\{ {n_i}\} , {D_{{k_j}}})} \\ &{\rm{ s.t.}}\;\;{n_i} \in {N_0} \end{aligned} \right.$

(5)

上述问题被称为问题(3)的抽样平均近似问题, 该问题仍然是一个两阶段的随机整数规划问题, 可以转化为一个确定性的整数线性规划进行求解, 并且样本容量 ${N_S}$ 越大, 抽样平均近似问题的近似精度越高.

2.2 混合进化算法

虽然抽样平均近似方法可以减少场景数量, 有效降低求解复杂度, 但是问题(5)转化为确定性等价的整数规划问题之后, 规模仍然很大, 不采用分解算法很难求解. 本文提出了一种基于阶段分解的混合进化算法, 使用进化算法对第一阶段决策变量进行搜索, 对于第二阶段子问题使用整数规划进行求解. 因此, 问题(5)可以分解为:

主问题:

$\left\{\begin{aligned} & \mathop {\min }\limits_{{n_i}} \sum\nolimits_{i = 1}^N {{n_i}p_i^R} + \sum\nolimits_{i = 1}^N {{n_i}p_i^r} + \frac{1}{{{N_S}}}\sum\nolimits_{j = 1}^{{N_S}} {Q(\{ {n_i}\} , {D_{{k_j}}})} \\ &{\rm{ s.t.}}\;\;{n_i} \in {N_0} \\ \end{aligned}\right. $

(6)

子问题:

$\left\{\begin{aligned} & Q(\{ {n_i}\} , {D_{{k_j}}}) = \mathop {\min }\limits_{{x_i}} \sum\nolimits_{i = 1}^N {{x_i}p_i^o} \\ &{\rm{ s.t.}}\sum\nolimits_{i = 1}^N {{x_i}{C_i}} \geqslant {D_{{k_j}}} - \sum\nolimits_{i = 1}^N {{n_i}{C_i}}, {x_i} \in {N_0} \\ \end{aligned} \right.$

(7)

在主问题中需要确定预留实例的类型和数量, 在子问题中需要确定按需实例的类型和数量, 子问题的决策依赖于主问题的决策, 并且对于主问题中给定的虚拟机预留配置, 子问题是 ${N_S}$ 个小规模的整数线性规划问题. 对于第一阶段主问题, 使用进化算法进行求解, 对于第二阶段子问题, 使用标准的整数线性规划求解方法进行求解.

接下来重点研究基于遗传算法的主问题求解方法. 遗传算法的关键是编码方案、适应度函数及遗传算子的设计^[10].

(1) 染色体编码

在进行遗传操作之前, 首先需要对优化问题的可行解进行编码. 常用的编码方法有二进制编码、格雷码编码和实数编码等, 其中二进制编码存在汉明悬崖问题, 格雷码编码在进行交叉操作时会产生更高阶的非线性. 为了克服这些问题, 这里采用实数编码方案. 对于问题(6)的一个可行解 $({n_1}, {n_2}, \cdots, {n_N})$ , ${n_i} \in {N_0}$ 且 $0 \leqslant {n_i} \leqslant n_i^{\max }$ , 其中 $n_i^{\max } = \left\lceil {{D_{\max }}/{C_i}} \right\rceil $ , ${D_{\max }}$ 为工作负载需求的最大值, ${n_i}$ 可以用一个实数变量 ${x_i}$ 表示 $0 \leqslant {x_i} $ . 因此, 可行解 $< n_i^{\max } + 1({n_1}, {n_2}, \cdots, {n_N})$ 可以编码为 $({x_1}, {x_2}, \cdots, {x_N})$ .

(2) 适应度函数

适应度函数用于评价种群中个体对环境的适应程度, 也就是可行解的优劣, 可行解越好, 适应度函数值越大. 问题(6)是一个最小化问题, 以总的资源提供成本最小化为优化目标. 对于可行解 $({n_1}, {n_2}, \cdots, {n_N})$ , 适应度函数 $f({n_1}, \cdots, {n_N})$ 定义为

$f({n_1}, \cdots, {n_N}) = \frac{1}{{1 + T({n_1}, \cdots, {n_N}) - {T_{\min }}}}$

(8)

其中, $T({n_1}, \cdots, {n_N})$ 是虚拟机预留配置为 $({n_1}, \cdots, {n_N})$ 时总的资源提供成本, ${T_{\min }}$ 是到目前为止所获得的目标函数的最小值. 为了确定 $T({n_1}, \cdots, {n_N})$ , 需要求解 ${N_S}$ 个子问题(7).

(3) 选择

选择算子实现种群的优胜劣汰, 既要保证一定的选择强度, 使得种群向着最优解进化, 又要保持种群的多样性, 防止未成熟收敛. 常用的选择算子有适应度比例选择、锦标赛选择和排序选择等. 根据Blickle等人^[11]的研究, 指数排序选择算子能够在相同的选择强度条件下, 保证较好的种群多样性, 避免算法陷入局部最优解, 因此本文采用指数排序选择算子. 在指数排序选择操作中, 首先对种群中所有个体按照适应度值升序排列, 然后按照个体的顺序为其分配相应的选择概率

${p_i} = \frac{{c - 1}}{{{c^N} - 1}}{c^{N - i}}$

(9)

其中, $c = {p_i}/{p_{i + 1}}(0 < c < 1)$ 是相邻两个个体选择概率的比值, $c$ 值越小, 选择算子的选择强度越大. 在确定了每个个体的选择概率之后, 使用轮盘赌采样法选择个体.

(4) 交叉

交叉操作是遗传算法的关键步骤, 决定了遗传算法的全局搜索能力. 本文采用模拟二进制交叉算子(SBX)^[12], 对于大多数优化问题具有良好的全局搜索能力. 在SBX操作中, 对于两个父个体 ${\beta _i} = ({\beta _{i1}}, {\beta _{i2}}, \cdots, {\beta _{iN}})$ 和 ${\beta _j} = ({\beta _{j1}}, {\beta _{j2}}, \cdots, {\beta _{jN}})$ , 两个子个体 ${\beta '_i}$ 和 ${\beta '_j}$ 定义为

$\left\{\begin{gathered} {{\beta '}_{ik}} = \frac{1}{2}[(1 + {B_k}){\beta _{ik}} + (1 - {B_k}){\beta _{jk}}] \\ {{\beta '}_{jk}} = \frac{1}{2}[(1 - {B_k}){\beta _{ik}} + (1 + {B_k}){\beta _{jk}}] \\ \end{gathered} \right.$

(10)

其中, ${B_k}$ 定义为

${B_k} = \left\{ {\begin{array}{*{20}{l}} {{{(2 \cdot u)}^{\frac{1}{{\eta +1}}}},\;\;u \leqslant \frac{1}{2}} \\ {{{\left( {\frac{1}{{2 \cdot (1 - u)}}} \right)}^{\frac{1}{{\eta + 1}}}},\;\;u > \frac{1}{2}} \end{array}} \right.$

其中, $u$ 是 $[0, 1]$ 上均匀分布的随机数, $\eta $ 取值为2.

(5) 变异

变异算子决定了遗传算法的局部搜索能力, 同时也维持了种群的多样性. 常用的变异算子有均匀变异、高斯变异和Breeder变异等. 均匀变异和高斯变异的性能依赖于参数的自适应调整, Breeder变异的性能稍差, 但是更容易实施. 在Breeder变异操作中,

${n'_i} = {n_i} \pm (0.5 \cdot rang{e_i} \cdot \theta )$

(11)

其中, 正负号以相等的概率随机选择, $rang{e_i}$ 是 ${n_i}$ 的取值范围, $\theta $ 定义为

$\theta = \sum\limits_{m = 1}^M {a(m) \cdot {2^{ - (m-1)}}} $

其中, $a(m)$ 以概率 $1/M$ 取值为1, 以概率 $1 - 1/M$ 取值为0.

遗传算法的流程为:

参数设置: 在遗传算法中, 种群规模 $N$ 、交叉概率 ${p_c}$ 和变异概率 ${p_m}$ 与算法的性能密切相关. 通常: 种群规模设置为大于变量数的10倍, 交叉概率设置为0.7–0.8之间, 变异概率设置为变量数的倒数^[10].

步骤1. 随机生成问题(6)的 $N$ 个可行解作为初始种群;

步骤2. 使用指数排序选择法选择当前种群中的个体进行复制, 执行 $N$ 次, 生成 $N$ 个个体;

步骤3. 将选择-复制操作生成的 $N$ 个个体进行随机配对, 对每一对个体, 以交叉概率 ${p_c}$ 执行SBX操作;

步骤4. 对交叉操作生成的每一个个体, 以变异概率 ${p_m}$ 执行Breeder变异操作;

步骤5. 判断是否满足终止条件, 若满足则终止遗传算法, 否则返回步骤2继续执行遗传算法.

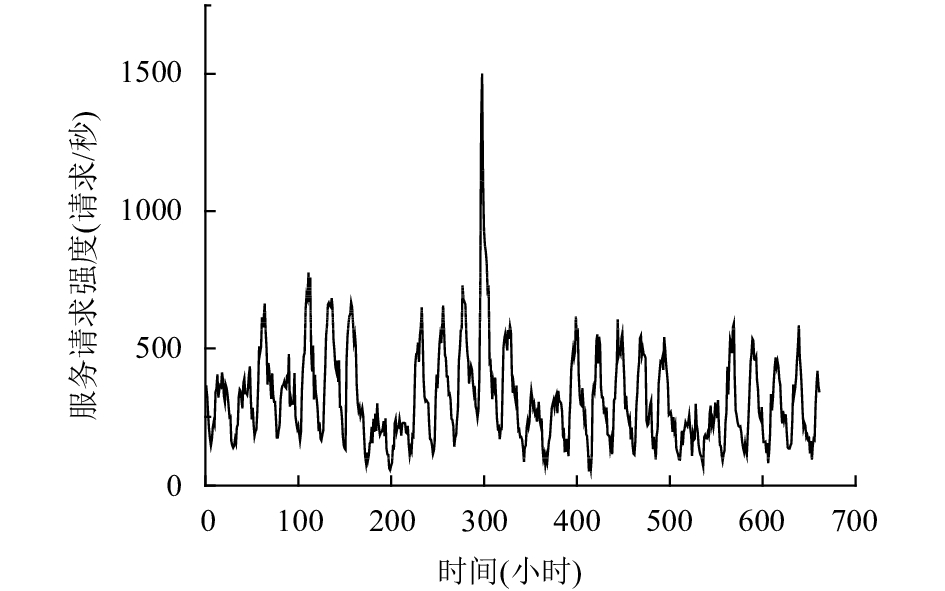
3 仿真实验

使用某网站一个月的工作负载历史数据作为实验数据, 如图1所示. 根据工作负载历史数据, 可以对工作负载的概率分布进行估计, 结果如图2所示. 针对Web服务, 云提供商(Amazon EC2)提供了4种类型的虚拟机: Small(m1.small), Medium(m1.medium), Large(m1.large), Extra Large(m1.xlarge), 它们的计费策略和服务能力^[7]如表1所示.

3.1 资源预留方案对运营成本的影响

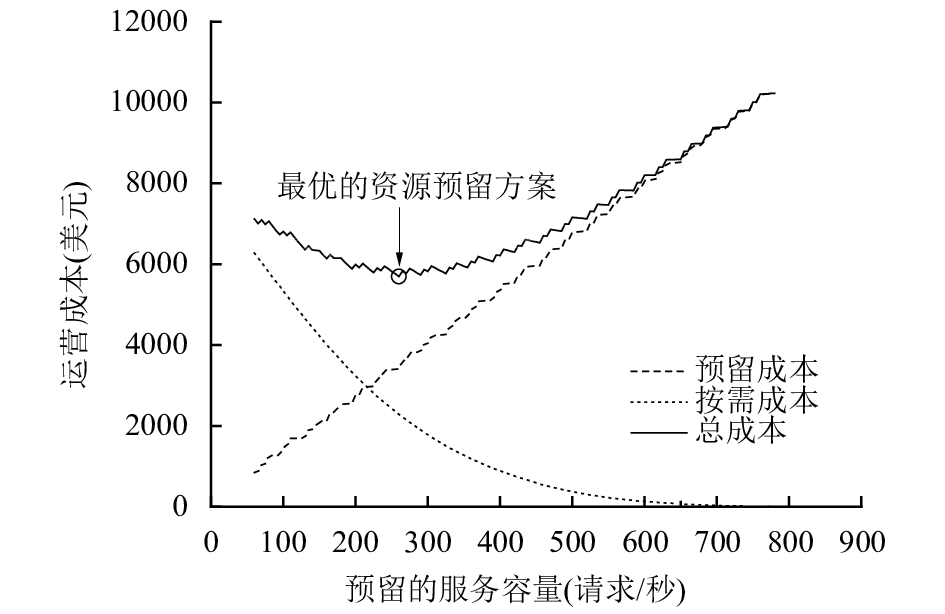
首先分析资源预留对云消费者的资源使用成本的影响. 研究不同的资源预留方案下云消费者的资源使用成本, 结果如图3所示. 从图中可以看出, 最优的资源预留方案为 $\{ {n_1} = 0, {n_2} = 0, {n_3} = 4, {n_4} = 0\} $ , 预留的服务容量为260请求/秒, 资源使用成本为5694美元. 随着预留资源的增加, 预留实例的使用成本逐渐增大, 按需实例的使用成本逐渐减小, 在预留资源太多或者太少时资源使用成本均比较高, 这是因为在预留资源太多时, 预留实例得不到充分使用, 造成资源浪费, 在预留资源太少时, 需要使用更多的按需实例.

3.2 抽样平均近似方法

接下来分析抽样平均近似方法的性能, 比较均匀离散化方法与蒙特卡罗方法及拟蒙特卡罗方法的近似精度, 并讨论抽样点数对近似精度的影响, 结果如图4所示. 从图中可以看出, 抽样点数越大, 抽样平均近似方法的近似精度越高, 在相同的抽样点数下, 均匀离散化方法比蒙特卡罗方法及拟蒙特卡罗方法的近似精度更高, 当抽样点数 ${N_S} = 10$ 时, 均匀离散化方法的近似精度达到99%. 因此, 选择均匀离散化方法, 并且选取抽样点数 ${N_S} = 10$ .

3.3 混合进化算法

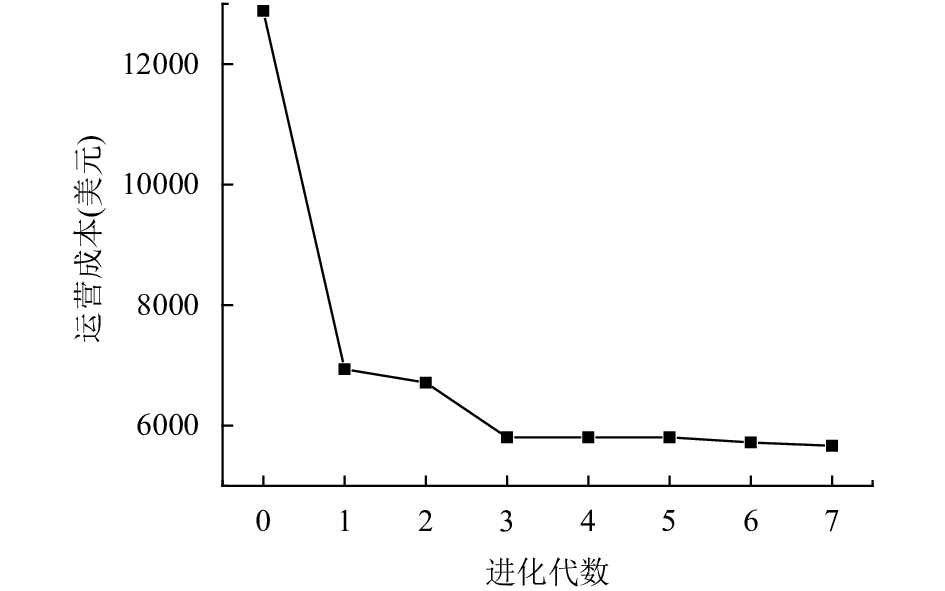
最后分析混合进化算法的性能. 从图5可以看出, 随着进化代数的增加, 所获得的资源预留方案逐渐趋向于最优的资源预留方案, 当进化代数 $G \geqslant 7$ 时, 所获得的资源预留方案即为最优的资源预留方案. 因此, 混合进化算法的终止条件选为 $G = 20$ . 比较本文所提出的混合进化算法和Hwang等人所提出的启发式算法的性能, 二者均可获得最优的资源预留方案, 节省了超过25%的运营成本, 但是Hwang等人的方法需要针对搜索范围内的每个资源预留方案, 确定总的运营成本, 所以求解过程所消耗的时间更长, 并且当最优解不在搜索范围内时不能获得最优的资源预留方案.

4 总结

本文针对云资源提供问题, 提出了一种采用随机规划模型的云资源分配算法, 在满足云消费者资源需求的条件下, 最小化其资源使用成本. 首先, 同时考虑按需实例和预留实例, 采用两阶段随机整数规划对云资源提供问题进行建模. 然后, 采用抽样平均近似方法和基于阶段分解的混合进化算法求解云资源提供问题. 基于真实的工作负载数据及Amazon EC2的定价模型验证所提出的云资源分配算法. 仿真实验结果表明, 所提出的云资源分配算法能够在较短时间内获得近似最优的云资源预留方案, 有效降低了云消费者的资源使用成本.