2. 江苏南水科技有限公司, 南京 210012;
3. 云南省水文水资源局西双版纳分局, 西双版纳 666100
2. Jiangsu Nanshui Technology Co. Ltd., Nanjing 210012, China;
3. Xishuangbanna Branch, Yunnan Provincial Hydrographic and Water Resources Bureau, Xishuangbanna 666100, China
随着数字技术、通信技术的不断发展, 数字图像、视频等多媒体交流形式在人们日常生活中扮着相当重要的角色[1]. 然而在通信传输过程中, 这些信息的安全性面临到巨大的威胁. 相比现代数字图像具有海量数据、高度相关性的特点, 一些传统的加密算法已不适用于图像加密[2,3]. 由于混沌系统是非线性的动力系统, 具有初值敏感性、遍历性、随机性等特点, 与图像加密非常契合, 被广泛应用于图像加密领域[4–9].
文献[10]提出了一种多混沌映射的快速图像加密算法, 该算法加密效率较高. 文献[11]提出了一种利用复合混沌系统的加密算法, 由于低维混沌系统控制参数和初始值个数少, 安全性很低. 文献[12]采用超混沌系统进行图像加密, 密钥空间大, 安全性较高, 但是单一的混沌系统, 算法复杂度低, 不能满足现代图像加密的要求. 文献[13]采用模拟DNA生物操作的方式, 通过伪DNA计算来实现信息加密, 成为信息加密算法的新热点. 文献[14]提出了结合混沌系统和DNA动态编码的图像加密算法, 然而由于DNA运算规则单一, 导致加密算法复杂度不够.
结合上述, 针对低维混沌系统和单一的DNA加密方案的空间小、复杂度低等问题, 本文提出一种结合多混沌与DNA的彩色图像加密算法, 采用超混沌系统实现了多种DNA编码方式加密. 通过仿真实验测试, 本文提出的图像加密算法具备足够大的密钥空间, 大大地增强了复杂度, 足以抵御各种攻击, 安全性更高.
1 混沌系统 1.1 Logistic映射Logistic映射是一个经典的非线性迭代方程, 其数学表达式如式(1)所示:
| ${x_{k + 1}} = \mu {x_k}(1 - {x_k})$ | (1) |
其中, 当3.5699<

|
图 1 系统状态随参数
|
1.2 Arnold映射
Arnold映射是一种非线性二维映射方程[9], 其公式定义如下:
| $\left[ {\begin{array}{*{20}{c}} {x'} \\ {y'} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&a \\ b&{ab + 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right]od N$ | (2) |
其中, (x, y)为明文图像的像素点,
Chen超混沌系统方程如下:
| $\left\{ {\begin{array}{*{20}{l}} {x = a(y - x) + w} \\ {y = dx - xz + cy} \\ {z = xy - bz} \\ {w = yz + ew} \end{array}} \right.$ | (3) |
式中, x, y, z, w是系统的状态变量; a, b, c, d, e是系统的控制参数. 当a=35, b=3, c=12, d=7, e处于[0.085, 0.798]区间内, Chen系统处于超混沌状态. 其混沌吸引子图如图2所示.
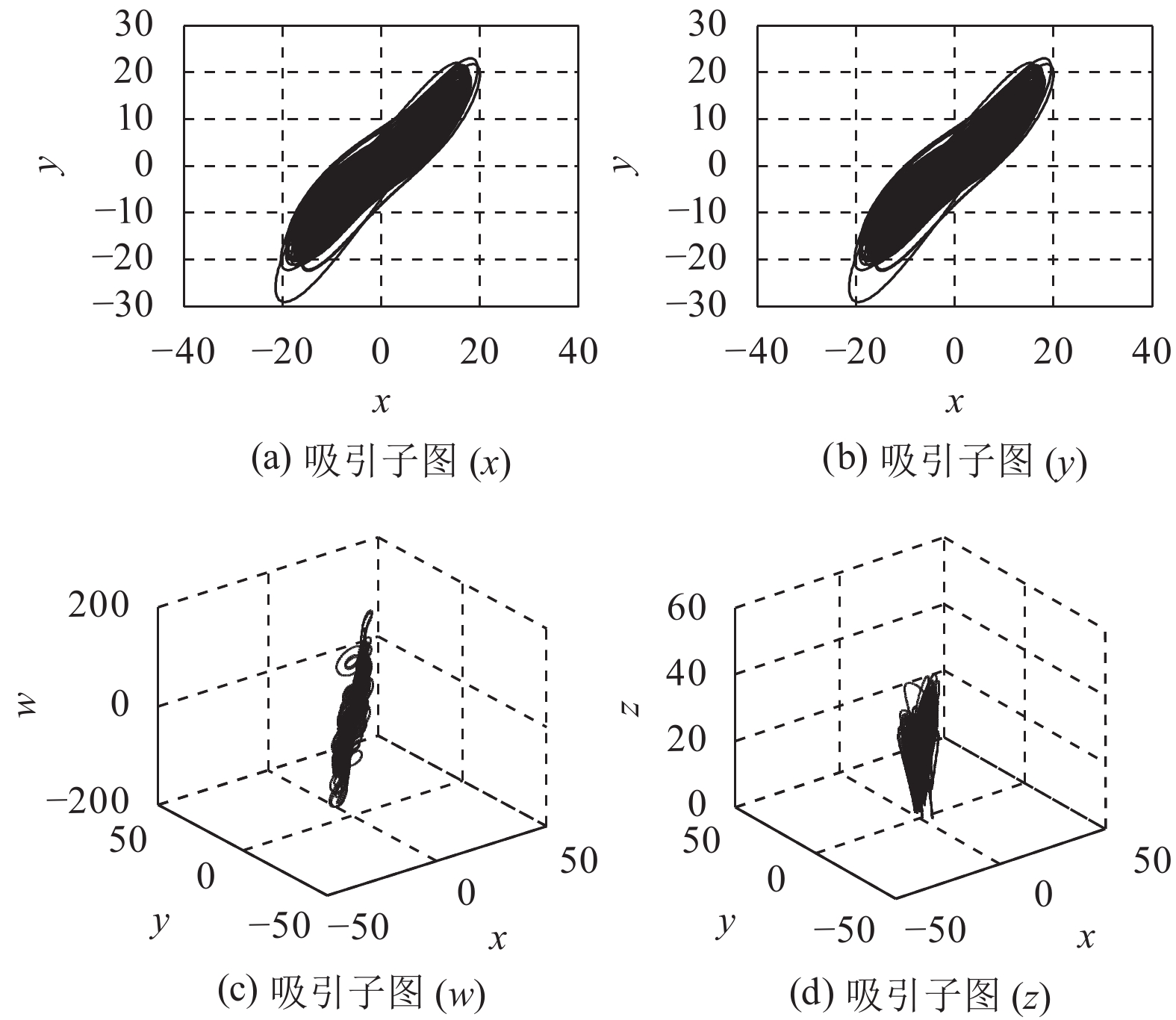
|
图 2 吸引子图 |
2 DNA编码技术
DNA中含4种不同的氮碱基分别是腺嘌呤A、胸腺嘧啶T、胞嘧啶C和鸟嘌呤G. 根据碱基互补配对原, 中A和T互补配对, C和G互补配对, 而数字图像中像素点的值可以用二进制表示, 在二进制中0和1是互补的, 因此00和11是互补的, 01和10是互补的. 基于这种思想, 结合二进制和DNA编码共有8种符合碱基编码规则, 如表1所示. 按照表1的方式, A用00表示, T用11表示, C用01来表示, G用10来表示. DNA的运算规则如表2~表4所示.
3 算法原理本文算法分成2个部分: Arnold置乱部分和DNA加密部分. 假设明文图像的大小为M×N, 具体步骤如下:
| 表 1 编码规则方式 |
| 表 2 DNA加法运算 |
| 表 3 DNA减法运算 |
| 表 4 DNA异或运算 |
第1步: 输入原始图像, 并进行R、G、B分层.
第2步: 对原始明文图像的R、G、B分量分别进行Arnold变换置乱, 得到R、G、B共3个分量的Arnold置乱图.
第3步: 将Logistic混沌系统方程迭代300次, 以减少暂态效应带来的不良影响, 设定初值和参数, 连续迭代式(1)方程得到长度为M×N的序列
第4步: 通过式(4)让序列
| ${{g(k)}} = {{floor}}({{g(k)}} \times {10^3})\;{\rm{mod }}\;256$ | (4) |
第5步: 对3个分量的Arnold置乱图和随机矩阵R均匀分成4×4的小块.
第6步: 设定好Chen系统的4个初值x(0)、y(0)、z(0) 和w(0), 利用四阶龙格-库塔算法对Chen系统方程求解可得到3个混沌序列
第7步: 将置乱图像矩阵各分块内所有像的灰度值转化为二进制数; 利用序列x(k)变换后的值, 按表1的第x(k)的DNA编码规则进行DNA编码, x(k)按照式(5)进行变换.
| ${{x(k)}} = ({{floor}}(x(k) \times {10^4})od 8) + 1$ | (5) |
| ${{y(k)}} = ({{floor}}({{y}}(k) \times {10^4})od 8) + 1$ | (6) |
同理, 将随机矩阵各分块内所有像素的灰度值转化为二进制数; 利用序列y(k)变换后的值, 按表1的第y(k)的DNA编码规则进行DNA编码, y(k)按照式(6)进行变换.
第8步: 图像矩阵与随机矩阵之间的DNA运算方式由序列
| ${{z(k)}} = {{floor}}({{z}}(k) \times {10^4})od 3$ | (7) |
当z(k)=0时, 则图像矩阵与随机矩阵分块内所有像素一一对应进行DNA加法运算.
当z(k)=1, 则图像矩阵与随机矩阵分块内所有像素一一对应进行减法运算.
当z(k)=2为则图像矩阵与随机矩阵分块内所有像素一一对应进行异或运算.
第9步: 将3个密文R、G、B分量合成, 得到最终密文图像.
解密算法是加密算法的反向过程, 只要在获取正确密钥条件下就能恢复出原始明文图像.
4 仿真实验本文算法采用大小为256×256×3的Lena彩色图像作为样本原始图像, 测试坏境为Windows10 64位系统坏境, 在Matlab 2016a软件平台下进行仿真实验, 运行得到的加密图像, 如图3所示.
5 算法分析 5.1 直方图分析图4分别为Lena图像R、G、B信道的明文和密文灰度直方图. 从图4可知, 加密前后图像直方图变化很大, 明文图像的直方图分布不均, 密文图像的直方图分布平均, 有效地隐藏了原始图像的灰度信息, 从密文的直方图上无法得到原始图像的统计特性.
5.2 密钥空间分析一个良好的加密算法, 须具有尽可能大的密钥空间[15]. 本文加密算法采用Logistic映射的有1个控制参数和1个初始值, 采用Chen系统有4个控制参数和4个初始值. 假如仿真实验计算机的每个参数精度都可达

|
图 3 图像加密结果 |
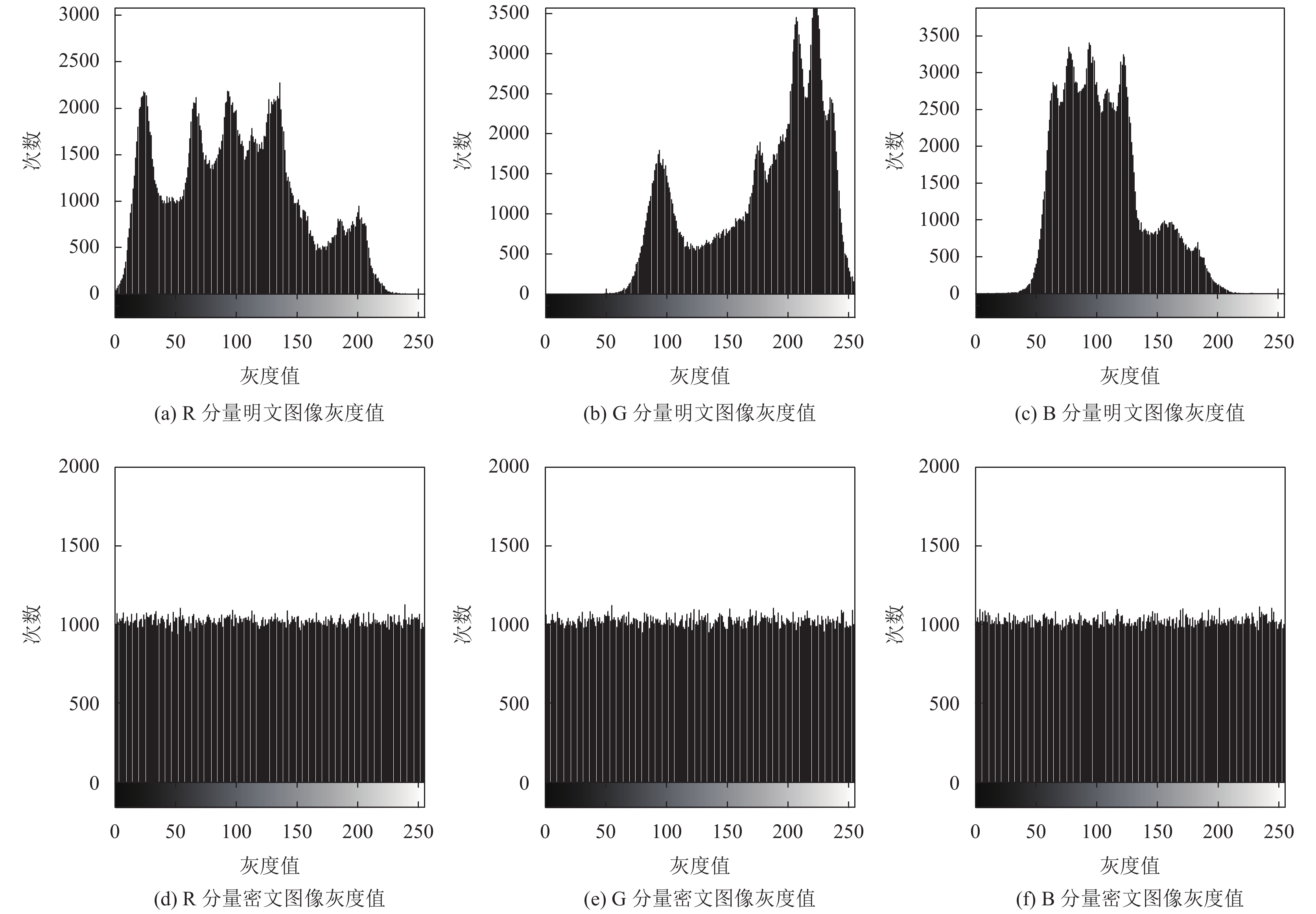
|
图 4 图像加密前后的灰度值 |
5.3 信息熵
信息熵是衡量信源随机性的重要参数, 图像混乱越厉害, 信息熵越接近理想值[16], 其计算公式为:
| $H(m) = \sum\limits_{i = 1}^{2N - 1} {P({m_i})} {\log _2}\frac{1}{{P({m_i})}}$ | (8) |
其中,
为了分析加密前后图像相邻像素之间的相关性, 分别从加密前后图像随机水平, 垂直, 对角3个方向上选取2000对相邻的像素, 使用式(9)计算像素相关性:
| $\left\{ {\begin{aligned} & {D(x) = 1/n\sum\limits_{i = 1}^n {[{x_i} - E(x)]} } \\ & {\operatorname{cov} (x,y) = 1/n\sum\limits_{i = 1}^n {[{x_i} - E(x)][{y_i} - E(y)]} } \\ & {r = \operatorname{cov} (x,y)/(\sqrt {D(x)} \sqrt {D(y)} )} \end{aligned}} \right.$ | (9) |
式中, n是像素点的个数; E(x), E(y)分别是x, y的期望, cov(x, y)是x, y的协方差, r是相关系数. 从表5可知, 原始明文图像的相邻像素高度相关, 其3个相关系数接近1, 而密文图像的3个相关系数趋近于0, 说明密文图像的相邻像素点基本不相关了. 与此同时比较其他算法[7,9], 得到本文加密算法的相关系数r更小.
| 表 5 像素相关系数 |
5.5 抗噪声分析
密文图像在传输过程中经常受到噪声, 造成图像失真. 为了检测算法抗噪声性能, 在密文图像上加了分差不同的高斯噪声. 从图5可以看出, 随着高斯噪声分差增加, 解密图像局部越来越模糊, 但是依然可以看清楚图像的轮廓信息, 可见本文算法具有较好的抗噪声性.

|
图 5 加入噪声后解密图像 |
6 结束语
本文提出一种结合多混沌与DNA的彩色图像加密算法, 采用超混沌系统实现了多种DNA编码方式加密. 通过仿真实验测试, 本文加密算法密钥空间较大, 大大地增强了复杂度, 足以抵御各种攻击, 安全性更高, 抗噪声性较好, 适合用于图像的加密传输, 具有良好的实用价值和应用前景.
| [1] |
张晓强, 王蒙蒙, 朱贵良. 图像加密算法研究新进展. 计算机工程与科学, 2012, 34(5): 1-6. DOI:10.3969/j.issn.1007-130X.2012.05.001 |
| [2] |
Parah SA, Ahad F, Sheikh JA, et al. Hiding clinical information in medical images: a new high capacity and reversible data hiding technique. Journal of Biomedical Informatics, 2017, 66: 214-230. DOI:10.1016/j.jbi.2017.01.006 |
| [3] |
田玉萍. 混沌神经元耦合置乱神经元的图像加密算法研究. 包装工程, 2014, 35(15): 105-112. |
| [4] |
朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法. 电子与信息学报, 2012, 34(7): 1735-1743. |
| [5] |
张健, 房东鑫. 应用混沌映射索引和DNA编码的图像加密技术. 计算机工程与设计, 2015, 36(3): 613-618. |
| [6] |
王倩. 基于位分解和超混沌映射的医学图像加密研究. 计算机仿真, 2019, 36(1): 209-212, 353. DOI:10.3969/j.issn.1006-9348.2019.01.043 |
| [7] |
Kanso A, Ghebleh M. An efficient and robust image encryption scheme for medical applications. Communications in Nonlinear Science and Numerical Simulation, 2015, 24(1–3): 98-116. DOI:10.1016/j.cnsns.2014.12.005 |
| [8] |
Liao XF, Lai SY, Zhou Q. A novel image encryption Algorithm based on self-adaptive wave transmission. Signal Processing, 2010, 90(9): 2714-2722. DOI:10.1016/j.sigpro.2010.03.022 |
| [9] |
Wang XY, Zhang HL. A novel image encryption algorithm based on genetic recombination and Hyper-chaotic systems. Nonlinear Dynamics, 2016, 83(1–2): 333-346. DOI:10.1007/s11071-015-2330-8 |
| [10] |
王帅, 孙伟, 郭一楠, 等. 一种多混沌快速图像加密算法的设计与分析. 计算机应用研究, 2015, 32(2): 512-516. DOI:10.3969/j.issn.1001-3695.2015.02.042 |
| [11] |
米曾真, 朱革, 张红民, 等. 基于复合混沌模型的高级加密标准图像加密算法. 计量学报, 2016, 37(2): 138-142. DOI:10.3969/j.issn.1000-1158.2016.02.06 |
| [12] |
Wang Z, Huang X, Li YX, et al. A new image encryption algorithm based on the fractional-order hyperchaotic Lorenz system. Chinese Physics B, 2013, 22(1): 010504. DOI:10.1088/1674-1056/22/1/010504 |
| [13] |
Zhou SH, Wang B, Zheng XD, et al. An image encryption scheme based on DNA computing and cellular automata. Discrete Dynamics in Nature and Society, 2016, 2016: 5408529. |
| [14] |
田海江, 雷鹏, 王永. 基于混沌和DNA动态编码的图像加密算法. 吉林大学学报(工学版), 2014, 44(3): 801-806. |
| [15] |
Taneja N, Raman B, Gupta I. Chaos based cryptosystem for still visual data. Multimedia Tools and Applications, 2012, 61(2): 281-298. DOI:10.1007/s11042-011-0837-7 |
| [16] |
Deng XH, Liao CL, Zhu CX, et al. Image encryption algorithms based on chaos through dual scrambling of pixel position and bit. Journal of Communication, 2014, 35(3): 216-223. |
 2019, Vol. 28
2019, Vol. 28


