2. 解放军第107医院, 烟台 264001
2. 107th Hospital of the People’s Liberation Army, Yantai 264001, China
分布式拒绝服务攻击[1](Distributed Denial of Service, DDoS)是一种分布式、协作式、大规模的DoS攻击方式, 大多利用Internet上已被攻陷的计算机作为“僵尸”, 向某一特定的目标发起密集式的“拒绝服务”请求, 达到将其网络资源和系统资源耗尽的目的, 使之无法向真正正常请求的用户提供服务. Web服务器、DNS服务器多为最常见的攻击目标, 最终实现带有利益的恶意刷网站流量、Email 垃圾邮件群发、瘫痪竞争对手等违反道德的商业活动的目的. DDoS攻击作为互联网时代网络安全领域使用频率最高、最易实施和影响范围最广的网络攻击行为, 使军队、国家政府机关、企事业单位面临严峻的网络信息安全威胁和挑战.
国内外众多科研机构和人员针对DDoS攻防评估做了大量研究, 并取得了一定的成果, 文献[2]提出一种应对DDoS攻击防范机制的评估分类标准, 指出在评估一种防御机制中应用的一些标准参数, 但缺乏具体实验比较. 文献[3]提出DDoS防御机制评估框架, 但该方法需要一个严格假设才能清楚区分攻击包和合法包, 在实际的网络攻防对抗中难以做到. 文献[4]提出了一种基于多属性决策的DDoS防御策略遴选算法, 综合考虑了各方面评估指标, 为防御策略的选取提供了参考并通过模拟实验验证了方法的有效性. 文献[5]提出一种基于战略博弈的DDoS攻防绩效评估方法, 构建了基于博弈论的攻防策略模型, 定义攻防效用函数, 通过求解混合策略纳什均衡得到攻防最优策略. 上述评估方法仅从攻防结果中指标值变化或攻防行为收益的角度对DDoS防御策略进行评估较为片面, 属于静态评估, 缺乏对攻防过程的考虑并且得出最优防御措施缺乏针对性. 目前缺少一个综合考虑攻防对抗过程及结果的DDoS攻防行为评估方法.
本文的主要思想是综合考虑攻防对抗过程及结果, 从攻防行为强度和攻防收益两方面进行DDoS攻防行为评估, 首先基于随机Petri网理论建立DDoS攻防对抗网络, 然后对DDoS攻防对抗网络中的攻防行为进行攻防博弈分析, 得出攻防双方的攻防策略, 攻防策略即攻防行为选择概率, 将其赋予DDoS攻防对抗网展开攻防对抗过程, 依据攻防对抗网稳态概率对攻防行为进行评估.
2 基于随机Petri网的DDoS攻防行为对抗网本文基于随机Petri网针对DDoS攻防行为, 建立了攻防行为对抗网, 具体的有关随机Petri网的定义可参考文献[6].
2.1 相关定义定义1. 攻防收益
将攻击行为对系统造成的损害程度定义为攻击收益, 攻击行为i的收益表示为
定义2. 攻防策略
假设攻击方有n个攻击行为可供选择, 防御方有m个防御行为可供选择, 用
| $\begin{array}{l}{\pi ^{{a}}}{\rm{ = }}\left( {{\pi _1}^{{a}},{\pi _2}^{{a}}, \cdots ,{\pi _n}^{{a}}} \right){\pi _1}^{{a}}{\rm{ + }}{\pi _2}^{{a}}{\rm{ + }} \cdots {\rm{ + }}{\pi _n}^{{a}}{\rm{ = }}1\\{\pi ^d}{\rm{ = }}\left( {{\pi _1}^d,{\pi _2}^d, \cdots ,{\pi _n}^d} \right){\pi _1}^d{\rm{ + }}{\pi _2}^d{\rm{ + }} \cdots {\rm{ + }}{\pi _n}^d{\rm{ = }}1\end{array}$ |
定义3. 攻防行为强度
将单位时间内攻防行为产生或清洗攻击流量的能力视为攻防行为的强度, 用
定义4. DDoS攻防行为对抗网
用一个九元组来表示一个DDoS攻防行为对抗网,
(1) N={Na, Nd}, Na代表攻击方, Nd代表防御方;
(2)
(3) T=A
(4) F
(5)
(6)
(7) R: T
(8) S为标识集合, 常用S0表示ADSPN的初始状态.
2.2 DDoS攻防行为描述选取典型的DDoS攻防对抗行为作为构建DDoS攻防对抗网的行为集合.
2.2.1 攻击行为
(1) TCP连接洪水攻击
TCP连接洪水攻击是在TCP连接创建阶段对服务器资源进行攻击的. 攻击者可以利用大量受控主机, 通过快速建立大量恶意的TCP连接占满被攻击服务器的连接表, 使目标无法接受新的TCP连接请求, 从而达到拒绝服务攻击的目的.
(2) SYN洪水攻击[7]
SYN洪水攻击是最经典的一种拒绝服务攻击方式, 攻击者利用大受控主机发送大量的TCP SYN报文, 使服务器打开大量的半开连接, 占满服务器的连接表, 从而影响正常用户与服务器建立会话, 造成拒绝服务.
(3) Sockstress攻击
Sockstress攻击是一种慢速攻击TCP连接的方法. 在TCP传输数据时, 先将数据包临时存储在接收缓冲区中, 该缓冲区的大小是由TCP窗口表示的. 如果TCP窗口大小为0, 则表示该缓冲区已被填满, 发送端停止发送数据, 直到接收端窗口发生更新. Sockstress攻击就是利用该原理长时间维持TCP连接, 以达到拒绝服务攻击的目的.
2.2.2 防御行为
对DDoS攻击的治理就是对攻击源节点的治理, 发现并阻断DDoS攻击的源节点, 能够从源头停止正在进行的DDoS攻击.
(2) 攻击的缓解[10]
缓解DDoS攻击的主要方法是对网络流行清洗, 即设法将恶意的网络流量从全部流量中去除, 只将正常的网络流量交付给服务器.
2.3 DDoS攻防行为对抗网根据2.2节攻防行为描述, 我们首先构建攻击方攻击行为Petri网和防御方防御行为Petri网, 然后将攻击方和防御方的攻防行为Petri网进行组合, 构成DDoS攻防行为对抗网.
在图1中, 库所表示攻击方所处状态; 瞬间变迁表示攻击方对攻击行为的选择, 包含选择概率参数
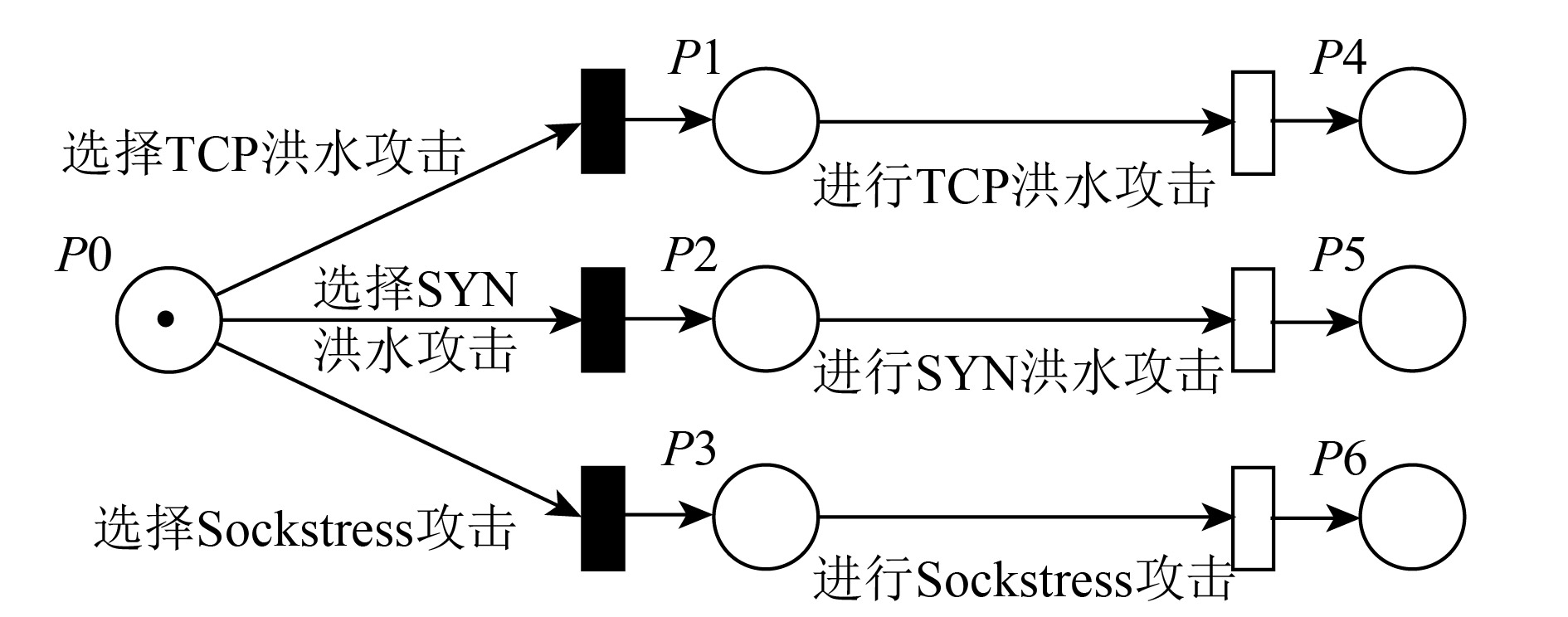
|
图 1 攻击行为Petri网 |
在图2中, 库所表示防御方所处状态; 瞬间变迁表示防御方对防御行为的选择, 包含选择概率参数

|
图 2 防御行为Petri网 |
攻击和防御是在网络攻防中是对立同一的整体, 二者相互依存. 在DDoS攻防对抗中, 攻击方首先进行攻击, 防御方检测到攻击后会采取防御行为抵御攻击, 然后攻击方会调整攻击策略再次攻击, 防御方也会调整策略进行防御, 这就形成一个循环的攻防对抗过程. 我们依据这个过程将攻击方和防御方的攻防行为Petri网进行组合, 构成DDoS攻防行为对抗网, 如图3所示.
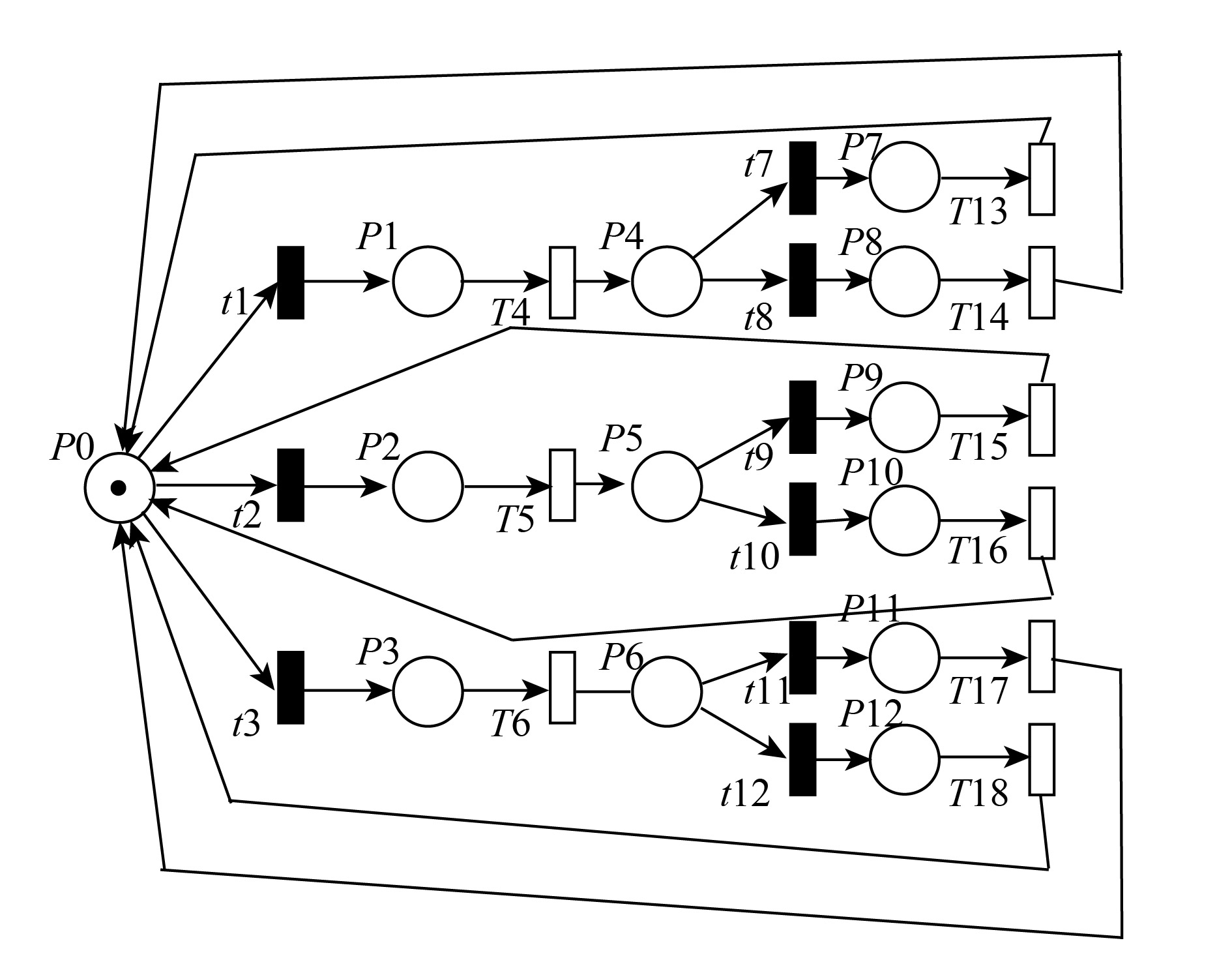
|
图 3 DDoS攻防对抗网 |
在DDoS攻防对抗网中, 我们以攻击方准备发动攻击作为初始状态, 攻击方发动攻击, 防御方对攻击行为展开防御使得攻击失效, 攻击方会再次发动攻击, 攻防对抗循环进行, 最终攻防对抗网会达到一个稳定状态, 即攻防双方会处于某个攻防状态的稳定概率, 我们依此来对攻防行为进行评估.
| 表 1 DDoS攻防对抗网库所含义 |
| 表 2 DDoS攻防对抗网变迁含义 |
3 基于攻防博弈的DDoS攻防策略求解方法
对于DDoS攻防对抗网, 攻防博弈的双方为攻击方和防御方, 在攻防博弈过程中, 攻防双方作为理性的局中人均以最大化自身收益作为选择攻防行为的准则, 一方的收益是在另一方的损失下得到的, 因此我们用零和博弈来描述攻击方和防御方两个局中人的博弈关系, 将防御方看做是与攻击方收益相反的局中人.
定义5. 攻防效用函数
用
| $\begin{array}{l}{U^{{a}}}({a_i},{b_j}) = R_{{i}}^{{a}} - R_{{j}}^{{b}}\\{U^{{d}}}({b_j},{a_i}) = R_j^b - R_i^a\end{array}$ |
定义6. 攻防策略纳什均衡
假设
| $E\left( {{\pi ^{{a}}},{\pi ^{{d}}}} \right){\rm{ = }}\sum\limits_{\forall {{{a}}_{{i}}} \in A} {\sum\limits_{\forall {{{d}}_{{i}}} \in D} {{\pi _i}^{{a}}{\pi _j}^{{d}}{U^a}\left( {{a_i},{d_i}} \right)} } $ |
那么攻防策略纳什均衡应满足以下两个条件:
(1)
(2)
当攻防博弈达到纳什均衡时, 双方所选择的策略都是应对对方的最优策略, 攻防双方所获得的收益都是最大的, 任何一方都不会主动降低自身收益去改变策略. 假设攻防博弈双方都是理性的局中人, 它们均要最大化自己的效用. 攻防双方零和博弈纳什均衡策略具体求解步骤如下:
(1) 输入攻防双方所有攻防行为收益:
| $R_1^{{a}},R_2^{{a}}, \cdots ,R_{{n}}^{{a}}$ |
| $R_1^d,R_2^d, \cdots ,R_{{m}}^d$ |
(2) 根据攻防行为收益函数
| ${\bf B}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}{\left( {{U^{{a}}}({a_1},{b_1}),{U^{{d}}}({b_1},{a_1})} \right)} & {\left( {{U^{{a}}}({a_1},{b_2}),{U^{{d}}}({b_2},{a_1})} \right)} & \cdots & {\left( {{U^{{a}}}({a_1},{b_{{m}}}),{U^{{d}}}({b_{{m}}},{a_1})} \right)}\\{\left( {{U^{{a}}}({a_2},{b_1}),{U^{{d}}}({b_1},{a_2})} \right)} & {\left( {{U^{{a}}}({a_2},{b_2}),{U^{{d}}}({b_2},{a_2})} \right)} & \cdots & {\left( {{U^{{a}}}({a_2},{b_{{m}}}),{U^{{d}}}({b_{{m}}},{a_2})} \right)}\\ \vdots & \vdots & {} & \vdots \\{\left( {{U^{{a}}}({a_{{n}}},{b_1}),{U^{{d}}}({b_1},{a_{{n}}})} \right)} & {\left( {{U^{{a}}}({a_{{n}}},{b_2}),{U^{{d}}}({b_2},{a_{{n}}})} \right)} & \cdots & {\left( {{U^{{a}}}({a_{{n}}},{b_{{m}}}),{U^{{d}}}({b_{{m}}},{a_{{n}}})} \right)}\end{array}} \right]$ |
(3) 将得到的攻防行为博弈矩阵输入Gambit软件中, 利用Gambit软件中Qre工具计算攻防策略纳什均衡.
(4) 输出DDoS攻防对抗行为攻防策略纳什均衡
上述步骤求得的攻防策略将会给DDoS攻防对抗网中瞬时变迁选择概率的设置提供依据.
4 稳态分析与仿真评估 4.1 稳态分析文献[11]已经证明, 一个随机Petri网同构于一个连续时间马尔科夫链, 所以本文所建立的DDoS攻防对抗网也同构于一个连续时间马尔可夫链(MC), 将DDoS攻防对抗网在随机Petri网仿真软件PIPE上进行仿真, 得到与之同构的马尔可夫链如图4所示.

|
图 4 同构的马尔可夫链 |
在图4中, S0、S4、S5、S6为消失状态, 因为它们所关联的库所触发瞬间变迁, 不存在稳态概率; S1、S2、S3、S7 、S8、S9、S10 、S11、S12为有形状态, 存在稳态概率. 其中, S3表示攻击方处于TCP连接洪水攻击状态、S2表示攻击方处于SYN洪水攻击状态、S1表示攻击方处于Sockstress攻击状态; S12表示防御方处于对TCP连接洪水攻击源进行阻断状态、S11表示防御方处于对TCP连接洪水攻击流量清洗状态、S9表示防御方处于备对SYN洪水攻击源进行阻断状态、S10表示防御方处于对SYN洪水攻击流量清洗状态、S8表示防御方处于对Sockstress攻击源进行阻断状态、S7表示防御方处于对Sockstress攻击流量清洗状态. 根据同构马尔可夫链中有形状态之间的转换关系, 我们可以得到稳定状态的可达标识集, 如表3所示.
| 表 3 可达标识集 |
4.2 仿真评估
首先我们只考虑攻防行为收益, 根据攻防效用函数建立攻防博弈矩阵, 如表4所示.
| 表 4 攻防博弈矩阵 |
根据攻防博弈矩阵使用软件Gambit使用软件计算攻防策略纳什均衡, 图5描述了计算攻防策略纳什均衡的过程.

|
图 5 攻防策略纳什均衡计算结果 |
由图5可知, 最终收敛的值即为攻防策略纳什均衡, 计算结果为:
| ${\pi ^a}^ * = (0.0612,0.2180,0.7278)$ |
| ${\pi ^{b * }} = (0.3333,0.6667)$ |
由此可知, 攻击方为了最大化自身收益, 最有可能采取Sockstress攻击, 而对防御方而言, 针对各类DDoS攻击最优的防御措施是对攻击流量进行清洗.
然后我们综合考虑攻防行为强度和攻防行为收益, 将攻防博弈求解纳什均衡得到攻防行为策略赋予DDoS攻防对抗网, 作为瞬间变迁选择执行概率参数
对DDoS攻防对抗网变迁参数设置如表5所示, 使用随机petri网建模软件PIPE对DDoS攻防对抗网进行仿真, 进行稳态概率求解, 最终求得稳态概率:
| $\begin{array}{l}p\left( {{S3}} \right) = 0.0545;p\left( {{S2}} \right) = 0.09706;p\left( {{S1}} \right) = 0.06481\\p\left( {{S{12}}} \right) = 0.00908;p\left( {{S{11}}} \right) = 0.06481\\p\left( {{S9}} \right) = 0.03235;p\left( {{S{10}}} \right) = 0.12943\\p\left( {{S8}} \right) = 0.32405;p\left( {{S7}} \right) = 0.21605\end{array}$ |
| ${\pi _{{{t}}1}}{\rm{ = }}\frac{{p\left( {{S3}} \right)}}{{p\left( {{S3}} \right){\rm{ + }}p\left( {{S2}} \right){\rm{ + }}p\left( {{S1}} \right)}}$ |
| ${\pi _{{{t2}}}}{\rm{ = }}\frac{{p\left( {{S2}} \right)}}{{p\left( {{S3}} \right){\rm{ + }}p\left( {{S2}} \right){\rm{ + }}p\left( {{S1}} \right)}}$ |
| ${\pi _{{{t3}}}}{\rm{ = }}\frac{{p\left( {{S1}} \right)}}{{p\left( {{S3}} \right){\rm{ + }}p\left( {{S2}} \right){\rm{ + }}p\left( {{S1}} \right)}}$ |
| ${\pi _{{{t7}}}}{\rm{ = }}\frac{{p\left( {{S{12}}} \right)}}{{p\left( {{S{12}}} \right){\rm{ + }}p\left( {{S{11}}} \right)}}$ |
| ${\pi _{{{t8}}}}{\rm{ = }}\frac{{p\left( {{S{11}}} \right)}}{{p\left( {{S{12}}} \right){\rm{ + }}p\left( {{S{11}}} \right)}}$ |
| ${\pi _{{{t9}}}}{\rm{ = }}\frac{{p\left( {{S9}} \right)}}{{p\left( {{S9}} \right){\rm{ + }}p\left( {{S{10}}} \right)}}$ |
| ${\pi _{{{t10}}}}{\rm{ = }}\frac{{p\left( {{S{10}}} \right)}}{{p\left( {{S9}} \right){\rm{ + }}p\left( {{S{10}}} \right)}}$ |
| ${\pi _{{{t11}}}}{\rm{ = }}\frac{{p\left( {{S8}} \right)}}{{p\left( {{S8}} \right){\rm{ + }}p\left( {{S7}} \right)}}$ |
| ${\pi _{{{t12}}}}{\rm{ = }}\frac{{p\left( {{S{10}}} \right)}}{{p\left( {{S9}} \right){\rm{ + }}p\left( {{S{10}}} \right)}}$ |
| 表 5 DDoS攻防对抗网参数设置 |
我们用以上公式对上述攻防双方所处攻防状态的概率进行处理, 使得结果更加清晰, 得到:
攻击方攻击状态概率
| ${\pi ^{a'}} = (0.2519,0.4486,0.2995)$ |
防御方针对三种攻击的防御状态概率
| ${\pi ^{d'}} = (0.1111,0.8889)$ |
| ${\pi ^{d''}} = (0.2000,0.8000)$ |
| ${\pi ^{d'''}} = (0.6000,0.4000)$ |
由此可知, 对于攻击方而言, 攻击方最可能处于SYN洪水攻击状态, 即最可能发动SYN洪水攻击; 而对防御方而言, 针对于洪水攻击, 防御方最可能采取攻击流量清洗措施, 针对于慢速攻击而言防御方最可能采取阻断攻击源措施抵御DDoS攻击.
参考文献[5,12]中针对基于博弈的DDoS攻防对抗评估方法, 只考虑攻防收益, 通过建立攻防博弈矩阵求得到DDoS攻防对抗评估结果为:
| ${\pi ^a}^ * = (0.0612,0.2180,0.7278)$ |
| ${\pi ^{d * }} = (0.3333,0.6667)$ |
将本文得到DDoS攻防对抗评估结果与用文献[5,12]方法得到的结果进行对比可以看出, 运用博弈论和随机Petri网思想综合考虑攻防行为强度和攻防行为收益评估出最优攻击行为是SYN洪水攻击, 同时攻击行为概率相差较小, 表明评估结果更加贴近实际, 并且防御行为评估具有针对性, 对于不同攻击行为, 本文方法能评估得出针对其最有效的防御行为.
5 结束语本文基于随机Petri网建立了DDoS攻防对抗网, 基于博弈论思想进行攻防博弈, 得出攻防行为策略并赋予攻防对抗网, 综合考虑攻防行为收益和攻防行为强度两方面针对DDoS攻防行为进行攻防对抗并评估, 得出的评估结果比只运用博弈论思想考虑攻防行为收益得到的评估结果更加合理且具有针对性. 本文的研究成果可运用于攻击行为的预测和防御策略的主动选取并提前部署.
下步工作就是结合评估结果对实际DDoS攻防对抗实验进行验证, 通过实际验证结果对本文所建立的攻防对抗网参数进行优化, 使其更具准确性和通用性.
| [1] |
鲍旭华, 洪海, 曹志华. 破坏之王: DDoS攻击与防范深度剖析. 北京: 机械工业出版社, 2014.
|
| [2] |
Mölsä JVE. A taxonomy of criteria for evaluating defence mechanisms against flooding DoS attacks. Blyth A. EC2ND 2005. London: Springer, 2006. 13–22.
|
| [3] |
Meadows C. A cost-based framework for analysis of denial of service in networks. Journal of Computer Security, 2001, 9(1-2): 143-164. DOI:10.3233/JCS-2001-91-206 |
| [4] |
黄亮, 冯登国, 连一峰, 等. 一种基于多属性决策的DDoS防护措施遴选方法. 软件学报, 2015, 26(7): 1742-1756. DOI:10.13328/j.cnki.jos.004673 |
| [5] |
石盼, 连一峰. 基于战略博弈的DDoS攻防绩效评估方法. 计算机工程, 2009, 35(3): 195-198. DOI:10.3969/j.issn.1000-3428.2009.03.066 |
| [6] |
林闯. 随机Petri网和系统性能评价. 北京: 清华大学出版社, 2000.
|
| [7] |
Jalan R, Kamat G, Szeto RWL. Mitigating TCP SYN DDoS attacks using TCP reset. US, 20180034848. [2018-02-01].
|
| [8] |
庄建儿. 浅析网络DDoS攻击与治理. 通讯世界, 2015(1): 33-34. DOI:10.3969/j.issn.1006-4222.2015.01.021 |
| [9] |
何亨, 胡艳, 郑良汉, 等. 云环境中基于SDN的高效DDoS攻击检测与防御方案. 通信学报, 2018, 39(4): 2018068. |
| [10] |
刘航, 曹建新, 张新建. 流量清洗系统在防御DDoS攻击中的应用. 科技信息, 2010(20): 249. DOI:10.3969/j.issn.1673-1328.2010.20.251 |
| [11] |
German R, Kelling C, Zimmermann A, et al. TimeNET-a toolkit for evaluating non-Markovian stochastic Petri nets. Proceedings of the 6th International Workshop on Petri Nets and Performance Models. Durham, NC, USA. 1995. 210-211.
|
| [12] |
张尚韬. 基于不完全信息静态博弈的DDoS防御机制评估方法研究. 佛山科学技术学院学报(自然科学版), 2017, 35(6): 12-16. |
 2019, Vol. 28
2019, Vol. 28


