协同过滤(Collaborative Filtering)是许多推荐系统常用的方法^[1]. 传统的基于协同过滤的方法使用用户给出的项目评分作为学习推荐的唯一信息来源. 但是, 许多应用程序的评分通常较少, 导致基于协同过滤的方法的推荐性能显着降低. 为了解决这个稀疏性问题, 本文利用诸如项目内容信息的辅助信息一同作为信息来源提出了称为协同深度学习(Collaborative In Deep Learning, CIDL)的算法, 该算法分别执行用于内容信息的深度表示学习以及用于评价(反馈)矩阵的协同过滤.

本文将协同深度学习算法应用于电影推荐系统, 对大量的电影评分进行建模, 分析观影用户对电影的偏好随着时间的推移而变化的情况, 从而对客户进行个性化电影推荐^[2]. 本文的创新点主要在于: (1) 与以往使用分类^[3]和重构^[4]等简单目标的深度学习模型不同, 本文在概率框架中使用协同过滤作为更复杂的目标. (2) 除了获得最大后验概率(Maximum A Posteriori, MAP)估计的算法外, 本文还推导了一种基于采样的CIDL贝叶斯处理算法, 该算法是一种贝叶斯推广的反向传播算法. (3) 协同深度学习是一个用于弥合现有深度学习模型和推荐系统之间差距的等级贝叶斯模型. 此外, 由于其贝叶斯性质, CIDL可以轻松扩展并纳入其他辅助信息以进一步提升性能.

1 相关工作

由于许多在线服务中用户有大量的选择, 推荐系统得到了大量运用^[5]. 对于个人而言, 使用推荐系统可以让我们更有效地使用信息. 此外, 许多公司(例如淘宝和各大音乐播放器)已经广泛地使用推荐系统来定位他们的客户. 推荐系统的现有方法大致可以分三类^[6]: 基于内容的方法, 基于协同过滤的方法和混合方法. 基于内容的方法利用用户程序或产品描述来进行推荐

基于协同过滤的方法使用过去的活动或偏好, 例如用户对项目的评分, 而不使用用户或产品内容信息. 混合方法通过结合基于内容的方法和基于协同过滤的方法来获得两全其美的结果.

根据判断评分信息与辅助信息之间是否存在双向交互, 可以进一步将混合方法分为两类: 松耦合方法和紧密耦合方法. 松散耦合的方法^[7]一次处理辅助信息, 然后用它为协同过滤模型提供特征. 由于信息流是单向的, 因此评级信息无法提供反馈来指导提取有用的功能. 对于这个子类别, 改进通常需要依靠手动和乏味的特征工程过程. 相反, 紧密耦合的方法允许双向交互^[8]. 一方面, 评分信息可以指导特征的学习. 另一方面, 提取的特征可以进一步提高协同过滤模型的预测能力. 通过双向交互, 紧密耦合的方法可以自动从辅助信息中学习特征, 并自然平衡评级和辅助信息的影响.

随着深度学习以及推荐系统的发展, 对于深度学习与推荐系统结合的研究也越来越多, 文献[9]选用了与本文相同的SDAE模型从用户自由文本标签中抽取项目的显式特征信息, 再使用改进隐因子模型算法对进行矩阵分解, 最终得出推荐矩阵, 但对于数据陷入局部最优的问题没有很好的解决. 文献[10]中使用结合协同过滤推荐和基于内容推荐的混合模型,其中基于内容推荐的部分使用了深度学习内容. 但对于这种方法而言, 是将两种算法产生的结果按比例返回作为推荐结果. 两种算法没有很好的融合在一起共同作用. 按比例返回结果的比例也很难把控. 文献[11]使用了两个堆叠降噪编码器来学习以得出推荐矩阵, 但预处理数据和训练模型时花费了较长的时间,最优效果有待改进. 文献[12]引入深度学习模型提升算法性能,但对于算法的调参提出了更高的要求,并且算法的复杂度也相比传统算法提升不少.

本文介绍了一种称为协同深度学习模型(Collaborative In Deep Learning, CIDL)的分层贝叶斯模型, 作为推荐系统的一种新型紧耦合方法. 协同深度学习模型基于一种称为堆叠降噪自动编码器(Stacked Denoising AutoEncoder, SDAE)的贝叶斯公式^[13]. 协同深度学习模型将内容信息的深度表示学习与评级(反馈)矩阵的协作过滤紧密结合在一起, 从而允许两者之间的双向交互.

2 本文算法 2.1 符号及公式说明

本文采用隐式反馈来训练和测试数据. 整个项目数据J(电影)的数据集合由一个j行S列的矩阵X_C来表示, J项目中的j行是由基于词汇库大小为S的词袋模型向量X_{C, j*}组成的. 对于整个用户数据集合I, 定义一个i行j列的二元评分矩阵R=R_{i, j}. 给定R中的部分评级和内容信息X_C, 用来预测R中的其他评级, R的维度为K. X₀为噪声破坏输入, 同样是一个j行S列的矩阵, X_C的作用为净化输入到SDAE中的X₀. X_l为SDAE的第l层的输出, X_l的j行表示为X_{l, j*}. W_l为l层的权重矩阵, b_l为偏差矢量. W⁺表示所有层的权重矩阵和偏差矢量的集合.

2.2 算法流程

本文使用自动编码器学习数据并得到训练后的网络, 在利用训练后的网络生成用户和项目间的隐含特征矩阵. 最后将该矩阵输入CIDL算法中训练学习, 最终得到新的评分矩阵. 流程图1所示.

图1 中的具体步骤如下:

(1)对数据进行预处理

本文中使用的数据由两部分组成. 第一部分, 收视率和电影名称来自Netflix挑战数据集. 第二部分, 本文从IMDB (http://www.imdb.com)收集了相应电影的情节. 为了与前两个数据集的隐式反馈设置保持一致^[14], 本文中只提取正面评分(评分5)进行培训和测试. 在移除正面评级少于3个的用户和没有剧情的电影后, 最终数据集中有407 261个用户, 9228部电影和15 348 808个评分. 之后进行预处理^[15], 从电影的情节中提取文本信息(项目内容). 在去除停止词后, 根据tf-idf(term frequency–inverse document frequency)值选择最高的S个判别式词汇形成词汇表, 最后生成的词汇表大小为20 000.

(2)训练SDAE自动编码器输出特征矩阵

对自动编码器中的每个用户输入R里的每一行、项目ID和项目特征向量, R里的每一行即每个用户对各个项目的打分作为其向量描述,输入层个数等于项目数目J. 对于R加噪后的数据为:

${\tilde R^{\left( {{u}} \right)}}{\rm{ = }}\left( {{{\tilde R}_{{{u1}}}}, \cdots ,{{\tilde R}_{{{um}}}}} \right) \in {\tilde R^{{n}}}$

(1)

训练用户评分矩阵的自动编码器的输出公式为:

${\hat R^{\left( {{u}} \right)}}{{ = f}}\left( {W{'_1}g\left( {{W_1}{{\tilde R}^{\left( u \right)}} + {b_1}} \right) + b{'_1}} \right) $

(2)

其中, W, W'分别是训练用户评分矩阵的自动编码器中输入层到隐藏层、隐藏层到输出层的权重矩阵, b, b'分别是偏置向量. 对于训练用户评分矩阵的自动编码器的最小损失函数为:

${E_U} = \frac{1}{{2m}}\sum\limits_{u = 1}^m \parallel {R^{(u)}} - {\hat R^{(u)}}{\parallel ^2} + \frac{\lambda }{2}\parallel {W_1}{\parallel ^2} + \frac{\lambda }{2}\parallel W{'_1}{\parallel ^2}$

(3)

(3)使用CIDL算法生成新的评分矩阵

生成的具体过程如2.5小节所示.

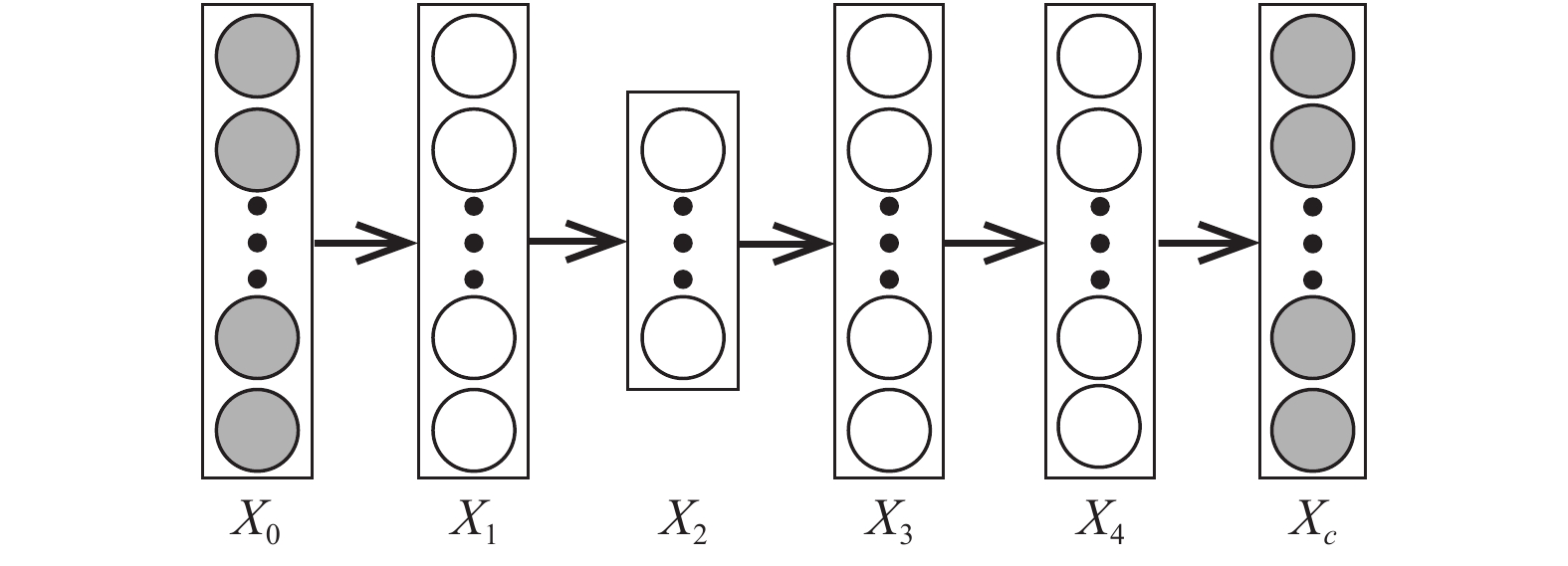
2.3 堆叠降噪自动编码器

堆叠降噪自动编码器是一个前馈神经网络, 通过从叠加噪声的原始数据以及输出数据中学习得出未叠加噪声的入数据, 如图2所示.

堆叠降噪自动编码器从叠加噪声的输入数据与未叠加噪声的输入数据中得出的特征几乎相同, 但从叠加噪声的数据中学习到的特征更具有鲁棒性. 通常情况下, 隐藏层在整个系统的中间(即图1中的X₂)被约束为瓶颈^[15], 并且输入层X₀是叠加噪声的原始数据. 一个堆叠降噪编码器解决了去除噪声的优化问题, 即:

$\mathop {\min }\limits_{{\rm{\{ }}{W_l}{\rm{\} ,\{ }}{b_l}{\rm{\} }}} \parallel {X_c} - {X_L}\parallel _F^2 + \lambda \sum\limits_l {\parallel {W_l}\parallel _F^2} $

(4)

其中, λ是正则化参数, ||·||是弗罗贝尼乌斯范数.

2.4 广义贝叶斯SDAE

从X_L生成干净输入X_C是贝叶斯SDAE生成过程的一部分, 而从X_C生成噪声破坏输入X₀是一种人工噪声注入过程, 可帮助SDAE学习更强大的特征表示. 若假设干净输入X_C和损坏输入X₀, 可定义以下生成过程:

(1)对于SDAE网络中的每一层l

1)对于权重矩阵NW_l的每一列n

${W_{l,*n}} \sim {\cal{N}}(0,\lambda _W^{ - 1}{I_{{K_l}}}) $

(5)

2)绘制偏向量

${b_l} \sim {\cal{N}}(0,\lambda _{{W}}^{ - 1}{I_{{K_l}}}) $

(6)

3)对于X_l的每一行j

${X_{l,j*}} \sim {\cal{N}}(\delta ({X_{l - 1,j*}},{W_i} + {b_l}),\lambda _{{S}}^{ - 1}{I_{{K_l}}}) $

(7)

(2)对于每个j, 绘制一个干净的输入

${X_{C,j*}} \sim {\cal{N}}({X_{L,j*}},\lambda _n^{ - 1}{I_J}) $

(8)

如果λ_S有效, 则方程(4)中的高斯分布将变为以δ(X_{l-1, j*}, W_i+b_l)为中心的狄拉克三角形分布^[10], 其中δ(*)是S形函数(Sigmoid Function, SF). 该模型将退化为SDAE的贝叶斯公式, 因此称之为广义SDAE. 网络中的第一个L/2层充当编码器, 最后的L/2层充当解码器. 后验概率的最大化等同于考虑权重衰减时重建误差的最小化.

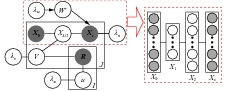
2.5 协同深度学习

使用贝叶斯SDAE作为组件, CIDL的原理图如图3所示.

CIDL的生成过程如下:

(1) 对于SDAE网络的每一层l, 操作与前一部分SDAE中步骤相同.

(2) 对于每个j, 绘制一个干净的输入, 操作与SDAE中步骤相同.

1)设置一个潜在的项目设置向量:

${\varepsilon _j} \sim {\cal{N}}(0,\lambda _v^{ - 1}{I_K}) $

(9)

2)并将潜在项目矢量设置为:

${v_j} = {\varepsilon _j} + X_{\frac{L}{2},j*}^{\rm T} $

(10)

3)为每个用户设置一个潜在用户向量:

${u_i} \sim {\cal{N}}(0,\lambda _u^{ - 1}{I_K}) $

(11)

4)为每个用户项目对(i, j)绘制评分R_{i, j}:

${R_{i,j}} \sim {\cal{N}}(u_i^{\rm T}{v_j},C_{ij}^{ - 1}) $

(12)

其中, λ_W, λ_n, λ_u, λ_S以及λ_v为超参数, C_ij是一个与CTR相似的置信参数, 中间层作为评级和内容信息之间的桥梁. 这个中间层, 以及潜在偏移量ε_j是使CIDL能够同时学习有效特征表示并捕获项目与用户之间相似性和隐含关系的关键.

2.6 最大后验估计

基于上述CIDL模型, 所有参数都可以作为随机变量处理, 以便可以应用完全贝叶斯方法, 如马尔科夫链或变分近似方法^[16]. 但是, 这种处理通常会导致高计算成本. 本文设计了一个期望最大算法来进行最大后验估计.

与协同主题回归模型类似, 最大化后验概率相当于最大化U, V, {X_l}, {X_C}, {W_l}, {b_l}的联合对数似然估计:

$\begin{split}{\cal{L}} =& - \displaystyle\frac{{{\lambda _u}}}{2}\displaystyle\sum\limits_i {||{u_i}} ||_2^2 - \displaystyle\frac{{{\lambda _w}}}{2}\displaystyle\sum\limits_l {(||{W_l}||_F^2} + ||{b_l}||_2^2)\\& - \displaystyle\frac{{{\lambda _v}}}{2}\displaystyle\sum\limits_j {||{v_j} - X_{\frac{L}{2},j*}^{\rm T}} ||_2^2 - \displaystyle\frac{{{\lambda _n}}}{2}\displaystyle\sum\limits_j {||{X_{L,j*}} - {X_{c,j*}}} ||_2^2)\\& - \displaystyle\frac{{{\lambda _s}}}{2}\displaystyle\sum\limits_l {\displaystyle\sum\limits_j {||\delta ({X_{l - 1,j*}}{W_l} + {b_l}) - {X_{l,j*}}||_2^2} } \\& - \displaystyle\sum\limits_{i,j} {\displaystyle\frac{{{C_{i,j}}}}{2}} {({R_{ij}} - u_i^{\rm T}{v_j})^2}\end{split}$

(13)

若λ_S趋近于无限, 此似然将会变为:

$\begin{split}{\cal{L}}= &- \displaystyle\frac{{{\lambda _u}}}{2}\displaystyle\sum\limits_i {||{u_i}||_2^2} - \displaystyle\frac{{{\lambda _w}}}{2}\displaystyle\sum\limits_l {(||{W_l}} ||_F^2 + ||{b_l}||_2^2)\\& - \displaystyle\frac{{{\lambda _v}}}{2}\displaystyle\sum\limits_j {||{v_j} - {f_e}{{({X_{0,j*,}}{W^ + })}^{\rm T}}||_2^2} \\& - \displaystyle\frac{{{\lambda _n}}}{2}\displaystyle\sum\limits_j {||{f_r}} ({X_{0,j*,}}{W^ + }) - {X_{c,j*}}||_2^2\\& - \displaystyle\sum\limits_{i,j} {\displaystyle\frac{{{C_{ij}}}}{2}{{({R_{ij}} - u_i^{\rm{T}}{v_j})}^2}} \end{split}$

(14)

编码器函数fe(*, W+)取未降噪的的内容向量X_{0, j*}作为输入并计算该项的编码, 函数fr(*, W+)同样取X_0,j*作为输入并计算编码, 然后计算项目j的重构内容向量.

从优化的角度来看, 上述目标函数(11)中的第三项相当于一个多层感知器, 它使用潜在项向量v_j作为目标, 而第四项等价于一个使重建误差最小化的SDAE. 从神经网络的角度来看, 当λ_S接近正无穷时, CIDL的概率图模型的训练将退化为同时训练两个叠加在一起的共同输入层的神经网络. 由于参与评级矩阵, CIDL网络比典型的神经网络复杂得多.

当λ_n/λ_v的比率接近正无穷时, CIDL将退化为两步模型, 其中使用SDAE学习的潜在表示被直接放入协同主题回归模型中. 另一个临界点发生在λ_n/λ_v趋近于零时SDAE的解码器基本失去功能. 通过实验证实可得, 在这两种情况下, 模型预测性能都会大大提高.

对于u_i和v_j, 给定当前W+, 计算 ${\cal{L}}$ 相对于u_i和v_j的梯度并将它们设置为零, 得出以下结果:

${u_i} \leftarrow {{\rm{(}}V{C_i}{V^{\rm T}}{\rm{ + }}{\lambda _u}{I_k}{\rm{)}}^{{\rm{ - 1}}}}V{C_i}{R_i}$

(15)

${v_j} \leftarrow {(U{C_i}{U^{\rm T}} + {\lambda _v}{I_K})^{ - 1}}(U{C_j}{R_j} + {\lambda _v}{f_e}{({{{X}}_{0, j*}}, {{{W}}^ + })^{\rm T}})$

(16)

其中, $U{\rm{ = (}}{{{u}}_i}{\rm{)}}_{i{\rm{ = 1}}}^{{I}}{\rm{, }}V{\rm{ = (}}{{{v}}_j}{\rm{)}}_{j{\rm{ = 1}}}^{{J}}{\rm{, }}{C_i} = diag({C_{i1}}, \cdots , {C_{iJ}})$ 为对角矩阵, ${{{R}}_i} = {({{{R}}_{i1}}, \cdots , {{{R}}_{i, J}})^{\rm T}}$ 为包含用户所有评级的列向量.

对于给定U和V, 可以使用反向传播学习算法来学习权重W_l以及每个层的偏差矢量b_l. 关于W_l和b_l的可能性的梯度如下:

$\begin{split}\nabla {w_l}{\cal{L}} =& - {\lambda _w}{W_l}\\ &- {\lambda _v}\displaystyle\sum\limits_j {\nabla {w_l}{f_e}{{({X_{0,j*}},{W^ + })}^{\rm T}}({f_e}{{({X_{0,j*}},{W^ + })}^{\rm T}} - {v_j})} \\ &- {\lambda _n}\displaystyle\sum\limits_j {\nabla {w_l}{f_r}({X_{0,j*}},{W^ + })({f_r}({X_{0,j*}},{W^ + }) - {X_{c,j*}})} \end{split}$

(17)

$\begin{split}\nabla {b_l}{\cal{L}} = & - {\lambda _w}{b_l}\\& - {\lambda _v}\displaystyle\sum\limits_j {\nabla {b_l}{f_e}{{({X_{0,j*}},{W^ + })}^{\rm T}}({f_e}{{({X_{0,j*}},{W^ + })}^{\rm T}} - {v_j})} \\& - {\lambda _n}\displaystyle\sum\limits_j {\nabla {b_l}{f_r}({X_{0,j*}},{W^ + })({f_r}({X_{0,j*}},{W^ + }) - {X_{c,j*}})} \end{split}$

(18)

通过交替更新U, V, W_l和b_l, 可得到 ${\cal{L}}$ 的局部最优值. 本文使用SGD ( Stochastic Gradient Descent, 随机梯度下降) ^[17] 算法也叫增量梯度下降法, 是在传统梯度下降法的基础上改进而来,收敛速度快很多, 是常用的参数训练算法. SGD 通过最小化损失函数来训练模型参数, 根据每个样本来迭代更新一次, 可以控制下降速率和迭代次数, 使得参数的训练更可控,以解决局部最优问题. 该算法过程如算法1.

算法1. 增量梯度下降法

Input: 评分矩阵 R, 特征向量维度K, 学习率 η, 比例参数α, 正则参数λ_U,λ_V,λ_Q

Output: U, V

(1) 初始化: 用一个较小的值随机构造U, V 和 $\scriptstyle Q$ ;

(2) while (error on validation set decrease);

(3) $\scriptstyle {\nabla _{U{\cal{L}}}} = I\left( {{U^{\rm T}}V - R} \right)V + \alpha \left( {{U^{\rm T}}Q - H} \right)Q + {\lambda _U}U$

$\scriptstyle {\nabla _{V{\cal{L}}}} = {[I({U^{\rm T}}V - R)]^{\rm T}}U + {\lambda _V}V$

$\scriptstyle {\nabla _{Q{\cal{L}}}} = \alpha {({U^{\rm T}}Q - H)^{\rm T}}U + {\lambda _Q}Q$

(4) $\scriptstyle {\rm{set}}\;\eta = 0.1$

(5) $\begin{array}{*{20}{l}}\scriptstyle {{\rm{while}}{(_{\cal{L}}}(U - \eta {\nabla _{U{\cal{L}}}},V - \eta {\nabla _{V{\cal{L}}}}{\rm{ }},Q - \eta {\nabla _{Q{\cal{L}}}}){ > _{\cal{L}}}(U,V,Q){\rm{ }})}\end{array}$

(6) $\scriptstyle {\rm{set}}\;\eta = {\rm{ }}\eta/2$

(7) $\scriptstyle {\rm{End while}}$

(8) $\scriptstyle U = U - \eta {\nabla _{U{\cal{L}}}}$

$\scriptstyle V = V - \eta {\nabla _{V{\cal{L}}}}$

$\scriptstyle Q = Q - \eta {\nabla _{V{\cal{L}}}}$

(9) $\begin{array}{*{20}{l}}\scriptstyle {{\rm{End while}}} \end{array}$

(10) $\begin{array}{*{20}{l}}\scriptstyle {{\rm{Return}}\;U,V}\end{array}$

本文对SDAE模型进行了改进, 并与协同过滤模型进行结合, 最后使用增量梯度下降算法解决了局部最优化问题, 在数据处理与推荐准确性方面有了较大提升。

3 实验和分析 3.1 评估计划

在数据集中随机选择与每个用户相关的P项以形成训练集^[18], 并将所有剩余的数据集用作测试集. 为了在稀疏和密集设置下评估和比较模型, 本文在实验中分别将P设置为1和10. 对于P的每个值, 用不同的随机选择训练集重复评估五次, 并记录平均性能. 本文使用查全率作为性能度量, 由于评级信息采用隐式反馈的形式, 零条目可能是用户对该项目不感兴趣, 或者用户不知道其存在. 因此, 精度不是一个合适的性能指标. 像大多数推荐系统一样, 本文对候选项目的预测评级进行了排序^[19], 并向目标用户推荐前M项目. 每个用户的查全率@ M被定义为:

　　　　　 ${{@M = }}\displaystyle\frac{{\text{在}{{M}}\text{中用户喜欢的项目数}}}{\text{用户喜欢的项目总数}}$

最终结果是所有用户的平均查全率.

3.2 基线和实验设置

本文中将协同深度学习算法(CIDL)同时与CMF算法^[20]、SVDFeature算法^[21]、CTR算法^[8]以及DeepMusic^[22]算法应用中的各项指标进行比较. 在实验中, 本文首先使用一个验证集来寻找CMF、SVDFeature, CTR以及DeepMusic的最佳超参数. CMF算法中将不同上下文的潜在因子的正则化超参数设置为10. 在网格搜索之后, CMF在等级矩阵和内容矩阵的权重均为稀疏度为5. 密度设置中的权重分别为8和2. SVDFeature算法中, 用户和项目的正则化超参数为0.004且学习率等于0.005. DeepMusic算法中, 使用具有两个卷积层的CNN. CTR算法中, 使用的参数为λ_u = 0.1, λ_v = 10, a = 1, b = 0.01, K = 50.

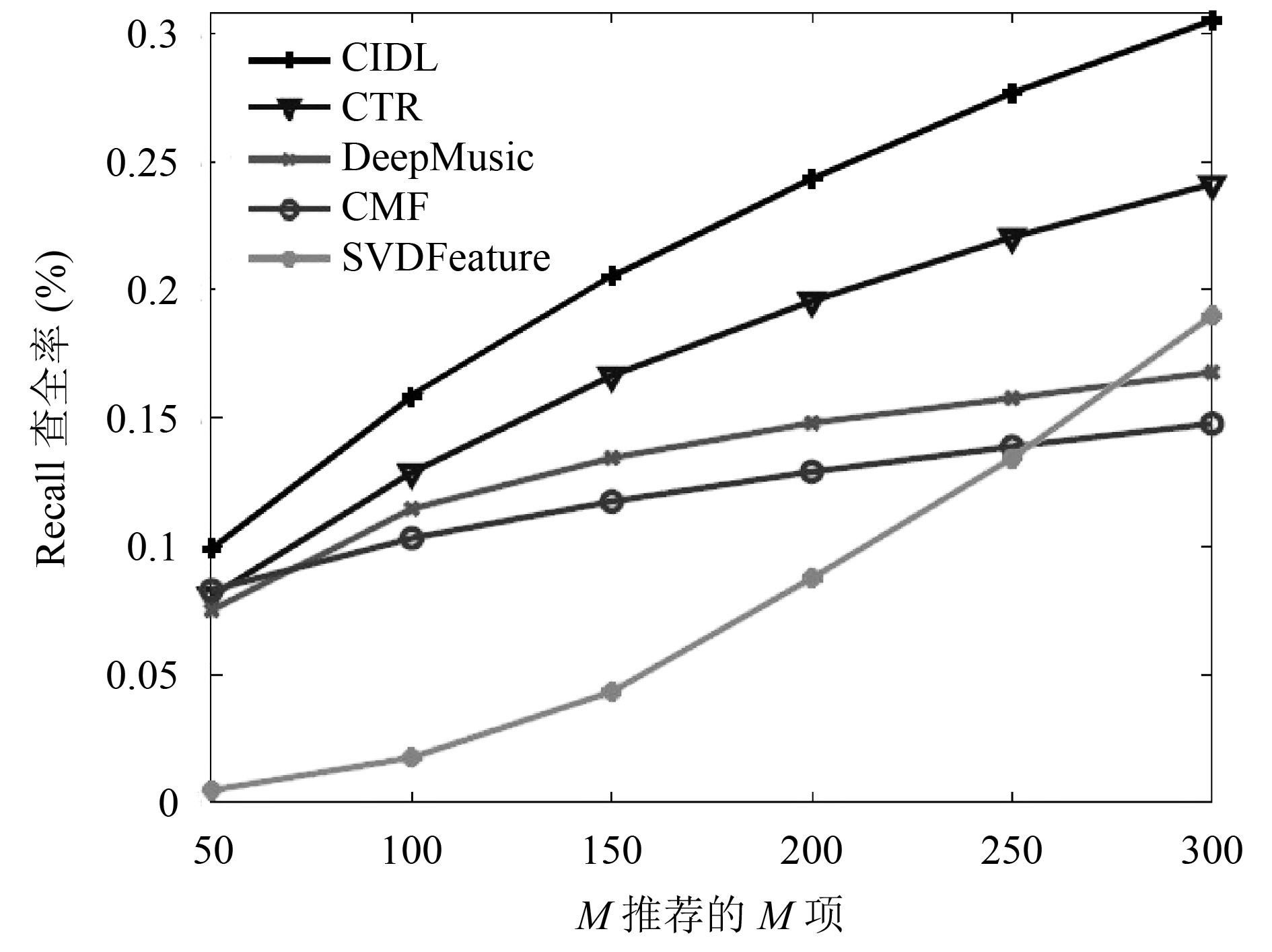
3.3 平均查全率分析

图4和图5显示了在稀疏(P = 1)和密集(P = 10)设置下使用电影数据集比较CIDL算法, CTR算法, DeepMusic算法, CMF算法以及SVDFeature算法的结果. 由图像可得, 无论在数据集密度稀疏还是密集, CIDL算法都优于其他四种算法. 在数据密集的情况下虽然DeepMusic算法具有优秀的体系结构, 但CTR算法在数据处理中更为优秀. 在稀疏设置中, CMF算法大部分时间都比SVDFeature算法优秀, 有时可以达到与CTR算法相当的性能. DeepMusic算法由于缺乏评分而表现不佳. 在密集的环境中, SVDFeature算法对于Netflix数据来说来说, 效果不如CMF. 在稀疏设置中2层CIDL的性能比CTR高出1.9%, 在密集设置下高出1.5%–2.0%. 由实验可以得出, 深度学习和推荐系统的整合算法是成功的, 对于查全率有显著的提升.

在稠密环境下使用不同Δn也有不同结果, 如图6所示.

当λ_n趋近于无限大时, λ_n/λ_v将会趋近正无穷, 此时CIDL将退化为两个单独的模型. 在这种情况下, SDAE将以无监督方式学习潜在项目表示, 然后将其直接放入CTR的简化版本中. 这种情况下, 贝叶斯SDAE和基于矩阵分解的协同过滤组件之间没有交互作用, 预测性能将大大提高. 对于另一个极端, 当λ_n无限小时, λ_n/λ_v将趋近于近零, 此时CIDL退化为贝叶斯SDAE分量解码器基本消失的情况. 此时贝叶斯SDAE组件基本消失, 编码器将通过简单矩阵分解学习潜在项目向量. 如图6所示, 预测性能随着λ_n变化而变化. 当λ_n<0.1时, 查全率@M已经非常接近PMF的结果(或甚至比PMF结果还要差).

综合以上实验结果, 在大量数据的实验证明下可知, 不论在数据密集或是数据稀疏的情况下CIDL算法都优于CMF算法、SVDFeature算法、DeepMusic算法、CTR算法以及DeepMusic算法. 而在CIDL算法中算法的预测性能会随着λn的变化而变化, 因此在CIDL算法中只有通过实验找到最合适的λn值, 才能更好的提高算法效率.

4 结束语

本文中展示了通过联合对内容信息的深度学习和对评级(反馈)矩阵进行协作性过滤从而实现出色的性能的算法. CIDL算法是一个用于弥合最先进的深度学习模型和推荐系统之间差距的等级贝叶斯模型. 在深度学习方面, 除了获得MAP估计的算法外, 本文还推导了一种基于采样的CIDL贝叶斯处理算法, 作为反向传播的贝叶斯广义版本.