柔性车间调度[1](Flexible Job-shop Scheduling Problem, FJSP)突破机器约束和加工过程路线固定的限制, 每道工序可在一台或多台机器上进行加工. 目前车间调度研究热点仍把最小最大完工时间作为主要指标, 这样会导致库存积压等情况, 但如果工件拖期完工会打乱生产节拍, 出现缺件等情况的发生, 任何提前或拖期(E/T)都会产生相应的惩罚成本. 因此柔性车间E/T调度相比于传统作车间调度更具有实际意义.
过去研究中, 科学家们尝试各种方法, 比如一些传统的确定性算法, 分值界定算法, 但是随着工件和机器数量的增加, 问题变得越来越复杂, 这些确定性算法无法满足问题的需求. 因此, 很多学者开始引入不确定性算法, 比如遗传算法, 粒子群算法等等. 刘爱军等[2]利用改进的多种群遗传算法解决柔性车间调度问题; 蔡霞等[3]提出基于浮点型编码策略的差分多目标进行柔性车间调度优化; 侯晓莉等[4]及马立波等[5]将粒子群算法引进柔性车间问题并求解; 薛宏全等[6]利用改进的蚁群算法求解柔性车间问题; 栾飞等[7]基于PST层次结构的改进GA求解柔性车间调度问题; 徐华等[8]利用新型离散蝙蝠算法求解柔性流水车间调度问题; 傅卫平等[9]利用改进的遗传算法求解柔性车间调度. 随着群智能发展, 出现一种模拟萤火虫发光求偶觅食行为的萤火虫算法[10](Glowworm Swarm Optimization, GSO). 目前, 利用GSO算法解决调度问题尚在探索阶段, 还未具体应用到柔性车间E/T调度问题中.
综上所述, GSO算法还未应用于柔性车间E/T调度问题中, 针对问题特点, 提出改进的GSO算法, 算法设计了一种具有贪婪思想的编码策略, 采用自适应选择策略, 使步长自适应, 提高算法精度; 引入POX交叉、邻域交换和反序排序方法提高算法局部和全局寻优能力, 并利用贪婪思想, 提高算法的收敛速度.
1 柔性作业车间E/T调度问题模型 1.1 问题描述柔性车间调度是传统作业车间调度的扩展, 在原有问题基础上, 增加机器资源可选择这一环节, 在加大了调度灵活性的同时, 也加大了求解难度. 柔性车间调度问题可以简单描述为在给定资源条件下, 合理安排工件加工顺序、分配机器, 完成工件加工任务. 具体描述如下:
n个工件在m台机器上进行加工, 每个工件有一道或多道工序, 每道工序可在不同机器进行加工, 但不同机器加工同一工序的时间不一样. 调度任务的目标: 首先确定加工每道工序的机器, 其次确定每个工件在每台机器上的加工顺序, 从而优化某些生产指标, 比如最普遍的性能指标为最小最大完工时间. 完工时间是指某个工件开始进入第一道工序到最后一道工序的完成时间, 所有工件的完成时间中最长的那个即位最大完工时间且使最大完工时间最小化.
1.2 模型假设假设1. 同一时刻, 一台机器只能加工一个工件, 即一个工件只能选择一台机器, 不可同时选择多台机器.
假设2. 同一时刻, 一个工件只能在一台机器上进行加工, 且不被间断.
假设3. 同一工件, 工序之间有先后顺序约束; 不同工件的工序之间没有先后顺序约束.
假设4. 每个工件的工序有特定加工顺序.
假设5. 每个工件的准备时间为0.
假设6. 不同工件具备相同的优先级, 即每个时刻, 每个都有可能被加工.
假设7. 加工过程中, 装载、卸载时间忽略不计.
1.3 变量及参数说明N: 表示工件总个数;
M: 表示机器总个数;
J={1, 2,…, j}: 表示需要加工的工件的集合;
K={1, 2,…, k}: 表示机器的集合;
Xijk: 表示工件j的工序i是否在机器k上进行加工, 取值为0或1;
tijk: 表示工件j的工序i在机器k上的需要加工的时间;
bijk: 表示工件j的工序i在机器k上的开始加工时间;
tj: 工件j的完工时间;
dj: 工件j的交货期;
rj: 工件j的提前惩罚系数;
wj: 工件j的拖期惩罚系数.
1.4 模型建立(1) 目标函数
| ${{\min T = \min}} \begin{array}{l}\left\{\sum\limits_{{{k = 1}}}^{{M}} {\sum\limits_{{{j = 1}}}^{{N}} {\sum\limits_{{{i = 1}}}^{{{{N}}_{{j}}}} {{{{t}}_{{{ijk}}}}} } } {{{x}}_{{{ijk}}}}{\rm{ + }}\sum\limits_{{{j = 1}}}^{{N}} {\left[ {{{{r}}_{{j}}}{{\max((}}{{{d}}_{{j}}}{\rm{ - }}{{{t}}_{{j}}}{{),0)}}} \right]}\right. \\\left.{{ + }}\sum\limits_{{{j = 1}}}^{{N}} {\left[ {{{{w}}_{{j}}}{{\max((}}{{{t}}_{{j}}}{{ - }}{{{d}}_{{j}}}{\rm{),0)}}} \right]} {\rm{ }}\right\}\end{array} $ | (1) |
(2) 约束条件
工序约束: 同一工件的工序之间有先后约束.
| $\sum\limits_{{{k = 1}}}^{{M}} {{{{b}}_{{{ijk}}}}{{{x}}_{{{ijk}}}}{\rm{ }} \geqslant {\rm{ }}\left[ {{\rm{(}}{{{b}}_{\rm{(}}}_{{{i - 1)jk}}}{\rm{ + }}{{{t}}_{\rm{(}}}_{{{i - 1)jk}}}{\rm{)}}} \right]} {{{x}}_{\rm{(}}}_{{{i - 1)jk}}}$ | (2) |
机器约束: 同一台机器在同一时刻只能加工一道工序.
| $\forall {{t,}}\;\exists {{{x}}_{{{ijk}}}} = 1,{\text{则 }}{{{x}}_{{{xym}}}} = 1{\text{必不成立}}\left( {{{j}} \ne {{y;i}} \ne {{x}}} \right)$ | (3) |
连续性约束: 工序在加工过程中不能中断.
| ${{{t'}}}{_{{ijk}}} = \left\{ \begin{array}{l}{{\max}}\left\{ {{{{t'}}}{{_{{i(j - 1)k}}}}, {{{b}}_{{{ijk}}}}{\rm{ }}} \right\}{\rm{ + }}{{{t}}_{{i}}}_{{{jk}}}, \;\;\;\;{{j > 1}}\\{{{b}}_{{{ijk}}}}{\rm{ + }}{{{t}}_{{{ijk}}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{j = 1}}\end{array} \right.$ | (4) |
工件约束: 同一时刻, 每个工件只能在一台机器上进行加工.
| $\sum\limits_{{{k = 1}}}^{{M}} {{{{x}}_{{{ijk}}}}{{ = 1,1}} \leqslant {{j}} \leqslant {{N,1}} \leqslant {{i}} \leqslant {{{N}}_{{j}}}{{,1}} \leqslant {{k}} \leqslant {{M}}} $ | (5) |
萤火虫算法作为一种模仿自然界中萤火虫的发光特性的随机优化算法, 在算法中舍弃了萤火虫其他的生物意义, 只利用其发光特性在其搜索领域寻找伙伴, 并向领域内位置较优的萤火虫伙伴移动, 从而实现位置的更新.
在该算法中, 萤火虫彼此吸引的原因主要取决于两个因素: 自身的亮度跟吸引度. 其中萤火虫的发光亮度取决于萤火虫当前所在的位置, 位置越好萤火虫的亮度越高, 即目标值越佳. 吸引度跟亮度有关, 亮度越高吸引力越大. 如果发光亮度相同, 则萤火虫会随机移动. 亮度与吸引度与萤火虫之间的距离成反比, 都随着距离的增加而减小.
(1) 荧光素的更新
萤火虫的荧光素大小的决定了萤火虫在搜索空间的位置, 此外荧光素的大小还与上一代迭代的萤火虫的荧光素挥发有关系, 如式(6)所示:
| ${{{l}}_{{i}}}(t) = \left( {1 - \rho } \right) * {l_i}(t - 1) + \gamma * f\left( {{x_i}\left( t \right)} \right)$ | (6) |
其中,
(2) 移动的概率计算
在这个阶段, 每个萤火虫根据自身的决策半径
| $\begin{array}{c}{{{p}}_{ij}}\left( t \right) = \displaystyle\frac{{{l_j}\left( t \right) - {l_i}\left( t \right)}}{{\sum\limits_{k \in {N_i}\left( t \right)} {{l_k}\left( t \right) - {l_i}\left( t \right)} }}\\{{j}} \in {N_{{i}}}\left( t \right),{N_{{i}}}\left( t \right) = \left\{ {j:\left\| {{x_j}\left( t \right) - {x_i}\left( t \right)} \right\| < r_d^i(t);{l_i}\left( t \right) < {l_j}\left( t \right)} \right\}\end{array}$ | (7) |
其中,
(3) 个体位置更新
经过上一步骤后, 从满足了集合Ni(t)的两个条件个体中选取了同伴个体j, 位置更新按照式(8)如下:
| ${{{x}}_{{i}}}\left( {{{t + 1}}} \right){\rm{ = }}{{{x}}_{{i}}}\left( {{t}} \right){{ + s*}}\left( {\frac{{{{{x}}_{{j}}}\left( {{t}} \right){\rm{ - }}{{{x}}_{{i}}}\left( {{t}} \right)}}{{\left\| {{{{x}}_{{j}}}\left( {{t}} \right){\rm{ - }}{{{x}}_{{i}}}\left( {{t}} \right)} \right\|}}} \right)$ | (8) |
其中, s表示的移动步长,
(4) 决策半径更新
位置更新以后, 根据移动后的位置周围邻居个数, 来更新个体的决策半径, 具体如式(9)所示:
| ${{r}}_d^i\left( {t + 1} \right) = \min \left\{ {{r_s},\max \left\{ {0,r_d^i\left( t \right) + \beta \left( {{n_t} - \left| {{N_i}(t)} \right|} \right)} \right\}} \right\}$ | (9) |
其中, rs表示个体的最大决策半径, nt调整萤火虫邻域集合大小的参数,
为使萤火虫算法适用于柔性车间调度问题, 设计一种贪婪式编码策略. 设有n个工件, 所有工件的工序总数为m,那编码由2m个整数组成的数组A, A[0]~A[m]表示工序加工顺序, A[m+1]~A[2m]表示机器选择顺序. 数组A的后半部分是利用贪婪思想进行机器选择, 以保证解码产生的调动为主动调度, 每道工序调用可加工的机器. 表1为柔性车间调度问题示例.
| 表 1 处理时间 |
编码过程如下所示:
前半部分表示工序, 根据表1示例, 随机生成长度为6, 由整数1, 2, 3组成的数组, 得到个体的前半部, 如图1所示.

|
图 1 工序加工顺序 |
根据所得个体前半部分的整数顺序, 解码得到工件加工顺序为O31-O11-O12-O21-O32-O22-O23-O33.
后半部分表示机器选择顺序, 本文利用贪婪思想进行机器选择, 以保证解码产生的调动为主动调度, 每道工序调用可加工的机器. 因此根据前半部分已得的工件加工顺序选择机器. 根据表1, 工序O31可由两台机器进行加工, 则编码为随机取1或2的整数. 如此得到得体的后半部分, 如图2所示.

|
图 2 机器选择顺序 |
根据所得个体后半部分的整数顺序解码得到各工序加工机器, O31由第一台机器进行加工, O11由第三台机器进行加工等.
将工序加工顺序编码与机器选择部分编码合并, 得到整个个体, 个体的前半部分表示工序编码, 个体的后半部分表示机器编码, 整个个体合并如图3所示.

|
图 3 整个个体 |
2.3 自适应选择策略
生物的免疫系统是机体执行免疫应答和免疫功能的重要系统, 它能够识别和清除外来的抗原体和内在的肿瘤细胞和癌细胞等作用. 因免疫算法较为复杂, 为避免复杂性, 本文选取几个重要的免疫操作, 摒弃复杂的交叉变异. 本文通过加入免疫算法中的抗体、亲和度, 来自适应调整步长参数.
在初始GSO算法中, 步长固定, 容易导致算法陷入局部最优解. 因此步长因根据每次迭代的结果, 不断调整其大小, 以便快速和准确的找到全局最优值, 比如在算法的迭代前期, 步长的变化需要大一些, 这样可以加快迭代速度, 在迭代后期, 步长需要很小, 目的是为了能准确的找到局部最优值. 因此将GSO算法和生物免疫搜索系统进行一个协同进化, 最终为每个个体找到最优步长.
首先为每个个体在一个合适的范围内随机分配抗体和步长, 根据算法的迭代情况计算每个抗体的亲和度, 并根据下式计算亲和度:
| ${\rm{A}}\left( {{{\gamma }}_{{i}}^{{G}}} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{c}}{\left| {\displaystyle\frac{{{{f}}\left( {{{x}}_{{i}}^{{G}}} \right){{ - f}}\left( {{{x}}_{{i}}^{{{G + 1}}}} \right)}}{{{{f}}\left( {{{x}}_{{i}}^{{{G + 1}}}} \right)}}} \right|,\;\;{\rm{if}}\;\;{{f}}\left( {{{x}}_{{i}}^{{{G + 1}}}} \right){{ < f}}\left( {{{x}}_{{i}}^{{G}}} \right)}\\{{\rm{0}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{others }}}\end{array}} \right.$ | (10) |
在每次迭代过程中, 一定百分比的抗体被一些新的抗体代替, 根据下式更新抗体.
| ${{\alpha }}_{{k}}^{{{G + 1}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}}{{{\alpha }}_{{{k + Q}}}^{{G}},\;\;\;{\rm{if}}\;\; Q + k \le {{M}}}\\{{{\upsilon }}_{{{Q + k - M}}}^{{G}},\;\;\;\;{\rm{otherwise}}}\end{array}} \right.$ | (11) |
其中, M=2*NP, Q=|0.2*NP|, k=1, 2,…, 2*NP.
根据一个随机的概率在抗体中选取步长参数, 并根据下式更新步长参数.
| $\gamma _i^{G{\rm{ + }}1}{\rm{ = }}\left\{\!\! {\begin{array}{*{20}{l}}{\pi _i^{G + 1},\;\;\;{\rm{if}}\;\;{{{P}}_i} \le {P_c}}\\{{\theta _i},\;\;\;\;{\rm{otherwise}}}\end{array}} \right.$ | (12) |
其中,i=1, 2,…, NP; Pi为rand,Pc为预设的接种概率,
位置更新过程中, 对三部分个体进行更新, 第一部分是个体自身i, 根据标准萤火虫算法进行更新. 第二部分在个体i的邻域范围内, 并且满足适应度值优于个体i的适应度值的个体, 采取POX交叉. 第三部分, 其余个体采用邻域交换或反序排序方法, 对个体进行位置更新.
(1) 第一部分
为使萤火虫算法适用于柔性车间调度问题, 针对问题特点, 对萤火虫的位置更新策略进行重新设置. 在标准萤火虫的位置更新的基础上重新排序, 首先针对个体的前半部分的工序进行重新排序, 后半部分在前半部分的基础上重新分配机器. 根据标准GSO算法位置更新公式得到非整数序列, 因此需对此序列进行优化, 使之符合柔性车间调度的实际状况. 首先选择比自己亮的个体, 因为步长参数的固定会使算法陷入局部最优, 因此上一小节利用自适应选择策略对步长参数进行自适应. 标准萤火虫算法位置更新结果如图4所示.

|
图 4 标准GSO位置更新结果 |
针对个体i的新位置的前半部分设置新的变化策略, 对于位置未发生变化的部分不进行变动, 对于位置发生改变的部分按大小进行排序即 0.87<2.06<3.06, 对新个体i的第1, 3, 6位置根据刚刚排序的大小所对应的位置, 将位置上的数字进行一一交换, 交换方式如图5所示.

|
图 5 标准GSO位置更新后的改动过程 |
将个体的前半部分更新整理后, 对个体的后半部分利用贪婪编码策略进行重新编码, 最终得到个体如图6所示.

|
图 6 标准GSO位置更新后的改动的结果 |
(2) 第二部分
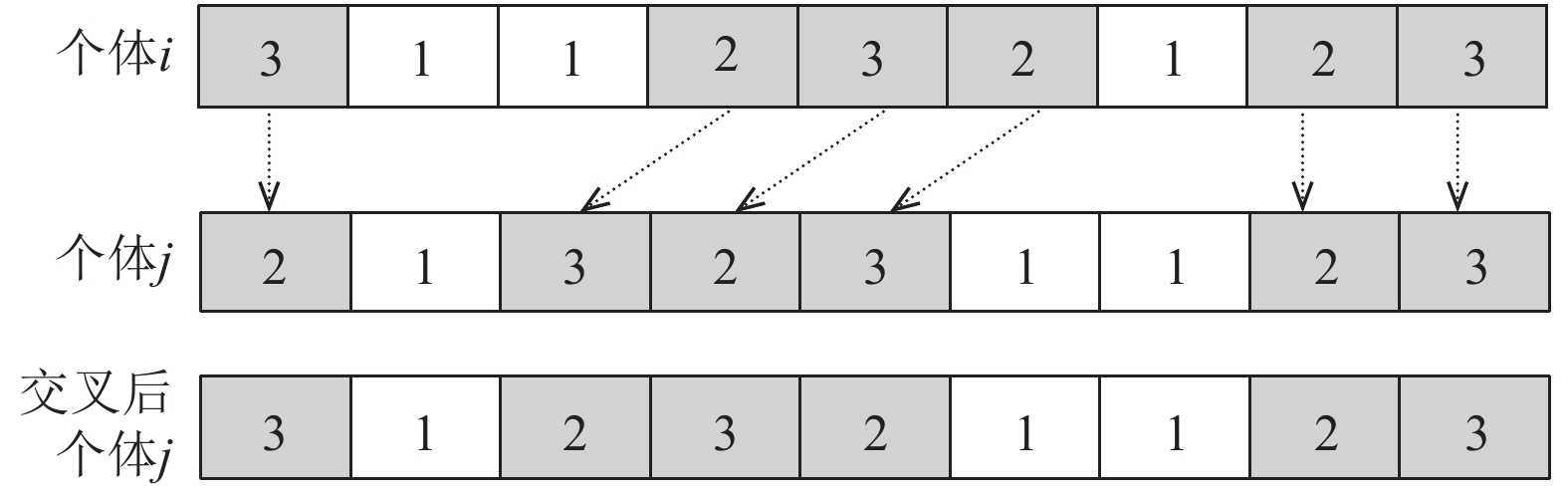
随机选择两个工件, 比如工件2和3, 对它们的工序进行整体POX交叉操作, 交叉过程如图7所示.
|
图 7 个体前半部分POX交叉操作 |
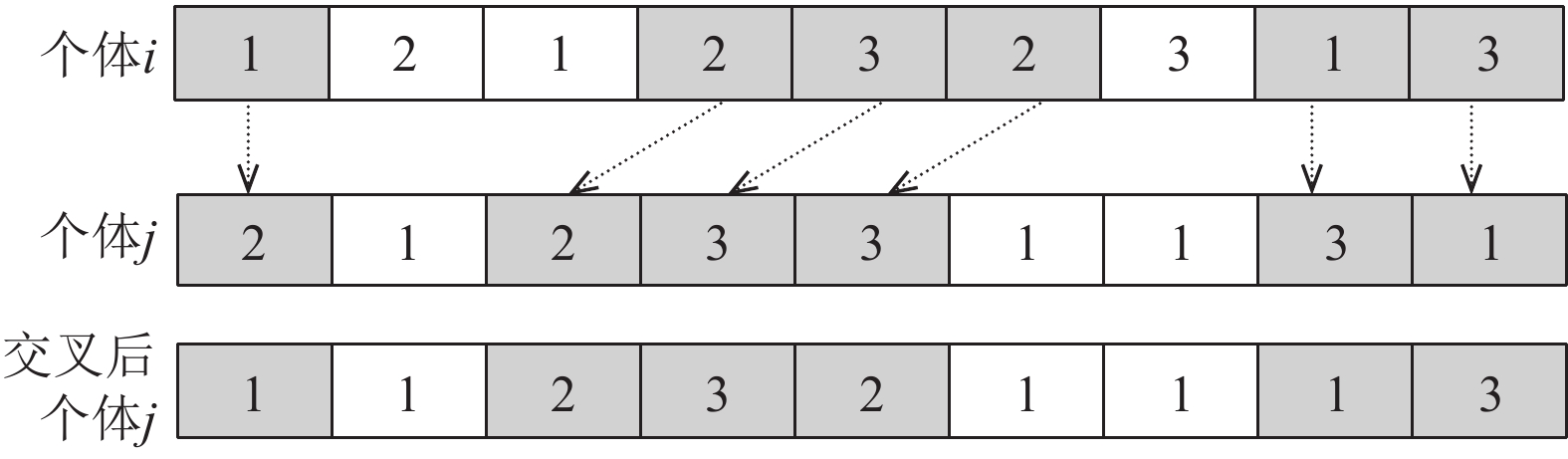
POX交叉后并没有工件整体的工序加工顺序发生变化, 因此只需根据工序变化的位置进行POX交叉, 交叉后得到机器选择顺序仍符合贪婪编码策略. 机器编码交叉过程如图8所示.
|
图 8 个体后半部分POX交叉操作 |
为加快算法收敛速度, 提高算法性能, 引入贪婪思想, 若POX交换后的个体小于原的适应度值, 则选择交换后的个体, 否则选择原个体.
(3) 第三部分
为提高种群的多样性, 提高算法全局搜索能力, 进行邻域插入, 或反序排序. 其具体操作如下所示.
1) 邻域插入. 随机选择两个位置1, 2, 将位置2基因插入位置1 基因的后面, 位置1与位置2间基因均向后移动. 其具体操作如图9所示.

|
图 9 个体前半部分邻域插入 |
2) 反序排序. 随机选择两个位置1, 2, 将位置1和位置2之间的基因进行反序排序. 其具体操作如图10所示.

|
图 10 个体前半部分反序排序 |
将个体的前半部分更新整理后, 对个体的后半部分利用贪婪编码策略进行重新编码. 为加快算法收敛速度, 提高算法性能, 引入贪婪思想, 交换后的个体小于原个体的适应度值, 则选择交换后的个体, 否则选择原个体.
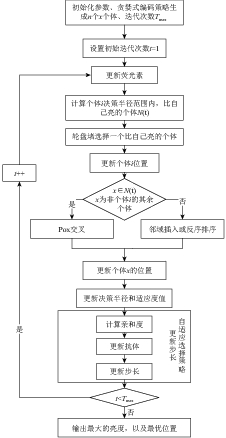
2.5 改进的GSO算法的流程图
|
图 11 改进的 GSO 算法的流程图 |
3 实验仿真 3.1 基准算例仿真
实验环境为Core i5 M480@2.67 Hz的CPU, 内存为4 GB RAM; 环境为Win10操作系统和Matlab2016a.
为验证本文算法有效性, 采用Kacem测试算例Brandimarte问题测试算例, 其中Kacem测试算例包括8×8, 10×10, 15×10三个柔性车间调度问题, 将本文算法与Chiang[11]提出的定位与控制遗传算法(AL-CGA), Xia等[12]提出的混合模拟退火与粒子群算法(PSO+SA), 吴秀丽等[13]提出的改进细菌觅食算法(IBFOA), 与马佳等[14]改进的人工免疫算法(AIA),进行对比. 各算法最优统计结果如表2所示.
| 表 2 Kacem实例最优解统计结果 |
从表2可知, 本文算法的求解结果小于或等于最新的其他四个算法的求解结果, 证明了本文算法在同类算法中的优越性能. 图12为问题求解10×10的最优甘特图.

|
图 12 10×10求解结果 |
对于10个测试Brandimarte算例将本文的离散萤火虫算法与吴秀丽等[13]提出的改进细菌觅食算法(IBFOA)、田旻[15]提出的分层混合遗传算法(HHGA)、Xing等[16]提出的改进的蚁群算法(KB-ACO)进行对比分析. 各算法最优统计结果如表3所示.
| 表 3 Brandimarte问题统计结果 |
从表3可以看出,在求解上述10个问题中, 本文算法得到的结果80%优于或等于KB-ACO得到的结果, 70%优于或等于IBFOA得到的结果, 80%优于或等于HHGA的结果. 实验结果表明, 和上述已有算法相比, 本文算法在求解FJSP问题具有一定的优越性.
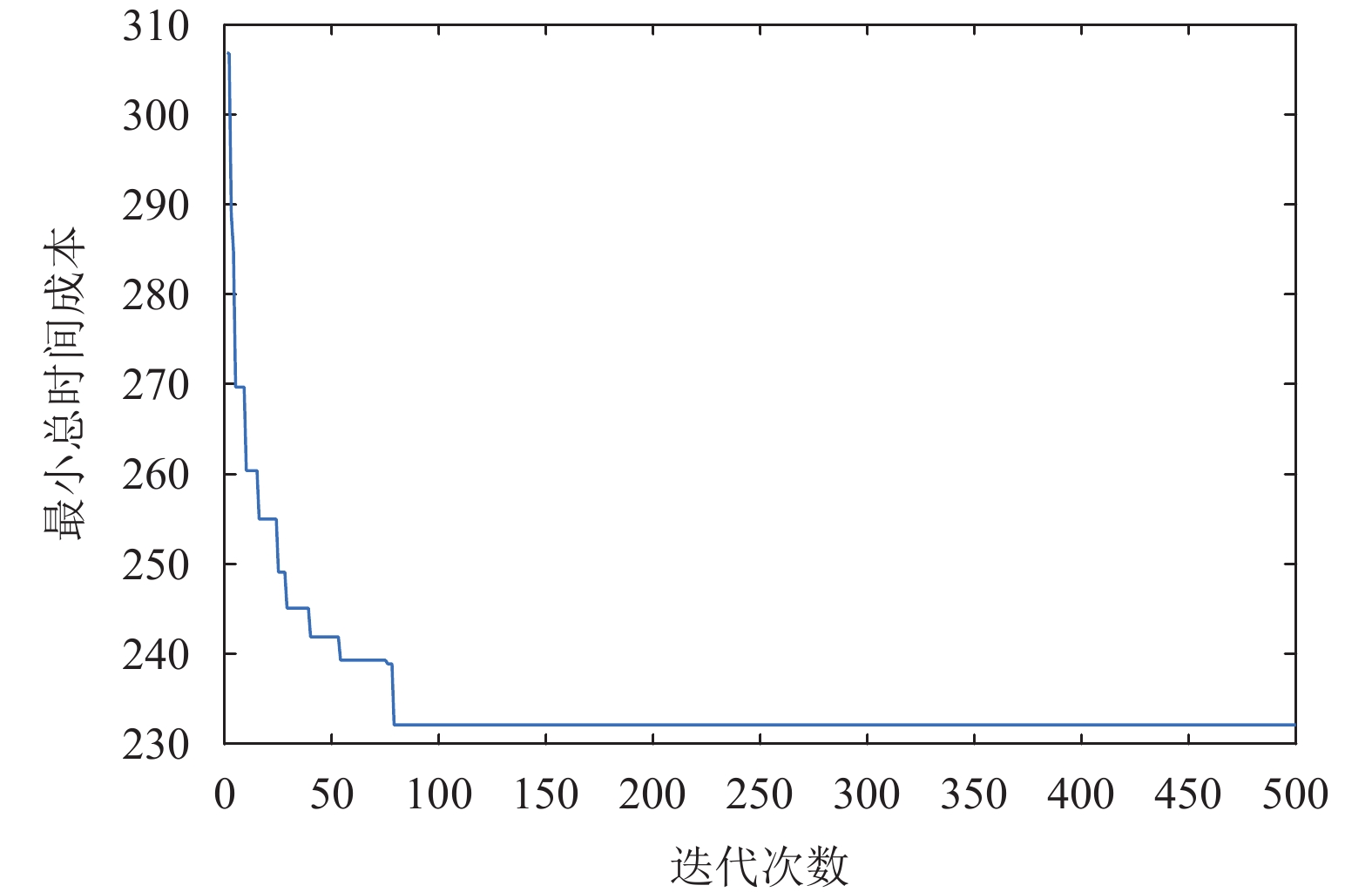
3.2 实例仿真以某公司的柔性制造单元调度为例进行仿真, 制造单元有3台加工设备,加工8种零件, 每种零件包括3道工序, 零件类型、交货期、加工时间表如表4所示, 根据企业预算和合同条款惩罚, 取提前惩罚系数为0.3, 拖期惩罚系数为0.7. 经过计算得到每个工件的完工时间、以及每个工件的惩罚成本, 如表5所示, 函数值变化曲线如图13所示, 最佳调度甘特图如图14所示.
| 表 4 工件加工信息 |
| 表 5 工件完工时间、惩罚成本 |
|
图 13 函数值变化曲线 |

|
图 14 最优调度甘特图 |
为进一步验证本文提出的调度算法在求解柔性车间E/T调度上的优越性, 与传统的离散算法GA, 与改进的NSGA-II算法进行对比分析, 算法的种群数目最最大迭代次数与本文算法相同, 得到的函数变化曲线与本文算法求得的变化曲线进行对比, 如图15所示.
由图15可看出, 本文算法迭代75次可找到最优值, 算法NSGA-II迭代110次找到最优值, 算法GA迭代490次达到最优值, 因此本文算法较其他两种算法收敛速度更快, 且本文算求解结果更优. 因此本文提出的改进的GSO算法在求解柔性车间E/T调度方面具有一定的有效性.
4 结束语针对机器资源和加工路线可选择情况下的柔性车间调度, 以最小最大完工时间和时间惩罚成本为目标建立柔性车间模型. 根据问题特点, 提出一种改进的GSO算法, 算法设计了一种具有贪婪思想的编码策略, 一个萤火虫个体表示工序加工顺序和工序加工位置; 采用自适应选择策略, 使步长自适应, 提高算法精度; 引入POX交叉、邻域交换和反序排序方法提高算法局部和全局寻优能力, 并利用贪婪思想, 提高算法的收敛速度. 通过实例仿真和算法比较验证算法性能, 实验结果表明改进的GSO求解柔性车间调度问题的有效性. 本文不足之处, 模型考虑因素较少, 之后将进一步优化算法性能, 尝试将本文算法用于机器故障情况下柔性车间调度问题.

|
图 15 函数曲线对比图 |
| [1] |
Pinedo M. Scheduling: Theory, algorithms, and systems. IIE Transactions, 1996, 28(8): 695-697. DOI:10.1080/15458830.1996.11770714 |
| [2] |
刘爱军, 杨育, 邢青松, 等. 多目标模糊柔性车间调度中的多种群遗传算法. 计算机集成制造系统, 2011, 17(9): 1954-1961. |
| [3] |
蔡霞, 李枚毅, 王康, 等. 基于浮点型编码策略的差分多目标柔性车间调度优化. 计算机应用研究, 2013, 30(4): 999-1003. DOI:10.3969/j.issn.1001-3695.2013.04.010 |
| [4] |
侯晓莉, 刘永, 江来臻, 等. 多目标FJSP的一维编码粒子群优化求解方法. 计算机工程与应用, 2015, 51(13): 47-51, 71. DOI:10.3778/j.issn.1002-8331.1408-0067 |
| [5] |
马立波, 王艳. 基于离散震荡粒子群算法的柔性作业车间调度优化方法. 机械制造与自动化, 2016, 45(2): 231-235. DOI:10.3969/j.issn.1671-5276.2016.02.065 |
| [6] |
薛宏全, 魏生民, 张鹏, 等. 基于多种群蚁群算法的柔性作业车间调度研究. 计算机工程与应用, 2013, 49(24): 243-248, 261. DOI:10.3778/j.issn.1002-8331.1306-0315 |
| [7] |
栾飞, 王雯, 傅卫平, 等. 基于PST层次结构的改进GA求解柔性车间调度问题. 计算机集成制造系统, 2014, 20(10): 2494-2501. |
| [8] |
徐华, 张庭. 新型离散蝙蝠算法求解柔性流水车间调度问题. 计算机工程与应用, 2016, 52(2): 262-265. DOI:10.3778/j.issn.1002-8331.1412-0353 |
| [9] |
傅卫平, 刘冬梅, 来春为, 等. 基于多色集合的改进遗传算法求解多品种柔性调度问题. 计算机集成制造系统, 2011, 17(5): 1004-1010. |
| [10] |
Krishnanand KN, Ghose D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics. Proceedings of the IEEE Swarm Intelligence Symposium. Pasadena, CA, USA. 2005. 84–91.
|
| [11] |
Chiang TC, Lin HJ. A simple and effective evolutionary algorithm for multiobjective flexible job shop scheduling. International Journal of Production Economics, 2013, 141(1): 87-98. DOI:10.1016/j.ijpe.2012.03.034 |
| [12] |
Xia WJ, Wu ZM. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems. Computers & Industrial Engineering, 2005, 48(2): 409-425. |
| [13] |
吴秀丽, 张志强, 杜彦华, 等. 改进细菌觅食算法求解柔性作业车间调度问题. 计算机集成制造系统, 2015, 21(5): 1262-1270. |
| [14] |
马佳, 石刚. 基于改进人工免疫算法的柔性车间调度问题. 计算机仿真, 2014, 31(12): 375-379. DOI:10.3969/j.issn.1006-9348.2014.12.083 |
| [15] |
田旻, 刘人境. 分层混合遗传算法求解柔性作业车间调度问题. 工业工程与管理, 2017, 22(5): 32-39. |
| [16] |
Xing LN, Chen YW, Wang P, et al. A knowledge-based ant colony optimization for flexible job shop scheduling problems. Applied Soft Computing, 2010, 10(3): 888-896. DOI:10.1016/j.asoc.2009.10.006 |
 2019, Vol. 28
2019, Vol. 28


