2. 北京师范大学研究生院 珠海分院, 珠海 519085
2. Zhuhai Branch, Graduate School of Beijing Normal University, Zhuhai 519085, China
随着以深度学习为代表的新一代人工智能算法的研究与快速发展, 建立在该方法之上的各种智能应用系统越来越依赖大数据的自主训练与学习, 特别是在一些复杂的智能应用系统, 如图像识别、语音识别、视频检索、自然语音处理等领域更是如此[1]. 深度学习对数据的依赖导致数据的体量和维度均出现指数级增长. 很明显, 过高的数据维度会造成维度灾难, 既影响了计算效率, 也影响分类性能[2]. 这就有必要采用某种方法来降低数据维度, 以此降低进一步数据处理的复杂度, 提高处理效率[3].
由于深度学习的本质依然是机器学习, 因此在降维处理方面可以借鉴传统的机器学习方法, 并在此基础上进行优化以适应深度学习的应用场景. 机器学习中较常采用的降维方法有: 主成分分析法(Principal Component Analysis, PCA)、线性判别分析法(Linear Discriminant Analysis, LDA)、局部线性嵌入法(Locally linear embedding, LLE)、拉普拉斯特征映射法(Laplacian Eigenmaps)等[4–7].
下面, 本文将以卷积神经网络获取图像特征为研究目标, 以Caltech 101 图像数据集为实验对象, 采用VGG-16深度卷积神经网络进行图像的特征提取. 在此基础上, 通过研究图像高维特征信息, 选取统计学中的PCA法作为降维处理方法, 并配合SVD分解算法降低处理的复杂度, 进而再通过以相似性对降维后特征进行精度比对, 来分析降维后不同维度图像特征的精度损失.
2 PCA降维 2.1 PCA原理主成分分析PCA也称主分量分析, 它是一种将原有的多个变量通过线性变换转化为少数几个新的综合变量的统计分析方法. 这些新变量(也称主成分)互不相关, 能有效地表示原变量的信息, 不丢失或尽量少丢失原有变量的信息). PCA追求的是在降维之后依然能够最大化保持数据的内在信息, 并通过衡量在投影方向上的数据方差的大小来判断该方向的重要性. 其基本数学原理如下:
设n维向量w是低维映射空间的一个映射向量, 则经过最大化数据映射后其方差公式如下:
| $\mathop {\max }\limits_w \frac{1}{{m - 1}}{\sum\limits_{i = 1}^m {({w^{\rm T}}({x_i} - \overline x )} ^2}$ | (1) |
式(1)中, m是参与降维的数据个数,
定义W为包含所有特征映射向量的列向量组成的矩阵, 该矩阵可以较好地保留数据中的信息, 该矩阵经过代数的线性变换可以得到一个优化的目标函数如下:
| $\mathop {\min }\limits_w tr({W^{\rm T}}AW),\;{\rm {s.t.}}{W^{\rm T}}W = I$ | (2) |
式(2)中tr是矩阵的迹, A是协方差矩阵, 表达式如下:
| $A = \frac{1}{{m - 1}}\sum\limits_{i = 1}^m {({x_i} - \overline x } ){({x_i} - \overline x )^{\rm T}}$ | (3) |
PCA的输出就是
PCA需要计算其特征值和正交归一化的特征向量, 这两个向量在实际应用中都会非常大, 直接计算非常困难, 通常会用SVD分解来解决这个问题[8].
SVD即Singular Value Decomposition, 它是处理维数很高的矩阵经常用的方法, 通过SVD分解可以有效的将很高维的矩阵分解到低维空间里面来进行求解. 通过SVD分解可以很容易的求解出高维矩阵的特征值和其相应的特征向量. SVD分解的基本原理如下:
设A是一个秩为r的
| $U = ({u_1},{u_2}, \cdots ,{u_r}) \in {R^{n \times r}}$ | (4) |
| $V = ({v_1},{v_2}, \cdots ,{v_r}) \in {R^{n \times r}}$ | (5) |
| $A = dig({\lambda _1},{\lambda _2}, \cdots ,{\lambda _r}) \in {R^{n \times r}},\;{\lambda _1} \ge {\lambda _2} \ge \cdots {\lambda _r}$ | (6) |
式(4)、(5)、(6)三式满足:
| $A = U{A^{\frac{1}{2}}}{V^{\rm T}}$ | (7) |
其中,
上述分解过程即为矩阵A的SVD分解, A的奇异值为
由于
| $\sum = \frac{1}{M}\sum\limits_{i = 1}^M {({x_i} - u)} {({x_i} - u)^{\rm T}} = \frac{1}{M}X{X^{\rm T}}$ | (8) |
因此求出构造矩阵为:
| $R = {X^{\rm T}}X \in {R^{M \times M}}$ | (9) |
由此求出
| ${u_i} = \frac{1}{{\sqrt {{\lambda _i}} }}X{v_i},i = 1,2, \cdots ,M$ | (10) |
该特征向量通过计算较低维矩阵R的特征值和特征向量而间接求出的, 从而实现从高维到低维的快速计算.
2.3 PCA特征降维流程在SVD分解中U一共有M个特征向量. 虽然在很多情况下M要比
1) 首先计算特征平均值构建特征数据的协方差矩阵;
2) 再通过SVD分解求解该协方差矩阵的特征值以及特征向量;
3) 求出来的特征值依次从大到小的排列以便于选出主成分的特征值;
4) 当选出了主成分的特征值后, 这些特征值所对应的特征向量就构成了降维后的子空间.
3 基于CNN的图像特征提取 3.1 CNN卷积神经网络卷积神经网络(Convolutional Neural Network, CNN)是深度学习技术中极具代表的网络结构之一, 在图像处理领域取得了很大的成功, 许多成功的深度学习模型都是基于CNN的[9,10]. CNN相较于传统的图像处理算法的优点之一在于可以直接输入原始图像提取人工特征, 避免了对图像复杂的前期预处理过程[11].
本文选取VGG-16作为CNN特征提取网络, VGG-16获得2014年ImageNet比赛的冠军, 在学界有很广泛的应用, 而且被验证为最有效的卷积神经网络之一[12]. VGG-16网络的总体结构共有16层, 其中包括13个卷积层和3个全连接层[13], 如图1所示.

|
图 1 VGG-16结构图 |
实验输入的图像像素大小为224×224, 输出层为1000维. 卷积神经网络的特点是靠近输入层的节点表示图像在低维度上的抽象, 而靠近输出层的节点表示图像更高维度的抽象. 低维抽象描述图像的纹理和风格, 而高维度抽象描述了图像的布局和整体特征, 因此高维度特征能够较好的表示图像的内容. 在本次实验中, 以卷积神经网络的fc3层的输出的高维度特征作为图像的特征向量, 由于fc3是网络的第三个全连接层, 根据网络结构, 它具有4096维的输出, 因此我们获得的特征维度就是4096.
3.2 数据集选取Caltech 101数据集是加利福尼亚理工学院整理的图片数据集, Caltch101包括了101类前景图片和1个背景类, 总共9146张图片, 其中有动物、植物、卡通人物、交通工具、物品等各种类别. 每个类别包括40-800张左右的图片, 大部分类别包括50张左右的图片. 图片的大小不一, 但是像素尺寸在300×200左右[14].
为了减少实验时的计算量, 本文从102类数据中选择了25类数据, 每类选择40张图片, 总共1000张图片. 这25类数据都属于动物(此举增加判别难度, 动物和动物比动物和其他类别更相近), 每类都选40张.
4 实验测试 4.1 实验环境搭建为使PCA降维后对普遍特征的影响效果进行一个比对, 本文以图像特征的相似度比对为精确度检验指标, 采用欧式距离作为相似度特征度量指标, 检验降维后图像特征与没有降维前的精度损失变化情况. 实验软件环境为Linux操作系统和Keras神经网络框架, 编程语言采用Python 3.5, 硬件为配置有支持支持CUDA的NVIDIA GPU显卡GeForce GTX 285、至强四核处理器和32 GB内存的PC机. 实验流程如图2所示.
4.2 实验结果采用VGG-16的fc3提取的特征有4096维, 当在1000张图片的数据集中进行特征比对, 能够在较快的时间内完成. 但是, 在真实的检索环境下, 图片库中的图片要远远大于1000, 此时数据的维度会显著的影响检索效率. 降低数据的维度是检索中非常重要的一个环节.
先分析降维的可行性, VGG-16原本用于ImageNet图像分类竞赛, 竞赛任务是对100多万张属于1000个类别的图片进行识别. 这1000类数据囊括了已知的各种类别的事物, 所以可以将VGG-16定义为一个泛化的神经网络, 即对于各种类别的事物都具有学习能力. 然而实验的数据集仅仅具有25类, 且均为动物, 可以视为ImageNet数据集的一个子集. 但是使用一个大数据集的特征来描述其子集的特征是会存在冗余的.

|
图 2 实验流程图 |
本实验采用PCA去除数据集中的冗余, PCA通过线性映射将高维空间的数据投影到低维空间中, 并且尽量使低维空间上数据的方差尽量大. 这样在保持原有数据点关系不变的情况下能够有效的降低维度. 基于此原理, 实验使用PCA降维, 统计降维后维度与精确度的数据如表1所示.
| 表 1 PCA不同维度的相似度精度比对值 |
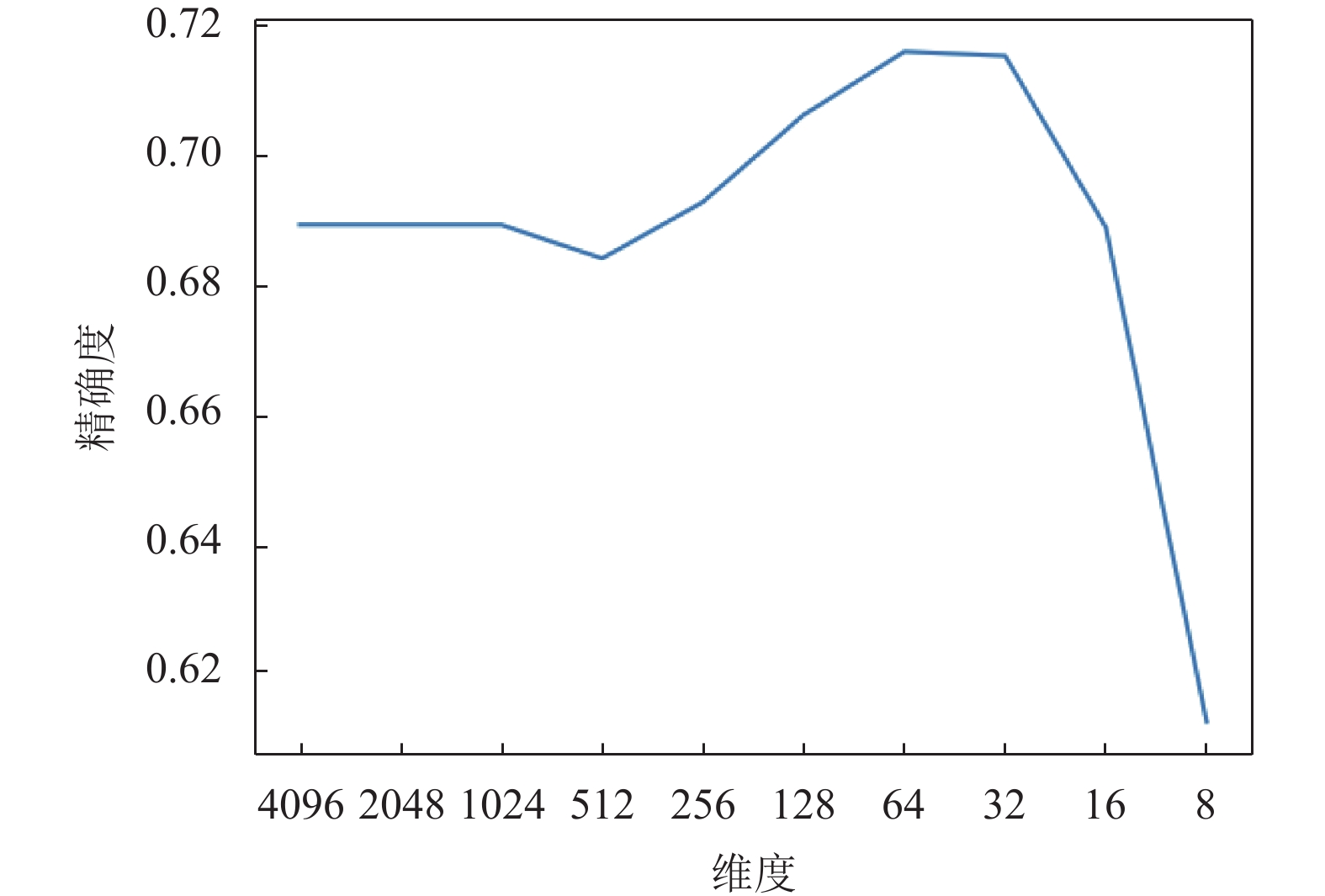
对应的变化折线图如图3所示.
5 结论从实验的数据变化和曲线表现来进行分析, 本实验获得两点结论.
1) 进行PCA降维后, 并没有产生精度的损失, 相反, 当维度降低到64的时候, 精度最高, 相比于不降维的情况, 提高了2.7%. 分析折线图可以看出, 维度从4096降到8维经历了缓慢上升和快速下降两个阶段. 第一个阶段从4096维到64维, 这个阶段的缓慢上升, 原因是由于冗余信息的去除导致的. 实验结果证明, CNN特征也有一定的信息冗余, 信息冗余所带来的影响比降维所带来的损失的影响要更大, 因此去除冗余能够提升准确率. 第二个阶段从64维到8维, 这个阶段准确率急速下降, 这是因为特征维度小于64后, 降低维度会去除有用信息, 有用信息受损, 导致了准确率的急速下降.
|
图 3 PCA降维后的比对准确率折线图 |
2) 进行PCA降维后, 除欧式距离外, 其他相似性度量的准确率都非常低. 产生这个现象是因为PCA计算时仅仅保证低维空间上数据的方差尽量大. 在仅考虑方差的降维条件下, 其他相似性度量方式失效就不难理解了.
综合以上实验得出: 当提取VGG-16神经网络fc3层的4096维特征, 使用PCA降至64维, 并采用欧氏距离作为相似性度量时依然能够获得最高的准确率, 保持最佳的图像特征信息.
| [1] |
Jose C. A fast on-line algorithm for PCA and its convergence characteristics. IEEE Transactions on Neural Network, 2000, 4(2): 299-305. |
| [2] |
Majumdar A. Image compression by sparse PCA coding in curvelet domain. Signal, Image and Video Processing, 2009, 3(1): 27-34. DOI:10.1007/s11760-008-0056-5 |
| [3] |
Gottumukkal R, Asari VK. An improved face recognition technique based on modular PCA approach. Pattern Recognition Letters, 2004, 25(4): 429-436. DOI:10.1016/j.patrec.2003.11.005 |
| [4] |
Mohammed AA, Minhas R, Wu QMJ, et al. Human face recognition based on multidimensional PCA and extreme learning machine. Pattern Recognition, 2011, 44(10-11): 2588-2597. DOI:10.1016/j.patcog.2011.03.013 |
| [5] |
Kuo CCJ. Understanding convolutional neural networks with a mathematical model. Journal of Visual Communication and Image Representation, 2016, 41: 406-413. DOI:10.1016/j.jvcir.2016.11.003 |
| [6] |
Schmidhuber J. Deep learning in neural networks: An overview. Neural Networks, 2015, 61: 85-117. DOI:10.1016/j.neunet.2014.09.003 |
| [7] |
Girshick R. Fast R-CNN. 2015 IEEE International Conference on Computer Vision. Santiago, Chile. 2015. 1440–1448.
|
| [8] |
Szegedy C, Liu W, Jia YQ, et al. Going deeper with convolutions. 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA. 2015. 1–9.
|
| [9] |
Rampasek L, Goldenberg A. TensorFlow: Biology’s gateway to deep learning?. Cell Systems, 2016, 2(1): 12-14. DOI:10.1016/j.cels.2016.01.009 |
| [10] |
Sebe N, Tian Q, Lew MS, et al. Similarity matching in computer vision and multimedia. Computer Vision and Image Understanding, 2008, 110(3): 309-311. DOI:10.1016/j.cviu.2008.04.001 |
| [11] |
Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [12] |
Zhuang FZ, Luo P, He Q, et al. Survey on transfer learning research. Journal of Software, 2015, 26(1): 26-39. |
| [13] |
Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada. 2015. 1135–1143.
|
| [14] |
Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. 13th European Conference on Computer Vision. Zurich, Switzerland. 2014. 818–833.
|
 2019, Vol. 28
2019, Vol. 28


