图像的纹理分类作为图像处理应用中的一个重要方面, 其现实意义在于可以对某些未知类别的图像样本集根据其纹理的差异进行归类, 而且纹理分析技术一直是计算机视觉、图像处理、图像分析、图像检索等的活跃研究领域, 在遥感图像处理、工业产品识别等众多科学领域都起着关键作用. 对于图像的纹理特征可以分为结构方法、统计方法、模型方法和变换方法^[1]. 铝铸件作为一种建筑门窗、幕墙、室内外装饰及建筑结构常用的工业型材, 其表面质量尤其受到重视, 在针对不同的型材进行表面缺陷检测时候需要对其类型进行自动识别来匹配检测参数. 由于不同的型材往往对应着不同的纹理, 所以可以根据其表面不同的纹理对其进行合理的分类. 但是由于传统的工业生产方式的限制, 还没有一种方法被应用于解决此问题, 因此研究设计一种自动化识别型材种类的方法显得十分必要.

在众多的纹理特征中, 1973年由Haralick提出的灰度共生矩阵法作为统计方法中的代表有着很强的适应性, Clausi对灰度共生矩阵进行了深入的分析并做了较好的改进^[2]. Arebey等采用灰度共生矩阵提取垃圾箱俯拍图像纹理特征进行分类^[3]. Amol等采用灰度共生矩阵进行虹膜识别^[4]. 而Gabor小波滤波, 是一种重要的基于变换的纹理特征提取方法, 该方法借鉴心理生理学的研究成果, 模拟了一些方向可选神经元的计算机制, 通过把Gabor函数作为小波变换的基函数, 来实现对图像的多方向和多尺度的特征提取, Shen等人使用Gabor小波变换进行了相应的改进^[5], 并结合了LBP特征, 使用最近邻分类法对硬币图像进行分类识别, 得到了很好的结果. Yang等人使用Gabor纹理特征进行人脸识别应用的研究, 并对比了多种分类器的分类识别结果^[6]. Rahman等人研究了Gabor小波纹理特征的旋转、尺度不变性特点, 在基于内容的图像检索中取得了很好的结果^[7]. 另外, 对于不同特征的融合研究. Cui等人采用图像融合和小波去噪进行了肋骨分割及特征提取^[8,9].

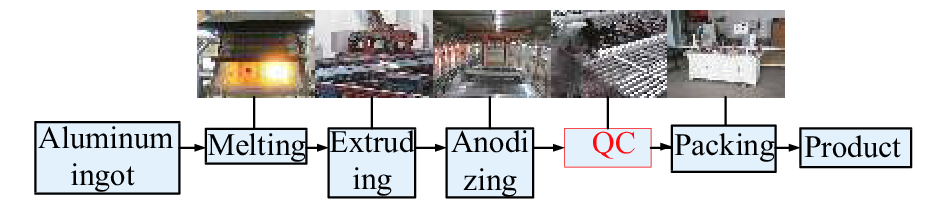
1 纹理特征提取及分类

铝铸件生产包括熔铸(Melting)、挤压(Extruding)、氧化(Anodizing)、检测(QC)、包装(Packing)等几个过程. 熔铸过程中可能会混入杂质, 使得铝铸件材质不符合要求; 挤压过程中容易造成气泡和划痕等缺陷; 氧化过程中容易有氧化不均匀等; 如图1所示, 而我们的工作就是在检测阶段用机器视觉技术代替人工检测, 避免了人工检测过程中不稳定因素对质量检测结果的干扰, 能够最大程度的检测出铝铸件不同种类的表面缺陷, 保证检测缺陷的速度、精度以及一致性.

不同的应用场合需要有不同的铝铸件. 中国铝铸件约有300种合金、1500个品种, 是世界上产品品种最丰富的国家之一. 它们有不同的形状、结构、颜色、质地等. 如图2所示展示了几种不同的铝铸件. 在质量检测中, 人类可以轻易忽略铝型材的结构和质地等本质特征, 只关注其表面缺陷. 然而, 计算机很难识别图案是否是缺陷或者轮廓纹理.

1.1 基于灰度共生矩阵的图像纹理特征提取

由于纹理是由灰度分布在空间位置上反复出现而形成的, 因而在图像空间中相隔某距离的两象素之间会存在一定的灰度关系, 即图像中灰度的空间相关特性. 灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法. 灰度共生矩阵定义为图像中相距为 $\delta = \left( {\Delta {x}, \Delta y} \right)$ 的两个灰度像素同时出现的联合概率分布. 设图像的灰度级为N, 则共生矩阵是N×N矩阵, 可表示为 ${P_\delta }(i, j)$ , 其中位于 $(i, j)$ 的元素 $p(i, j)$ 的值表示一个灰度为 $i$ 而另一个灰度为 $j$ 的两个相距为 $\delta = \left( {\Delta {x}, \Delta y} \right)$ 的像素对出现的概率. 在实际处理中, 为了减少计算量, 通常 $\left( {\Delta {x}, \Delta y} \right)$ 取以下四个方向, 如图3所示.

计算灰度共生矩阵(0°方向). 根据灰度压缩后的图像矩阵计算N×N阶灰度共生矩阵 ${P_\delta }(i, j)$ (例如这里N=4), $\delta $ 为距离. 元素值计算例如: 当 $\delta = \left( {\Delta {x = 1}, \Delta y=0} \right)$ , 则像素对(0, 2)出现的次数为2, 且矩阵为对称矩阵. 则共生矩阵中 $p(0, 2){ =}p(2, 0){=}2$ , 以此类推.

根据灰度共生矩阵可以最多得到14个纹理特征向量, 实际使用中根据需要选择特征值, 求解以下特征值, 构成特征向量.

对比度: $ CON = \sum\limits_{{i} = o}^{n} {\sum\limits_{{j} = o}^{n} {{{\left( {i - j} \right)}^2}} } p({i, j})$

能量: $ ASM = \sum\limits_{{i} = o}^{n} {\sum\limits_{{j} = o}^{n} {{p^2}({i, j})} }$

熵: $ ENT = - \sum\limits_{{i} = o}^{n} {\sum\limits_{{j} = o}^{n} {p({i, j})} } \log p(i, j)$

相关性: $ COR = \frac{1}{{{\sigma _x}{\sigma _y}}}[\sum\limits_{{i} = o}^{n} {\sum\limits_{{j} = o}^{n} {i \times j \times p({i, j})} } - {\mu _x}{\mu _y}]$

逆差矩: $ {\rm{IDM}} = \sum\limits_{{i} = o}^{n} {\sum\limits_{{j} = o}^{n} {p({i, j})} } /(1 + {(i - j)^2})$

1.2 基于Gabor小波的图像纹理特征提取

Gabor小波对于图像的边缘敏感, 能够提供良好的方向选择和尺度选择特性, 而且对于光照变化不敏感, 能够提供对光照变化良好的适应性. 使用Gabor方法的基础是认为纹理是窄带宽的信号, 主要思想是: 不同的纹理一般具有不同的带宽和中心频率, 根据不同的频率和带宽设计一组Gabor滤波器对纹理图像滤波, 不同的滤波器只能通过相应的纹理, 限制其他纹理. 通过对每个滤波器的输出结果分析, 提取纹理特征, 用于后续工作. Gabor滤波器提取纹理特征主要包括两个过程: 设计滤波器、从滤波器的输出结果中提取有效的纹理特征集, 二维离散Gabor小波变换过程描述如下式所示:

${I_{p, q}}({ x, y}) = \sum\limits_s {\sum\limits_t {f({ x - s, y - t})} } \varphi {*_{p, q}}({ s, t})$

首先选取Gabor滤波器组的方向数p、尺度数q, 以及方差等参数构造Gabor小波滤波器组. 如p=6, q=4所示, 则最终构造出的小波基函数就有4×6=24个, 即通过这24个滤波器会最终会得到24个变换图像(通过与源图像卷积计算); 然后得到不同方向和尺度的Gabor滤波器以后, 对图像滤波(卷积)得到相应的变换后图像, 分别提取各个变换后图像的特征, 如基于Gabor滤波器的输出的幅度响应、Gabor能量特征、复矩特征、栅格元特征、独立成分分析法等等.

1.3 SVM分类

支持向量机(Support Vector Machine, SVM)^[10], 在解决小样本、非线性即高维模式识别中表现出许多特有的优势, 并能够推广应用到函数拟合等其他机器学习问题中. 支持向量机方法是建立在统计学习理论的基础上的, 根据有限的样本信息在模型的复杂性和学习能力之间需求最佳折衷, 一起获得最好的推广能力(或称泛化能力). SVM擅长应付样本数据线性不可分的情况, 主要通过松弛变量和核函数技术来实现的, 这是SVM的精髓. 与传统的经验风险最小化原理相比, 在一定程度上克服了“维数灾难”和“过学习”等传统困难, 为研究有限样本情况下的统计模式识别和更广泛的机器学习问题建立了一个较好的理论框架. 支持向量机性能的优劣主要取决于核函数及其参数的选择, 其中核函数的选择更加重要.

2 特征提取及训练

分别采用灰度共生矩阵和Gabor小波滤波两种方法对图像进行特征提取, 并借助libSVM对其进行分类预测, 图2是用于需要分类识别的铝铸件的9种型材.

实验的中各个算法中都需要对图像进行分割, 去除背景以避免其对提取特征结果的影响, 这里我们是通过OpenCV库内封装的函数将BMP格式的图像读入, 并转换为灰度图, 存储在IplImage*指向的结构中, 每个像素值为char值. 然后将整个灰度图的数据存放到以图像的高和宽作为矩阵行列的double类型的矩阵中, 进行char到double的转换, 然后通过霍夫变换^[11]对图像进直线检测, 检测出型材的上下边界, 得到需要提取特征的范围, 为后续的共生矩阵求解和Gabor小波滤波变换做准备.

使用了四种方法对铝铸件图像进行特征提取: 灰度共生矩阵、Gabor小波变换纹理特征, 灰度共生矩阵和Gabor小波变换纹理特征, 以及根据铝铸件的特点将Gabor小波变换纹理特征和检测出的直线特征.

灰度共生矩阵特征提取算法: 灰度压缩为8级, 步长距离选择为1, 即对目标像素点求解其与相邻像素的关系, 以计算0°, 45°, 90°, 135°四个方向图像的灰度共生矩阵. 分别计算四个方向共生矩阵的能量、熵、对比度、逆差矩、相关性五个统计值的均值和方差共十个值作为图像最终的特征值, 如下式所示:

${F_{GLCM}} = [{\mu _{ASM}}, {\sigma _{ASM}}, {\mu _{ENT}}, {\sigma _{ENT}},\cdots, {\mu _{CON}}, {\sigma _{CON}}]$

Gabor小波变换纹理特征: 根据铝铸件纹理特点, 算法中我们使用以下方向和尺度组合, 如表1所示:

根据不同的方向和尺度, 得到不同的Gabor小波核用于对图像进行滤波变换, 然后对变换后的图像进行计算, 得到图像的均值和标准方差, 得到2×O×S维的特征向量, 如下式所示:

${F_{\rm{Gabor}}} = [{\mu _{0, 0}}, {\sigma _{0, 0}}, {\mu _{0, 1}}, {\sigma _{0, 1}},\cdots, {\mu _{O - 1, S - 1}}, {\sigma _{O - 1, S - 1}}]$

共生矩阵和Gabor纹理特征的融合, 即将提取到的共生矩阵和Gabor纹理特征组在一起构成新的特征向量用于型材分类, 如下式所示:

${F_{\rm{Gabor}}}_{ + {\rm{GLCM}}} = {F_{\rm{Gabor}}} \cup {F_{\rm{GLCM}}}$

根据铝铸件特点, 为了提高识别准确率, 根据之前检测出的直线, 对型材型进行区域分割, 并以直线代表图中纹理, 计算直线所占图像像素比例, 作为另一特征和Gabor纹理特征进行组合, 如下式所示:

${F_{\rm{Gabor}}}_{ + Line} = {F_{\rm{Gabor}}} \cup Line$

最后, 我们使用SVM算法对提取到的特征进行分类模型的训练, 得到训练模型用于对测试集的测试, 我们在这里核函数选择RBF核, 通过参数调优, 惩罚系数选择为100, $\sigma $ =0.5.

3 实验结果

实验在PC上进行系统仿真, 配置为 Intel 2.2 GHz CPU, 4 GB内存, 软件平台为Windows 7下未进行优化的VS 2010, 集成OpenCV 2.5对图像进行处理及特征提取, 并借助于libSVM工具包对特征进行模型训练, 用以对未知类型型材的识别. 采用的实验对象包括九种类别共180幅图像的训练集, 和同样包括九种类别共90幅图像的测试集(均为实物图像), 根据上述方法, 实验结果如表2所示.

从实验结果可以看出, 共生矩阵法无论是在图像特征提取还是类型识别上都是速度最快的, 但是准确率不是很高, 只有71%. Gabor小波变换提取图像纹理特征, 虽然速度上比较慢, 但是准确率却是很高的, 最高达到了98.9%, 另外, 将Gabor纹理特征和共生矩阵纹理特征合并在一起之后, 有效提高识别准确率, 特征提取时间也没有很大的改变, 这说明两种特征融合会相互不会影响. Gabor纹理特征和直线比率特征进行融合, 从特征提取时间以及识别时间上和单独用Gabor纹理特征区别不大, 准确率上也不相上下.

从各个时间上来看, 无论是灰度共生矩阵还是Gabor小波变换, 大部分都花费在特征提取的过程中, 所以后续的工作需要在保证识别准确率的情况下, 优化特征提取的过程.

灰度共生矩阵并不适合像铝铸件这种纹理比较简单且训练集不大的图像的识别, 尤其是纹理比较单一的图像. 通过Gabor小波变换提取图像纹理特征更具有通用性, 是比灰度共生矩阵更好的纹理特征表现形式, 但是方向尺度过多的话, 因为涉及到矩阵的卷积计算, 其计算量会比较大, 效率会大大降低, 所以想要符合实时应用, 在特征提取的时间上还有待优化.

4 结论及展望

本文从四个角度对铝铸件图像进行特征描述, 并借助与libSVM对特征进行分类识别, 通过实验可以看出, 本文使用的方法对于铝铸件的类型识别是可行的, 由于铝铸件纹理比较单一简单, 所以灰度共生矩阵虽然速度比较快, 但是准确率偏低; Gabor小波变换由于计算量比较大, 所以耗费的时间更长一些, 但是准确率很高; 将两种特征综合以后, 时间上没有区别, 准确率上还有微弱改善; 整合直线比率特征以后没有明显差别. 由于在提取特征时耗费时间太长, 本文在下一步工作中将对特征提取过程进行优化.