引言

能源消耗已经成为我们社会中的一个非常重要的问题, 制造业中的能耗需求就占了总能耗的33%, 释放的 ${\rm{C}}{{\rm{O}}_{\rm{2}}}$ 占到总量的38%^[1]. 同时随着能源需求和价格的增加, 实际生产过程产生大量与生产不直接相关的能源消耗, 结合制造业中瓶颈工序的问题, 引入批调度在提高生产管理水平和经济效益方面有着十分重要的现实意义, 而且对于批调度很早就开始研究, Ikura和Gimple^[2]首次对批调度问题进行了研究, 其中批的加工时间为常数; Uzsoy^[3]首次提出并研究了目标为极小化完工时间( ${C_{\max }}$ )的差异工件单机批调度问题, 并证明为NP难问题. 同时随着对节能问题关注程度的日益提升, 近来越来越多的学者对节能调度进行了研究, Pechmann和Scholer^[4]通过减少热量泄露来达到保温效果, Yu等^[5]应用多目标遗传算法对建筑设计中的节能和热舒适性进行优化, Gong等^[6]使用一个通用的方法来对节能问题进行研究, 以提高单元产品的生产性价比, 但是, 在批处理机调度中同时考虑时间和能耗的研究却很有限, Melouk等^[7]和Damodaran等^[8]分别使用基本的模拟退火法和遗传算法仅对完工时间进行求解, 而Shrouf等^[9]和Che^[10]分别使用遗传算法和混合的数学规划法仅考虑能耗成本, 没有考虑与生产性能相关的完成时间, Oron^[11]利用数学方法对能耗成本和总完成时间分开进行考虑. 考虑到环境的压力, 降低车间能耗对制造商是很有吸引力的, 不仅表现在环境方面, 在经济上也是如此, 这也是为什么越来越多的科学家致力于节能和减少制造业中碳排放的原因^[12], 因此在同时考虑经济和环境下采取有效的节能措施来减少能耗问题是很有必要的^[13].

本论文应用的背景主要是眼镜镜片的加热回火过程, 因为镜片毛坯通常由质地相对柔软的玻璃制成, 装入镜架前必须通过加热进行回火, 以增加强度, 而不同规格的镜片按照不同的固化曲线和控制程序进行加工, 固化时间也存在差异. 所以由于顾客产品尺寸不同, 种类的差异导致的加热时间不同, 可以看成差异工件的问题, 同时把加热的熔炉看作资源, 很多不同尺寸, 不同种类的镜片同时放入熔炉中进行加热, 可以把这些同时进行处理的镜片看成一批工件, 而所有工件尺寸和不能超过熔炉的容量, 加热过程中不允许中断. 在同时考虑生产效率和能源消耗下, 把最小化完成时间( ${C_{\max }}$ )和总能耗成本(TEC)作为调度的目标函数, 使用偏好矩阵 $({\omega _c},{\omega _e})$ 在 ${C_{\max }}$ 和TEC之间寻找平衡. 在优化过程中, 对分批引入左移调度进行批的局部改进, 使用改进的选择算子, 同时能耗计算时考虑分时计价原则.

本文组织如下, 第二部分为问题描述和数学建模; 第三部分主要介绍遗传算法在考虑能耗的单机批调度中的应用; 第四部分为相关实验; 第五部为结论与展望.

1 问题描述 1.1 相关定义

本论文是遗传算法在考虑能耗的单机批调度中的应用, 目标为最小化完工时间( ${C_{\max }}$ )和最小化能耗总成本(TEC).

为了方便目标解的计算, 需要对调度过程中的机器状态进行说明, 加工状态(processing), 待机状态(idle), 关机状态(shutdown). 各种状态的转换如图1. 其中 $\left( {\begin{array}{*{20}{c}} t \\ e \end{array}} \right)$ 表示 $ t $ 单位时间内消耗 $ e $ 单位能耗.

加工与关机之间的转化需要考虑, 等待和关机之间可以通过加工状态间接转化, 所以不需要考虑直接转化, 而加工与等待之间的转化时间太短而不需要考虑.

1.2 数学模型 1.2.1 假设和约束

(1) 工件集合 ${{J}} = \{ 1,2, \cdots, N\} $ , 工件j的加工时间 ${p_j}$ , 尺寸 ${s_j}$ , 加工功率 ${e_j}$ .

(2) J中工件分批加工, 任一批中的工件集合 ${{{B}}^b}$ , 其中工件总尺寸和不超过机器容量C.

(3) 加工不允许中断, 批b的加工时间 ${P^b}$ 为 ${B^b}$ 中所有工件最大加工时间, 批b的功率 ${E^b}$ 为 ${B^b}$ 中所有工件的最大加工功率.

(4) 目标是如何安排生产, 使得 ${C_{\max }}$ 最小和TEC最少.

1.2.2 数学表达式形式

(1) 集合

J: 工件集合 $J = \{ 1,2, \cdots, N\} $ .

B: 批次集合 $B = \{ {b_1},{b_2}, \cdots, {b_m}\} $ .

T: 单位时间集合 $T = \{ {t_1},{t_2}, \cdots, {t_n}\} $ .

S: 机器状态集合, S={1,2,3}, 1表示加工, 2表示待机, 3表示关机.

(2) 参数

${c_t}$ : t时刻单位电价.

${E_s}$ : 机器为状态s时的单位功率.

${E_{s{s'}}}$ : 机器状态转换的单位功率.

${T_{s{s'}}}$ : 机器状态转换的时间.

${p_j}$ : 工件加工时间.

${P^b}$ : 批的加工时间.

${E^b}$ : 批的加工功率.

$s{t^b}$ : 批的开始时间.

$c{t^b}$ : 批的完成时间.

$y_j^b$ : 工件j在b批中时 $y_j^b{\rm{ = }}1$ , 反之 $y_j^b{\rm{ = 0}}$ .

$s_b^t$ : 批b在t开始加工时 $s_b^t{\rm{ = }}1$ , 反之 $s_b^t{\rm{ = }}0$ .

$\chi _b^t$ : 批b在t处于加工状态时 $\chi _b^t$ =1, 反之 $\chi _b^t$ =0.

$\alpha _s^t$ : 机器t处于s状态时 $\alpha _s^t$ =1, 反之 $\alpha _s^t$ =0.

$\beta _{s{s'}}^t$ : 机器t处于转换过程时 $\beta _{s{s'}}^t$ =1, 反之 $\beta _{s{s'}}^t$ =0.

(3) 问题的数学模型

$Min{C_{\max }}$

(1)

$Min\sum\limits_{t \in T} {{c_t}[\sum\limits_{b \in B} {{E^b}} \chi _b^t + \sum\limits_{s = 2} {{E_s}} \alpha _s^t + \sum\limits_{s,{s'} \in S} {{E_{s{s'}}}} \beta _{s{s'}}^t]} $

(2)

${\rm{s.t.}}\;\;\;\sum\limits_{b \in B} {y_j^b = 1,\;\;j \in J} $

(3)

$\sum\limits_{j = 1}^N {{s_j}} y_j^b \leqslant C,\;\;b \in B$

(4)

${P^b} = \max\{ {p_j}y_j^b\} ,\;\;j \in J,b \in B$

(5)

${E^b} = \max\{ {e_{\rm{j}}}y_j^b\} ,\;\;j \in J,b \in B$

(6)

$\sum\limits_{j = 1}^N {\frac{{{s_j}}}{C}} \leqslant m \leqslant N$

(7)

$\sum\limits_{b \in B} {\chi _b^t} \leqslant 1,\;\;t \in T$

(8)

$t \geqslant s{t^b} - (1 - \chi _b^t){P^b},\;\;b \in B$

(9)

$t \leqslant c{t^b} - 1 + (1 - \chi _b^t){P^b},\;\;b \in B$

(10)

$\sum\limits_{b \in B} {\chi _b^t} = \alpha _1^t,\;\;t \in T$

(11)

$\sum\limits_{s \in S} {\alpha _s^t} + \sum\limits_{s,{s'} \in S} {\beta _{s{s'}}^t} = 1,\;\;t \in T$

(12)

$\alpha _s^t \leqslant \sum\limits_{{s'} \in S,{T_{s{s'}}} = 0} {\alpha _{{s'}}^{t + 1} + \sum\limits_{{s^{''}} \in S,{T_{s{s^{''}}}} \geqslant 1} {\beta _{s{s^{''}}}^{t + 1}} } ,\;t \in T,t \ne card(T)$

(13)

$\beta _{s{s'}}^t \leqslant \beta _{s{s'}}^{t + 1} + \alpha _{{s'}}^{t + 1},\;\;t \in T,s \in S,{s'} \in S,{T_{ss'}} \geqslant 1$

(14)

$\begin{aligned} s_{{b'}}^{{t'}} \leqslant \sum\limits_{{t'} \leqslant t} {s_b^t} ,\;&{b} = 1,2, \cdots, m,\;b' = 1,2, \cdots, m,\;{b'} \leqslant b,\\ & {t} \in T,t' \in T\end{aligned}$

(15)

式(1)和(2)为目标问题; 式(3)保证每个工件只属于一个批; 式(4)保证每个批中工件总尺寸不超过机器总容量; 式(5)(6)说明批的加工时间为批中工件最长加工时间; 批的加工功率为批中工件最大加工功率; 式(7)给出总批数的取值范围; 式(8)保证每个时刻只能处理一个批; 式(9)(10)保证处理不被打断; 式(11)保证加工批时机器处于加工状态; 式(12)保证机器的状态; 式(13)(14)保证只有前一个操作结束后才能进行下一个操作; 式(15)保证批的顺序.

2 遗传算法在考虑能耗的单机批调度中的应用 2.1 编码与初始种群的产生

本文采用基于工件序列的编码方式, 每个工件都用唯一的自然数表示, 对于N个工件的调度问题, 随机产生1到N的一个排列, 每个位置上的数字表示对应的工件号, 个体就用这组数字串表示. 而种群的大小根据研究问题的规模而定, 本论文中初始种群大小为20, 采用随机方法产生一组初始种群.

2.2 目标的评估

本论文的目标问题为: 最小化完成时间( ${C_{\max }}$ ), 最小化能耗总成本(TEC).

${C_{\max }}$ 为最后一批工件加工结束的时间, ${C_{\max }}$ 越小意味着机器的利用率越高. 在生产过程中使用随着时间变化的价格可能会给制造企业在成本上带来一定程度的节约, Nghiem等^[14]通过对减少峰值的能耗需求的控制系统的绿色调度进行研究, 并证明抑制峰值能够使成本和效率之间更加协调, 所以本文最小化TEC主要是通过延长 ${C_{\max }}$ 来降低能耗成本, 比如在用电高峰(单位电价较高)时等待或者关闭机器, 选择单位电价比较合理时(用电低峰)进行工件加工.

机器是否等待的判断标准是, 对比当前和后一单位时刻电价, 如果当前电价较低则不等待直接加工; 反之, 让机器处于待机状态或者关闭机器. $P{E_{\rm{idle}}}$ / $P{E_{\rm{on}}}$ / $P{E_{\rm{off}}}$ 分别为单位待机能耗/开机能耗/关机能耗, ${T_{\rm{idle}}}$ 、 ${T_{\rm{on}}}$ 、 ${T_{\rm{off}}}$ 为对应的时间, 用公式表示如下:

令上一批的完工时间为 ${t'} - 1$ , 如果满足条件公式(16), 则等待加工并计算等待时间 ${T_{\rm{idle}}}$ , 反之继续加工. 当等待时间为 ${T_{\rm{idle}}}$ 时, 如果满足条件公式(17), 则关闭机器, 反之等待加工.

$\left\{\begin{aligned}&{c_{{t'}}} \geqslant {c_{{t'} + 1}}\\&P{E_{\rm{idle}}}\sum\limits_{t = {t'}}^{t + {T_{\rm{idle}}}} {{c_t}} + {E^b}\sum\limits_{t = {t'} + {T_{\rm{idle}}}}^{t + {T^b}} {{c_t}} \leqslant {E^b}\sum\limits_{t = {t'}}^{t + {T^b}} {{c_t}}\end{aligned}\right. $

(16)

$\left\{\begin{aligned}&{T_{\rm{idle}}} \! \geqslant \! {T_{\rm{on}}}\! +\! {T_{\rm{off}}}\\&P{E_{\rm{idle}}}\sum\limits_{t \in {T_{\rm{idle}}}} {{c_t}} \!\geqslant\! P{E_{\rm{on}}}\!\! \sum\limits_{t \in {T_{\rm{on}}}} {{c_t}} \!+\! P{E_{\rm{off}}} \!\! \sum\limits_{t \in {T_{\rm{off}}}} {{c_t}}\end{aligned} \right.$

(17)

2.3 工件分批及其优化

本实验采用BF分批规则, 即工件 $j$ 放入的批次为满足机器容量要求且为当前加工时间最长的批.

在实验中引入一种左移调度, 即 $s{c^h}$ 是 ${B^h}$ 的剩余空间, ${P^h}$ 为 ${B^h}$ 的加工时间, ${B^h}$ 在 ${B^k}$ 前被加工, 如果 ${B^k}$ 中的工件 $i$ 满足 ${s_i} \leqslant s{c^h}$ 且 ${p_i} \leqslant {P^h}$ , 则从 ${B^k}$ 移到 ${B^h}$ 中, 直到 ${B^k}$ 中没有工件满足 ${s_i} \leqslant s{c^h}$ 且 ${p_i} \leqslant {P^h}$ , 大致过程描述如下:

(1) K为总批数, k=K.

(2) 如果k<2, 程序结束, 反之h=k-1.

(3) 如果 $h \geqslant 1$ , 找到 ${B^k}$ 中加工时间最长的工件a, 即 ${p_a} = {P^k}$ , ${B^h}$ 的剩余空间 $s{c^h}$ , ${B^k}$ 的剩余空间 $s{c^k}$ , 如果 ${p_a} > {P^h}$ , $h = h - 1$ ; 如果 ${p_a} \leqslant {P^h}$ 且 ${s_a} \leqslant s{c^h}$ , 把工件a从 ${B^k}$ 移到 ${B^h}$ 中, 更新批次; 如果 ${p_a} \leqslant {P^h}$ 且 ${s_a} \geqslant s{c^h}$ , 跳转(4). 反之k=k–1, 跳转(2).

(4) 找到 ${B^h}$ 中满足 ${p_i} < {p_a}$ 的工件集合 $\omega $ , $\omega= $ $ \{ i \in {B^h}|{p_i} < {p_a}\} $ , $\;\omega \in {B^h}$ 计算 $\omega $ 中所有工件的尺寸 $s(\omega )$ . 如果 ${B^k}$ 中工件a满足 $s(\omega ) \leqslant s{c^k} + {s_a}$ 且 ${s_a} \leqslant s{c^h} + s(\omega )$ , 工件a和集合 $\omega $ 中所有工件交换, 否则删除集合 $\omega $ 中最后一个工件直到集合 $\omega {\rm{ = }}\emptyset $ .

2.4 适应度的计算

如果 $C_{\max }^i \leqslant C_{\max }^j$ 且 $TE{C^i} \leqslant TE{C^j}$ , 而且至少有一个严格成立, 则个体i优于j, 表示为 $j \prec i$ , 个体j被个体 $i$ 所支配.

因为每个决策者对最大完成时间和能耗总成本的关注程度不一样, 所以引入偏好矩阵 $\omega {\rm{ = }}({\omega _c},{\omega _e})$ , 其中 ${\omega _c}$ 、 ${\omega _e}$ 分别表示完成时间和能耗总成本的权重, 且 ${\omega _c}{\rm{ + }}{\omega _e}{\rm{ = }}1$ , 它反映调度中对 ${C_{\max }}$ 和TEC的关注程度, 系数值越大表示关注程度越大. 令 $C_{\max }' = {\omega _c}{C_{\max }}$ , $TE{C'} = {\omega _e}TEC$ , 根据 $C_{\max }'$ 、 $TE{C'}$ 计算适应度, 结合文献[15]等使用的适应度计算方法, 本论文的适应度值表示为 ${F^i} = {S^i} + {d_i}$ , ${S^i}$ 和 ${d_i}$ 具体定义如下.

用 ${G^i}$ 表示个体 $i$ 优于其它个体的数目, 定义如下:

$\begin{aligned}&{G^i} = \sum\limits_{j = 1}^{PopSize} {{m_j}}\\&\left\{ {\begin{array}{*{20}{c}} {{m_j} = 1}&{j \prec i,i \ne j} \\ {{m_j} = 0}&{\rm{otherwise}} \end{array}} \right.\end{aligned}$

(18)

用 ${S^i}$ 表示严格优于自己的所有个体的长度值 ${G^i}$ 之和, 具体定义为:

${S^i} = \sum\limits_{j = 1}^{PopSize} {{G^j}} ,\;\;\forall i \prec j$

(19)

所以 ${S^i}$ 的值越大, 对应的个体越差, 因为它被其它更多个体所支配.

为了区分没有被其它解所支配的解的差异, 我们引入密度估计. 即根据 $C_{\max }'$ 、 $TE{C'}$ 计算欧式距离, 个体i, j之间的欧式距离定义如下:

${\omega _i} = \sqrt {{{\left( {C_{\max }^{'i} - C_{\max }^{'j}} \right)}^2} + {{(TE{C^{'i}} - TE{C^{'j}})}^2}} $

(20)

$\omega _i^k$ 为 ${\omega _i}$ 升序排列的第 $k$ 个值, $k = \sqrt {PopSize} $ , 密度估计定义为:

${d_i} = \frac{1}{{\omega _{_i}^k + 2}},\;\;0 < {d_i} < 1$

(21)

2.5 最优解的选择

决策者依据适应度值对目标值进行选择, 根据适应度值可以看出, 当适应度值越小代表个体越优.

本论文中采用优化的轮盘赌法与Metropolis准则相结合, 当一个种群被选中超过种群的20%需要对选择的个体进行修正, 主要是根据个体被选中的顺序对应原个体顺序来进行替换, 除了第一次出现的位置保持不变, 其它位置根据Metropolis规则来进行替换, 这样可以防止陷入僵局. 具体步骤如下:

(1) 对种群中的所有个体计算适应度值, 并将个体按从小到大的适应度值排列, 记为 ${S_1}$ .

(2) 根据选择概率轮盘赌选择个体, 并按选中的顺序排好序, 记为 ${S_2}$ .

(3) 根据 ${S_2}$ 的结果判断哪些个体被选中的次数超过种群的20%, 找到这些个体对应的原个体, 即对应位置上的 ${S_1}$ 中的个体, 除了第一次出现的位置不进行处理, 其余的位置通过Metropolis准则来判断该个体是被接受还是舍弃, 处理过程为:

1) i为 ${S_1}$ 中的个体, j为 ${S_2}$ 中对应位置的个体.

2) 当 ${F^i} > {F^j}$ , 产生随机数 $r \in (0,1)$ , 当满足条件 $r \leqslant \exp \{ ({F^j} - {F^i})/T\} $ 时, 保留 ${S_2}$ 中的个体j, 否则用个体i代替个体j, 其中T为控制参数.

3) 当 ${F^i} < {F^j}$ 时, 对 ${S_2}$ 中的个体j进行保留.

(4) ${S_2}$ 为最后选中的个体.

3 仿真实验与分析 3.1 实验设计

本实验采用文献[7]提出的随机产生方法获得算例, 算例的规模按如下4个标准进行划分: 工件数量 $N$ , 工件的加工时间 ${p_j}$ , 工件尺寸 ${s_j}$ , 工件加工功率 ${e_j}$ , 其中, ${p_j}$ , ${s_j}$ , ${e_j}$ 均服从离散均匀分布, 算例生成的若干参数及范围见表1.

为了对每类问题的算例进行标记, 用J1p1s1e1表示10个工件, 工件尺寸服从[1,10], 加工时间服从[1,10], 加工功率服从[3,5], 机器容量为10.

本文采用分时计价原则, 分时电价由电网的不同时期提供, 实验中采用夏季计价标准, 计价标准函数用 $c(t)$ 表示, 具体见公式(22), 表2和表3为与加工过程相关的信息.

$c(t) = \left\{ {\begin{array}{*{20}{c}} 5,&{24n - 3 \leqslant t < 24n + 7} \\ 8,&{24n + 7 \leqslant t < 24n + 11} \\ {10},&{24n + 11 \leqslant t < 24n + 17} \\ 8,&{24n + 17 \leqslant t < 24n + 21} \end{array}} \right.$

(22)

对于本论文的实验结果, 分别从解的质量和算法性能两方面进行比较.

(1)解的质量用Pareto最优解集规模表示, Pareto最优解集规模为找到非支配解的数量, 解的数目越多, 选择余地更多.

(2)用解集之间的覆盖率来对算法性能进行衡量, 覆盖率C(A,B)表示算法B所求得的Pareto最优解集被算法A所生成解集支配的解的比例, 按照下式计算:

$C{\kern 1pt} {\kern 1pt} (A,B) = \frac{{|\{ b \in B|\exists a \in A:a \succ b{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{or}}{\kern 1pt} {\kern 1pt} a = b\} |}}{{|B|}}$

(23)

其中, $a \succ b$ 表示解b被解a所支配. C(A,B)的值越接近1代表算法A的性能相对于算法B越好, 但一般情况下C(A,B) $ \ne $ C(B,A), 当C(A,B)>C(B,A)时表示算法A的性能优于算法B.

3.2 实验结果与分析

本实验中的算法均在Matlab 2016a平台下实现, 每类问题随机生成10个算例, 每个算例各运行15次取平均值.

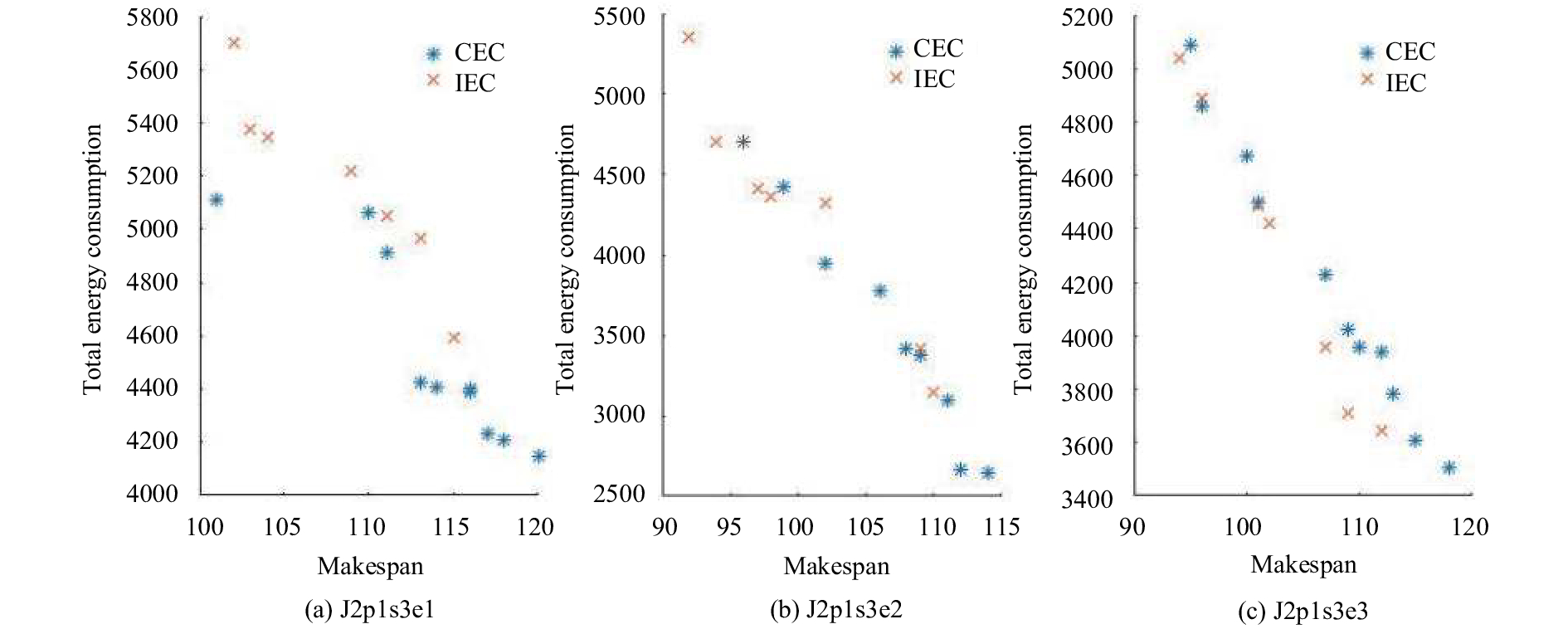
表4列出了在CEC和IEC下, 使用遗传算法在不同算例下找到的非支配解个数, 从表中可以看出, CEC找到的非支配解个数要明显优于IEC, 反映了在工件规模较大的情况下CEC对非支配解的搜索效果要优于IEC. 而且随着问题复杂程度的提高, 找到的非支配解个数呈现增加趋势.

表5列出了两种情况下在不同算例下找到的非支配解的质量对, 在J1类子问题中CEC的覆盖率和IEC的差不多, 但随着工件规模的增大, CEC的优势表现得更加明显, 说明在问题复杂度较高的情况下, CEC取得的非支配解在质量上要优于IEC.

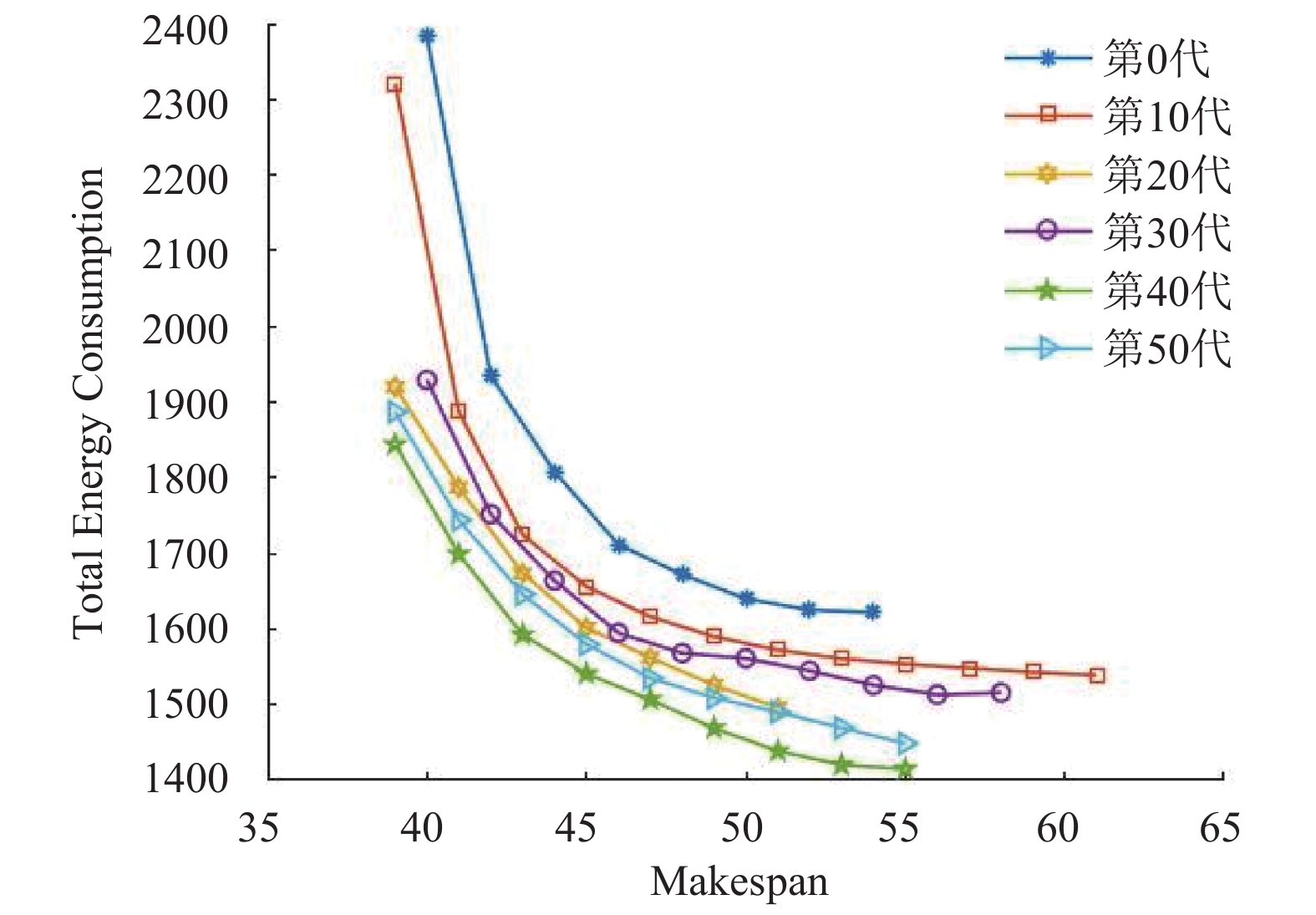
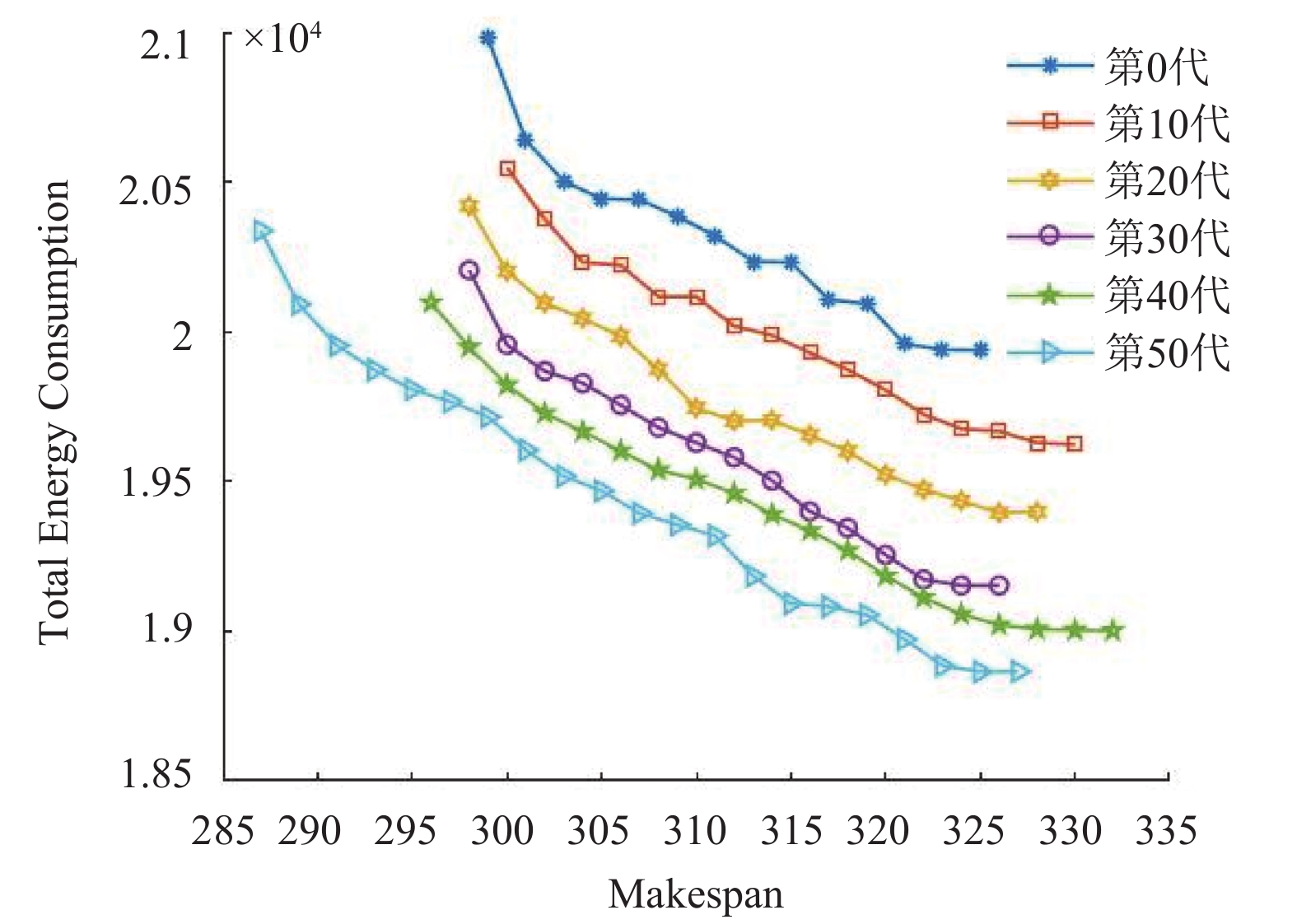
为了更形象化了解在不同情况下, 不同类型算例下非支配解的分布和算法的迭代优化情况, 下面绘制了算例的非支配解部分分布图和部分算例迭代寻优曲线.

4 结论

本文研究了遗传算法在考虑能耗的单机批调度中的应用, 目标为最小化最大完工时间和最小化能耗成本, 应用背景主要来源于眼镜生产过程中镜片的固化加热过程. 本文主要通过优化的遗传算法找到帕累托最优解, 在能耗成本计算中引入分时计价原则, 并利用偏好矩阵来对完工时间和能耗成本之间进行权衡, 同时结合非支配解来计算适应度值. 从实验结果来看, CEC下获得的解集规模更大. 另外, 对生产调度中的问题考虑能耗成本后可以在得到比较合理的完工时间的同时大大节约能耗成本, 这样更能满足实际生产过程中的需求.

这里还有很多方面可以在以后进行研究, 比如对机器状态转换过程的判断标准, 分时计价中的时间周期和定价标准的影响等问题进行进一步分析与研究. 另一方面可以想办法提高遗传算法对非支配解的搜索能力, 更好的求解双目标的差异工件单机批调度问题.