基于麦克风阵列的声源定位是利用麦克风阵列拾取多路声音信号, 结合声源和阵列结构之间的几何关系, 得到声源的位置信息. 由于麦克风阵列在时域和频域的基础上增加了空域信息, 因此对声音信息的处理能力明显增强[1]. 其优势主要体现于: 具有空间选择性、能够应用于声 源自动跟踪、能够识别同时发生的多个声源以及用于近场测距等.
目前的声源定位研究主要可分为二维空间定位与三维空间定位、近场定位与远场定位、方向定位与距离定位等几类. 其中, 基于到达时间差(Time Differences Of Arrival, TDOA)的声源定位算法在视频会议、车载导航、机器人、医疗诊断及海洋探测等领域的应用极为广泛[2–4]. 基于TDOA的定位方法是一种双步定位法. 该方法首先进行时延估计(Time Delay Estimation, TDE)估计声源信号到达麦克风对的时间差, 进而通过几何关系来确定声源的位置.
上世纪八十年代, Knapp和Carter[5]提出了利用互相关函数估计时延的广义互相关法(Generalized Cross Correlation, GCC), 将两路语音信号的互功率谱进行滤波后提取峰值作为时延估计值. GCC算法得到了广泛的应用, 而鉴于GCC算法受混响的影响较大, 一些学者对其做了改进, Champagne[6]提出的倒谱预滤波(CEpstral Prefiltering, CEP)技术先对信号进行预滤波, 有目的地去除信号中受混响影响较严重的部分, 再将预滤波后的信号通过GCC方法进行时间延迟估计; 此后, 又陆续出现了基于子空间分解的自适应特征值分解(Adaptive Eigenvalue Decomposition Algorithm, AEDA)[7]和基于声学传递函数比(Acoustic Transfer Functions ratio, ATF)[8]来进行时延估计的方法, 能够有效克服混响和噪声的影响.
1994年Omologo[9]提出了互功率谱相位 (Cross-power Spectrum Phase, CSP)算法. 这种方法对中低混响有很好的抑制作用, 吸引了一大批学者的关注, 有一些文献对其进行了改进, 出现了很多基于CSP算法的时延估计算法和应用场景[10–12]. 其中, 文献[13]提出了一种功率谱限幅后再进行反傅立叶变换的改进自相关方法. 采用相关峰跟踪搜索的方法实现了多径时延时间历程的自动提取, 这在无人系统中有较好应用前景. 文献[14]将时间细化逆傅里叶变换法应用到互功率谱相关算法中, 通过相关峰细化计算子带平移后互功率谱的相关函数, 并对各频带的峰值函数使用高斯函数进行尖锐化处理, 使得频带不重叠的多个不同声源的方位得以进行快速精确. 该方法解决了在小孔径、小阵元数接收基阵的情况下的多目标方位的精确快速估计问题, 适用于小孔径的探测节点与具有低功耗限制要求的平台使用. 文献[15]采用了互功率谱-平滑相干变换(CSP-SCOT)联合加权时延估计, 对声源进行空间搜索. 仿真实验结果表明, 在同等混响或噪声条件下, 此方法其定位优于CSP和SCOT算法, 且适于小型麦克风阵列.
相关函数法对于功率谱平坦的信号能取得良好性能, 在实际生活中, 许多噪声的功率谱都包含有较强线谱或窄带分量, 其性能急剧下降. 本文针对CSP算法在强混响与低信噪比环境下效果差的情况, 提出了一种改进的CSP算法. 算法主要针对时延估计错误的语音帧, 筛选出不合理的估计结果, 更新算法中的加权因子等参数后再次估计, 得到合理时延值并通过多帧加权平滑与麦克风校准的方式来提高算法的抗噪能力.
1 互功率谱相位算法对于由I个麦克风组成的阵列, 给定一个声源, 在理想环境下第i个麦克风在t时刻接收到的信号可表示为:
| ${x_i}(t) = {\alpha _i}s(t - {\tau _i}) + {v_i}(t) = {h_i}(t) * s(t) + {n_i}(t)$ | (1) |
其中, αi(αi<1)是声波传播的衰减系数,τi为声源到达第i个麦克风的传播时延, vi(t)表示加性噪声, 符号“*”为卷积运算, s(t)为声源信号, ni(t)为混响噪声.
显然, 麦克风阵列中的各阵元信号具有相关性. 第i、j个麦克风信号的互相关函数如下:
| ${R_{{x_i}{x_j}}}(\tau ) = E[{x_i}(t){x_j}(t - \tau )]$ | (2) |
其中,
假设噪声与声源信号不相关, 式(2)可简化为:
| ${R_{{x_i}{x_j}}}(\tau ) = {\alpha _i}{\alpha _j}{R_{{s_i}{s_j}}}(\tau - {\tau _{ij}}) + {R_{{v_i}{v_j}}}(\tau )$ | (3) |
其中,
由自相关函数的性质可知, 当τ-τij=0, 即τ=τij时,
这就表明, TDOA值可以从互相关函数峰值处得到. 但是在现实环境中, 声音会经过多次反射再次到达麦克风, 故麦克风接收到的语音信号由声源与噪声的直达波和反射波组成. 这些反射波的存在会形成伪峰, 严重影响时延估计的准确性(如图1所示).
CSP算法就是基于上述情况所提出来. 对式(3)做傅里叶变换得到xi(t)与xj(t)的互功率谱:
| ${P_{{X_i}{X_j}}}(\omega ) = {\alpha _i}{\alpha _j}{P_{{S_i}{S_j}}}(\omega ){e^{ - j\omega {\tau _{ij}}}} + {P_{{V_i}{V_j}}}(\omega )$ | (4) |
其中,
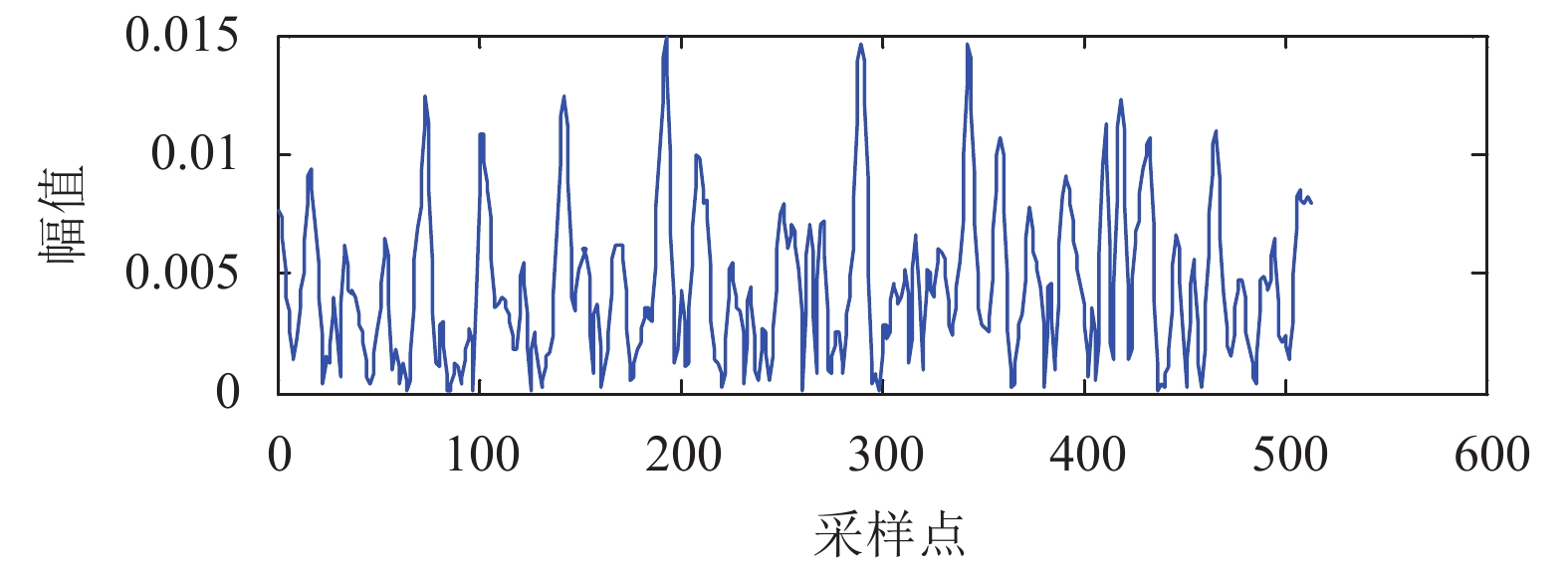
|
图 1 互相关函数的峰值被伪峰淹没 |
| ${R_{{\rm{csp}}}}(\tau ) = \int_{ - \infty }^\infty {\frac{1}{{\left| {{P_{{X_i}{X_j}}}(\omega )} \right|}}{P_{{X_i}{X_j}}}(\omega ){e^{i\omega \tau }}d\omega } $ | (5) |
其中,
| ${R_{m\_{\rm{csp}}}}(\tau ) = \int_{ - \infty }^\infty {\frac{1}{{{{\left| {{P_{{X_i}{X_j}}}(\omega )} \right|}^r}}}{P_{{X_i}{X_j}}}(\omega ){e^{i\omega \tau }}d\omega } $ | (6) |
CSP算法计算量小, 具备良好的跟踪计算能力, 适用于实时系统. 目前已经证明CSP算法在中等强度噪声、混响的环境下性能较好[18]. 但在实验过程中发现, 当处于低信噪比、高混响等复杂环境时, CSP算法准确率急剧下降, 误差明显增加. 本文的目的在于减少CSP算法在复杂环境下的错误率, 使其既满足于实时系统, 又能确保算法的准确性.
图2所示为本文所提算法的流程图. 由于语音信号的短时平稳性,首先对采集到的语音信号进行预处理, 得到语音发生段[B,E].
对[B,E]内的前M帧信号使用CSP算法估计时延, 得到第k(B<k<B+M)帧信号的时延值tdk(p)(p=1,2,3). 为提高CSP算法正确率, 判断tdk(p)是否处于合理时延区间[C1,C2](此区间由公式(12)计算得到)之间. 在此区间内的时延值予以通过, 反之, 更新加权因子r再次计算. 若2次更新后得到的时延值皆不在合理区间内, 则使用第一次计算得到的时延值tdk(1)与上一帧时延值τk-1加权作为当前帧的时延值τk. 依次得到M帧时延值τ1…τm, 最后对这M个时延值求均值, 作为此次声源的时延值τ.
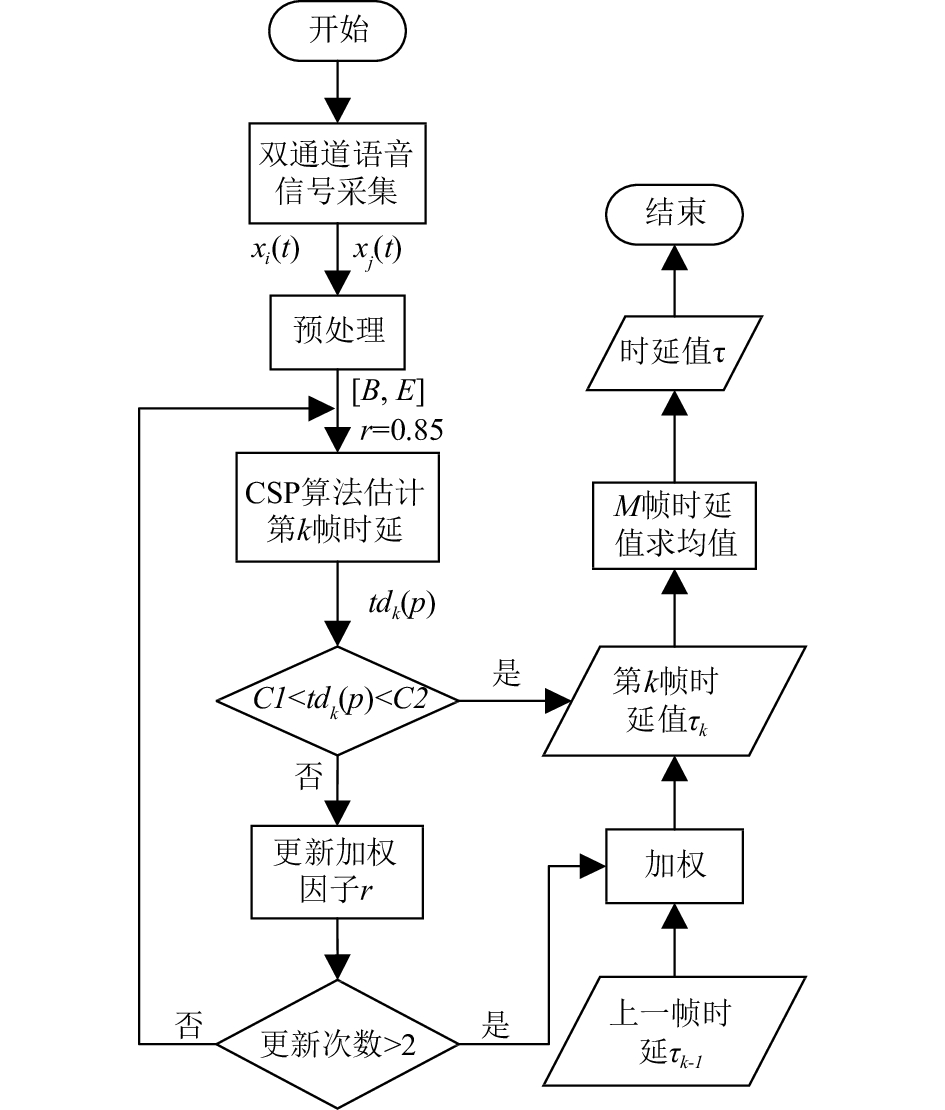
|
图 2 改进CSP算法流程图 |
2.1 预处理
本文对语音信号的预处理包括归一化、分帧、加窗、端点检测(Voice Activity Detection, VAD)等几个步骤.
首先将双通道语音信号进行归一化处理, 归一化后样本数据数值范围是[–1,1]. 然后, 对归一化的数据进行分帧、加窗处理, 用于减小语音截断误差, 其中, 帧长为512, 帧移为64, 窗类型为汉明窗. 最后, 对分帧加窗后的语音信号进行端点检测, 以降低算法运算量. 端点检测后分别得到语音开始帧、结束帧以及语音发生段[B,E], 如图3所示, 当B1=B2时, B=B1=B2; 当B1≠B2时, B=max(B1,B2). 同理, 当E1=E2时, E=E1=E2; 当E1≠E2时, E=min(E1,E2).
2.2 合理时延区间计算当语音混有强噪声、强混响时, 互功率谱函数的计算受噪声和混响的影响出现误差, 进而影响峰值检测. 为了减少错误的时延估计值, 降低无效的计算量, 我们引入一个合理时延区间, 对所有无效时延进行剔除, 从而提高算法计算效率与时延精度.
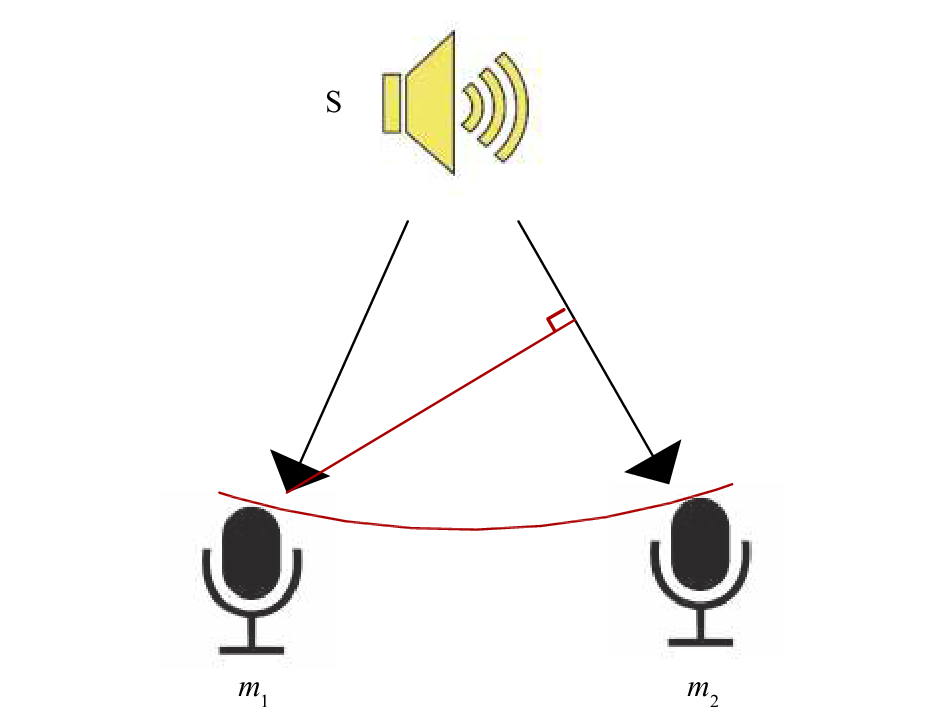
如图4示, 设声源S到麦克风m2的夹角为θ, 麦克风m1与m2间的距离为d12, 有:
| $\cos \theta = \frac{{{l_{e{m_2}}}}}{{{d_{12}}}}$ | (7) |
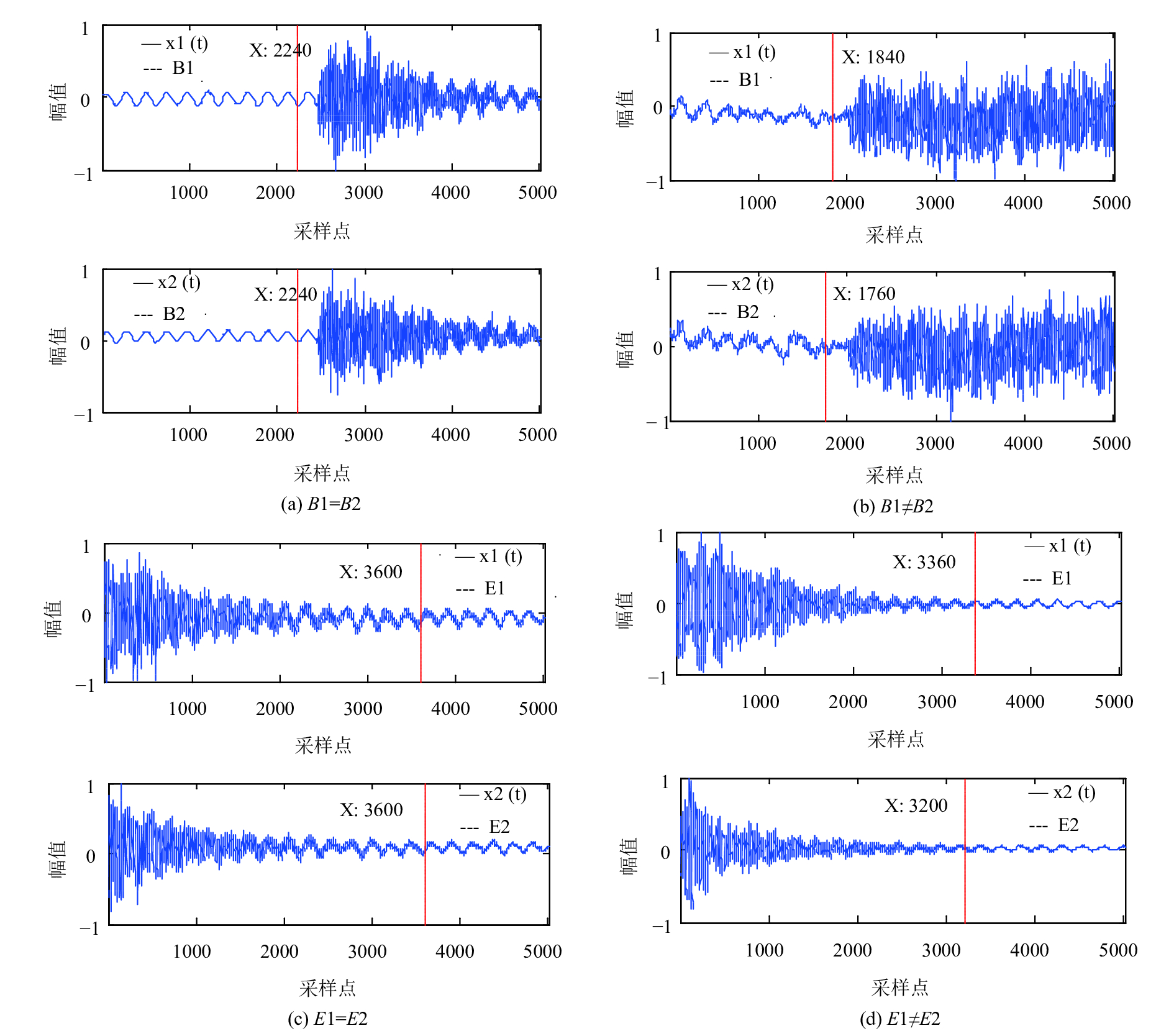
|
图 3 VAD语音发生段检测 |
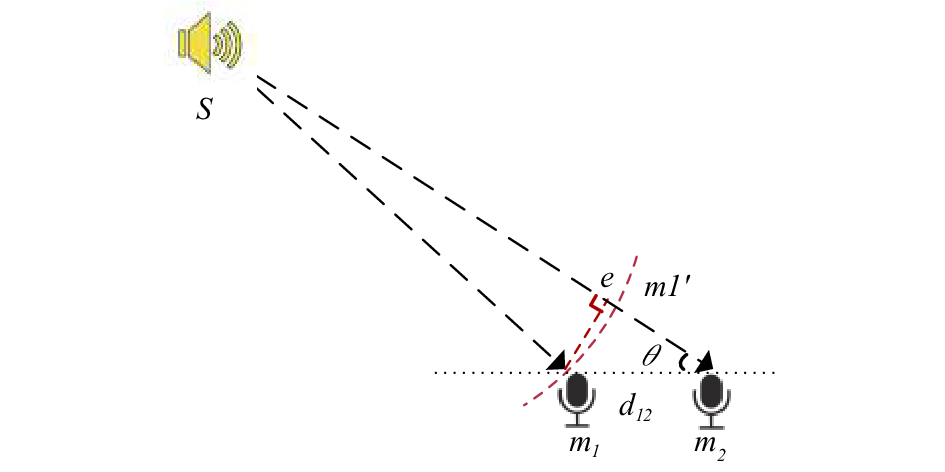
|
图 4 声源到两路麦克风信号 |
其中, e为从麦克风m1向Sm2作垂线的交点,
一般情况下, 声源S到麦克风阵列的距离远大于阵列孔距d12. 因此, 用曲线m1’m2近似代替直线m1e, 式(7)可化为:
| $\cos \theta \approx \frac{{{l_{{m_1}'{m_2}}}}}{{{d_{12}}}} = \frac{{\tau \cdot c}}{{{d_{12}}}}$ | (8) |
其中,
为了方便表示, 用采样点数N来表示时延的大小, N与τ的关系为:
| $N = \tau \cdot Fs$ | (9) |
其中, Fs为采样频率.
将式(9)带入式(8), 且由-1≤cosθ≤1可得:
| $ - \frac{{{d_{12}} \cdot Fs}}{c} \le N \le \frac{{{d_{12}} \cdot Fs}}{c}$ | (10) |
考虑到由曲线m1’m2代替直线m1e的误差, 当声源与麦克风阵列距离越近时误差越大. 由于阵列孔距较小, 忽略声源与麦克风阵列的距离小于孔距等极少数情况. 当声源到麦克风阵列距离与阵列孔距相等时, 如图5所示, 误差达到极大值, 此时误差距离为孔距d12的二分之一.
|
图 5 近场误差 |
则更新式(10)为:
| $ - \frac{{3{d_{12}} \cdot Fs}}{{2c}} \le N \le \frac{{3{d_{12}} \cdot Fs}}{{2c}}$ | (11) |
由此得到合理时延区间[C1,C2], 其中C1=–3d12·Fs/2c, C2=3d12·Fs/2c.
2.3 更新加权因子CSP算法中加权因子r(0.5≤r≤1)的选取极为重要. r值过大会使噪声过滤效果很差, r值过小又会过度加权, 造成峰值检测不正确. 一般来说, r的大小由经验决定. 为了确定本文改进算法中r的有效值, 本文对100组不同信噪比的语音信号进行了分析与统计. 对每组语音信号分别计算r为0.65、0.70、0.75、0.80、0.85、0.90、0.95、1时的时延结果, 并与真实时延对比, 记录下最为接近真实值的估计结果对应的r值. 获得最多次最小误差的r值即为最佳加权因子, 统计结果表1所示.
| 表 1 不同r值取得最小误差的次数 |
表1中为各r值的估计结果与真实值最接近的次数. 从图中可以看出, r=0.85时取得最小误差的次数最多, 明显高于其他值. 0.80与0.70次之, 分别排在第二位与第三位. 故本文使用0.85作为加权因子r的初始值、0.80和0.70为更新值.
2.3 多帧信号加权CSP算法只需要一帧语音信号就可以估计出时延, 但VAD算法参数的变化使检测到的语音发生段[B,E]可能不同. 为了减少VAD算法及噪声对时延估计结果的影响, 本文使用多帧时延加权平均的方法来提高算法的鲁棒性, 即对语音发声段内的前M帧信号取均值.
M的取值是我们要考虑的问题. M太小, 帧数太少达不到加权的效果; M太大又会降低算法执行效率. 为了得到合理的M值, 本文通过对100组语音信号进行计算, 得到M等于5时效果最佳. 由此可得语音信号的时延值τ为:
| $\tau = ({\tau _1} + {\tau _2} + {\tau _3} + {\tau _4} + {\tau _5})/5$ | (12) |
其中, τ1, …, τ5分别为语音发生段前5帧信号的时延.
3 实验分析为了验证本文所提算法的有效性, 本文分别进行了仿真实验与真实实验.
3.1 MATLAB仿真实验首先仿真真实房间合成不同信噪比的带噪语音信号, 再同时对这些语音信号使用经典CSP算法和本文改进算法完成时延估计, 并对两者的估计结果进行对比分析.
本文使用镜像源方法[19]仿真房间脉冲响应函数, 再结合噪声位置合成信噪比分别为0 db、5 db、10 db、15 db与20 db的带噪语音信号. 对这些信号分别使用本文改进算法与经典CSP算法估计时延, 实验中声源时延为2.88, 设算法估计结果ND与2.88相差超过1为错误估计, 即: 当|ND–2.88|≤1为正确估计, 当|ND–2.88|>1为错误估计. 结果如表2所示.
| 表 2 算法改进前后正确率(%) |
由表2可以看出, 传统CSP算法在高信噪比环境下正确率较高, 一些组甚至超过了90%; 但在低信噪比环境下正确率大大下降, 例如0 db时算法正确率只有58%. 相较于传统CSP 算法, 本文改进算法在各信噪比环境下正确率皆有提升. 在10 db、15 db和20 db等较高信噪比环境下的正确率达到95%以上; 而对5 db、0 db等低信噪比环境下分别提高了16%与21%, 平均达到了较高的算法正确率.
3.2 真实实验通过Matlab仿真初步验证了本文改进算法的有效性, 下面将进一步验证算法在真实语音环境下的效果. 首先, 使用双通道麦克风阵列在真实房间内采集了250组语音信号, 分别使用CSP算法与本文改进算法进行分析. 其次, 计算麦克风阵列的误差函数, 通过麦克风阵列误差的消除进一步提升算法正确率.
3.2.1 信号采集本文使用北京东方噪声技术研究所研发的录音设备与录音软件进行实时录制, 录音设备和软件如图6所示.

|
图 6 信号采集设备 |
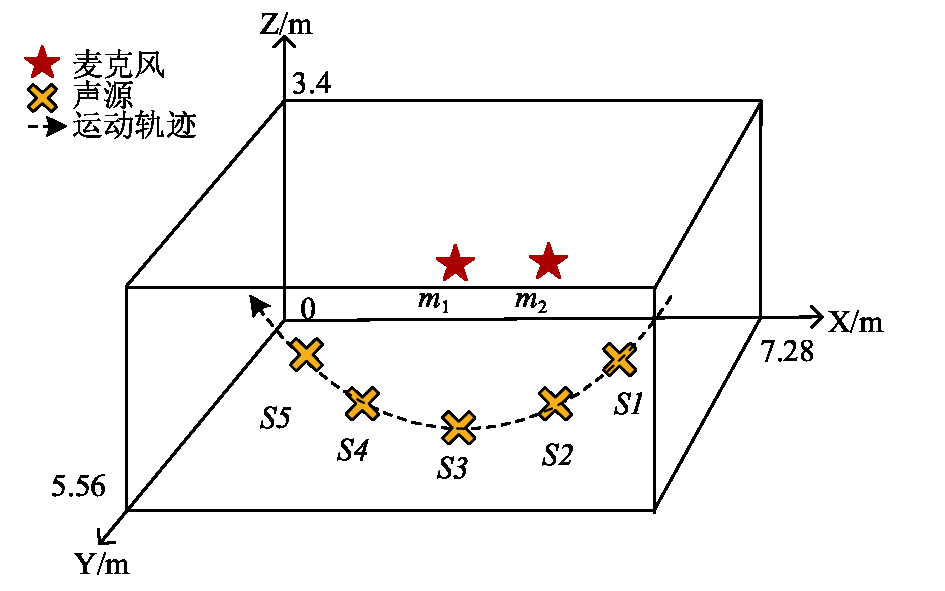
实验使用双通道直线型麦克风矩阵, 麦克风间距0.6 m, 阵列距地面75 cm. 实验室房间长7.28 m, 宽5.56 m, 高3.4 m. 以房间左上角建立三维坐标, 麦克风m1、m2坐标分别为(3,0.6,0.75)与(3.6,0.6,0.75).
受试者首先站在靠近麦克风m2的角落处, 当录音开始时, 实验者从麦克风m2向麦克风m1方向处走动, 并在过程中, 在设定好的位置S1至S5处拍手(这些位置分别位于麦克风阵列的π/6、π/3、π/2、2π/3、5π/6处), 走完一圈为一组语音信号, 重复录制250遍, 共得到250组语音信号. 录制过程如图7所示.
|
图 7 信号采集模型 |
3.2.2 麦克风校准
较之仿真室内环境, 真实房间的声学环境更为复杂. 除了环境噪声、室内混响等因素外, 房间大小、窗帘和桌椅等室内布置和受试者身体遮挡等许多因素会影响麦克风定位的精度. 因此, 对于不同的房间, 在定位之前应进行麦克风校准工作, 以降低房间变化带来的定位误差. 本文在安静环境下录制语音信号进行定位实验, 并与预设的声源实际角度进行比较, 得到麦克风阵列误差值.
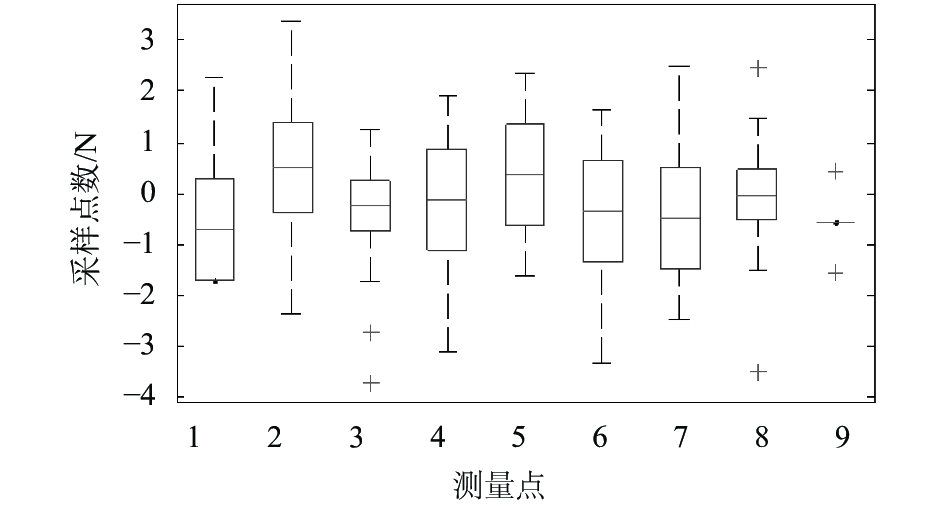
实验设计如下: 选择夜晚等安静时间, 紧闭实验室门窗、清空实验室中阻碍声音传播的物体; 在以麦克风阵列为中心的0—π/2扇形区域内每隔π/9设置一个测量点, 共计9个测量点; 受试者从第一个测量点依次走到第9个测量点并在每个测量点拍手完成一次录制. 重复录制30次, 得到30组双通道语音信号.
|
图 8 麦克风阵列误差校准 |
使用本文改进算法对上述30组双通道语音信号计算时延, 与实际值比较得到麦克风阵列误差值, 如图8所示. 利用Matlab中plotfit函数对误差均值拟合得到误差函数, 并由麦克风阵列的对称性可得0—π内的麦克风阵列误差函数.
3.2.3 实验结果对上述采集到的250组语音信号分别使用CSP算法、本文改进算法和经过麦克风校准后的本文改进CSP算法进行时延估计, 设算法估计结果ND与真实值之差的绝对值大于1即为错误估计. 分别记录下三种情况的算法错误率, 如表3所示.
| 表 3 算法改进前后错误率(%) |
表3可以看出, 改进后CSP算法的错误率比改进前有明显降低, 而经过麦克风校准的改进算法错误率比之又有下降. 不同角度的算法错误率各不相同, π但无论算法改进前后, 在接近π/2时错误率最低, 而接近0与π的两端角度则错误率较大. 改进后算法每组的错误率均有降低, 其中5π/6组错误率下降最多, 达到11.2%的提升效果; π/2组在改进后只有3.2%的错误率, 拥有极高的算法精度. 经过对麦克风阵列校准后的改进CSP算法比未经校准的算法正确率有提升, 其中错误率最大的一组为π/6组的4.1%, 最小的π/2组则只有1.3%. 相比于经典CSP算法, 麦克风校准后的改进CSP 算法平均降低了10.2%的错误率, 其中5π/6组甚至降低了15.3%, 大大提升了算法正确率, 实验结果表明本文所提改进CSP算法的有效性.
4 结束语本文针对CSP算法在低信噪比语音环境下算法错误率大的情况, 提出了剔除错误估计来提高正确率的改进算法. 首先通过语音环境和麦克风阵列信息计算出麦克风阵列误差函数、合理时延区间和最佳加权因子等. 其次使用CSP算法估计时延, 挑出不在合理时延区间内的估计值, 改变加权因子等参数后再次估计. 若重复2次估计后的时延值均不合理, 则利用前一帧时延值与第一次时延估计值加权作为当前帧的时延值. 最后消去麦克风阵列误差并利用5帧时延平滑得到此声源的时延估计, 进而得出声源位置信息. 通过语音仿真实验与真实环境下录制的语音信号实验皆验证了本文改进算法的有效性, 改进后算法正确率较改进前平均提高了10.2%, 改善了CSP算法在复杂语音环境下的算法精度, 提高了CSP算法的正确率与鲁棒性.
| [1] |
陶巍, 刘建平, 张一闻. 基于麦克风阵列的声源定位系统. 计算机应用, 2012, 32(5): 1457-1459. |
| [2] |
Magassouba A, Bertin N, Chaumette F. First applications of sound-based control on a mobile robot equipped with two microphones. Proceedings of 2016 IEEE International Conference on Robotics and Automation. Stockholm, Sweden. 2016. 2557–2562.
|
| [3] |
Jang Y, Kim J, Kim J. The development of the vehicle sound source localization system. Proceedings of 2015 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, Hong Kong, China. 2016. 1241–1244.
|
| [4] |
Hirano Y, Iwai T, Kominami D, et al. Implementation of a sound-source localization method for calling frog in an outdoor environment using a wireless sensor network. Proceedings of 2016 International Conference on Wireless Communications, Signal Processing and Networking. Chennai, India. 2016. 2458–2462.
|
| [5] |
Knapp C, Carter G. The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976, 24(4): 320-327. DOI:10.1109/TASSP.1976.1162830 |
| [6] |
Stéphenne A, Champagne B. A new cepstral prefiltering technique for estimating time delay under reverberant conditions. Signal Processing, 1997, 59(3): 253-266. DOI:10.1016/S0165-1684(97)00051-0 |
| [7] |
Benesty J. Adaptive eigenvalue decomposition algorithm for passive acoustic source localization. The Journal of the Acoustical Society of America, 2000, 107(1): 384-391. DOI:10.1121/1.428310 |
| [8] |
Dvorkind TG, Gannot S. Time difference of arrival estimation of speech source in a noisy and reverberant environment. Signal Processing, 2005, 85(1): 177-204. DOI:10.1016/j.sigpro.2004.09.014 |
| [9] |
Omologo M, Svaizer P. Acoustic event localization using a crosspower-spectrum phase based technique. Proceedings of 1994 IEEE International Conference on Acoustics, Speech, and Signal Processing. Adelaide, SA, Australia. 1994. II/273–II/276.
|
| [10] |
Kou WZ, Duan WJ, Li MY. An improved time delay estimation method based on cross-power spectrum phase. Proceedings of 2012 IEEE International Conference on Signal Processing, Communication and Computing. Hong Kong, China. 2012. 686–690.
|
| [11] |
Zhou WZ, Ling Y, Zhang YQ, et al. Time difference calculation based on signal starting point detection. Proceedings of the 2015 7th International Conference on Modelling, Identification and Control. Sousse, Tunisia. 2015. 1–5.
|
| [12] |
Mao HD, Zhang LH. An improved accumulated cross-power spectrum phase method for time delay estimation. Proceedings of 2015 IEEE Advanced Information Technology, Electronic and Automation Control Conference Chongqing, China. 2015. 563–566.
|
| [13] |
陈韶华, 汪小亚. 一种改进的自相关多径时延估计及其自动提取. 中国声学学会第十一届青年学术会议会议论文集. 西安. 2015.
|
| [14] |
刘超, 黄迪. 基于子带平移的精确时延快速估计. 舰船电子工程, 2016, 36(6): 127-130. DOI:10.3969/j.issn.1672-9730.2016.06.034 |
| [15] |
杨艺敏, 刘涛. 改进的GCC算法在声源定位中的研究. 电子世界, 2017(10): 180, 186. |
| [16] |
崔玮玮. 基于麦克风阵列的声源定位与语音增强方法研究[博士学位论文]. 北京: 清华大学, 2009.
|
| [17] |
Rabinkin DV, Renomeron RJ, Dahl AJ, et al. DSP implementation of source location using microphone arrays. Journal of the Acoustical Society of America, 1996, 99(4): 88-99. |
| [18] |
陆晓燕. 基于麦克风阵列实现声源定位[硕士学位论文]. 大连: 大连理工大学, 2003.
|
| [19] |
Fu ZH, Li JW. GPU-Based Image Method For Room Impulse Response Calculation. Hingham, MA, USA: Kluwer Academic Publishers, 2016.
|
 2018, Vol. 27
2018, Vol. 27


