2. 山西大同大学 教育科学与技术学院, 大同 037009;
3. 山西大同大学 网络信息中心, 大同 037009
2. School of Education Science and Technology, Shanxi Datong University, Datong 037009, China;
3. Network Information Center, Shanxi Datong University, Datong 037009, China
在计算机辅助设计(Computer Aided Design, CAD)软件中, 用户一般在模型空间绘制图形, 在布局空间打印出图. 由于工程图需要从不同角度综合反映工程模型的空间尺寸和几何关系, 例如主视图、左侧图、俯视图、局部详图等[1,2]. 在打印出图时, 需要输出模型空间所绘图形的不同视图. 在CAD软件的布局空间中, 可以将任意闭合区域作为裁剪边界(视口)输出图形, 用户只关注视口内部的图形[3–6]. 当批量执行矢量图形的裁剪时, 裁剪算法的优劣直接影响着工程图形的生成效率.
1 矢量图形在非自交多边形边界中的裁剪矢量图形是使用直线和曲线来描述的图形, 用户视窗一般都为多边形. 当需要裁剪掉用户视窗外的图形时, 其本质就是直线或圆这两种图形和多边形相交时, 裁剪掉多边形外边的直线或圆的部分[7].
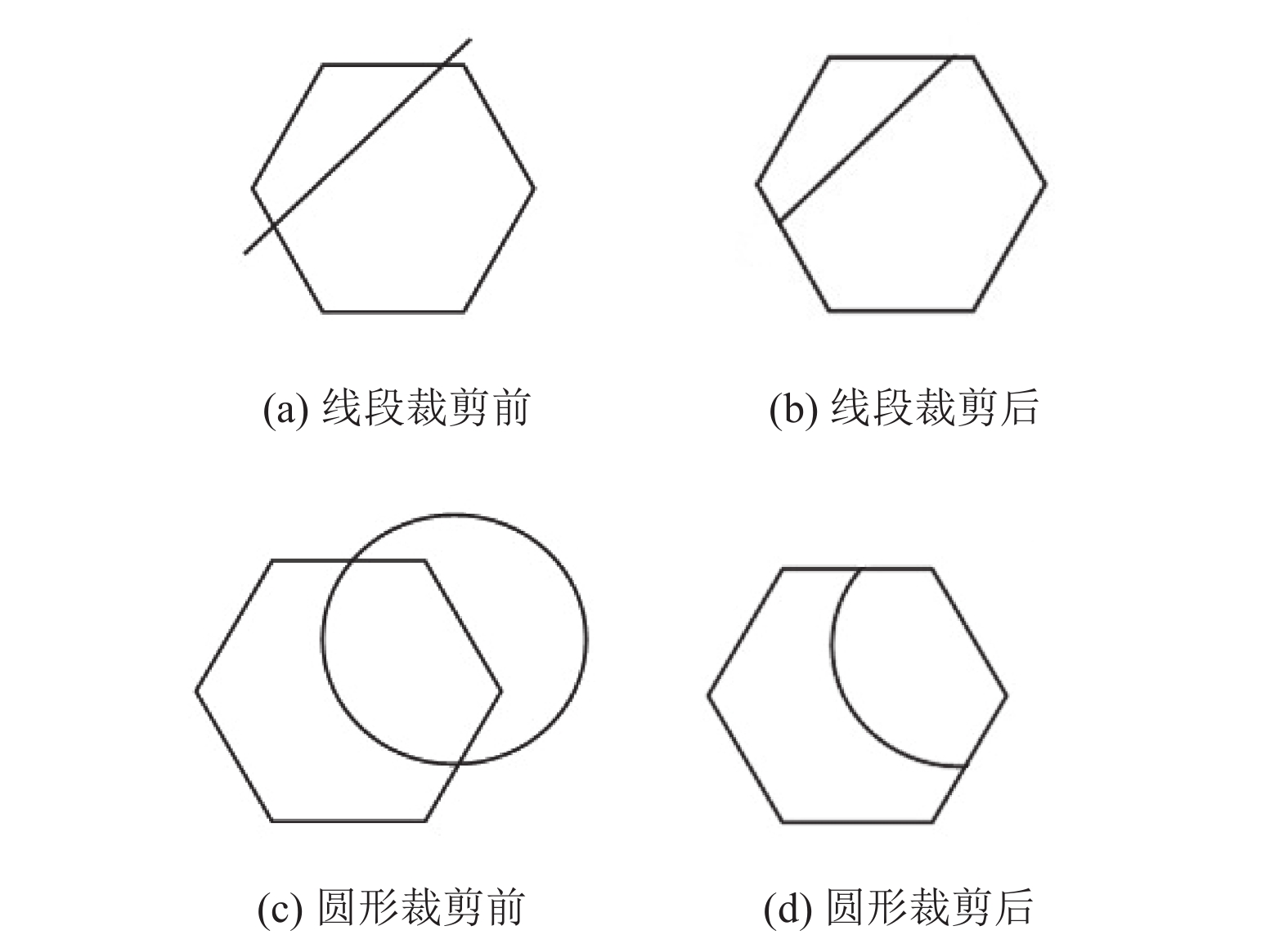
任意线段和圆, 与凸多边形裁剪边界相交时能够正确裁剪的显示. 图形在裁剪边界外的部分不显示, 在裁剪边界内的部分正确显示, 如图1所示.
|
图 1 线段、圆与凸多边形裁剪 |
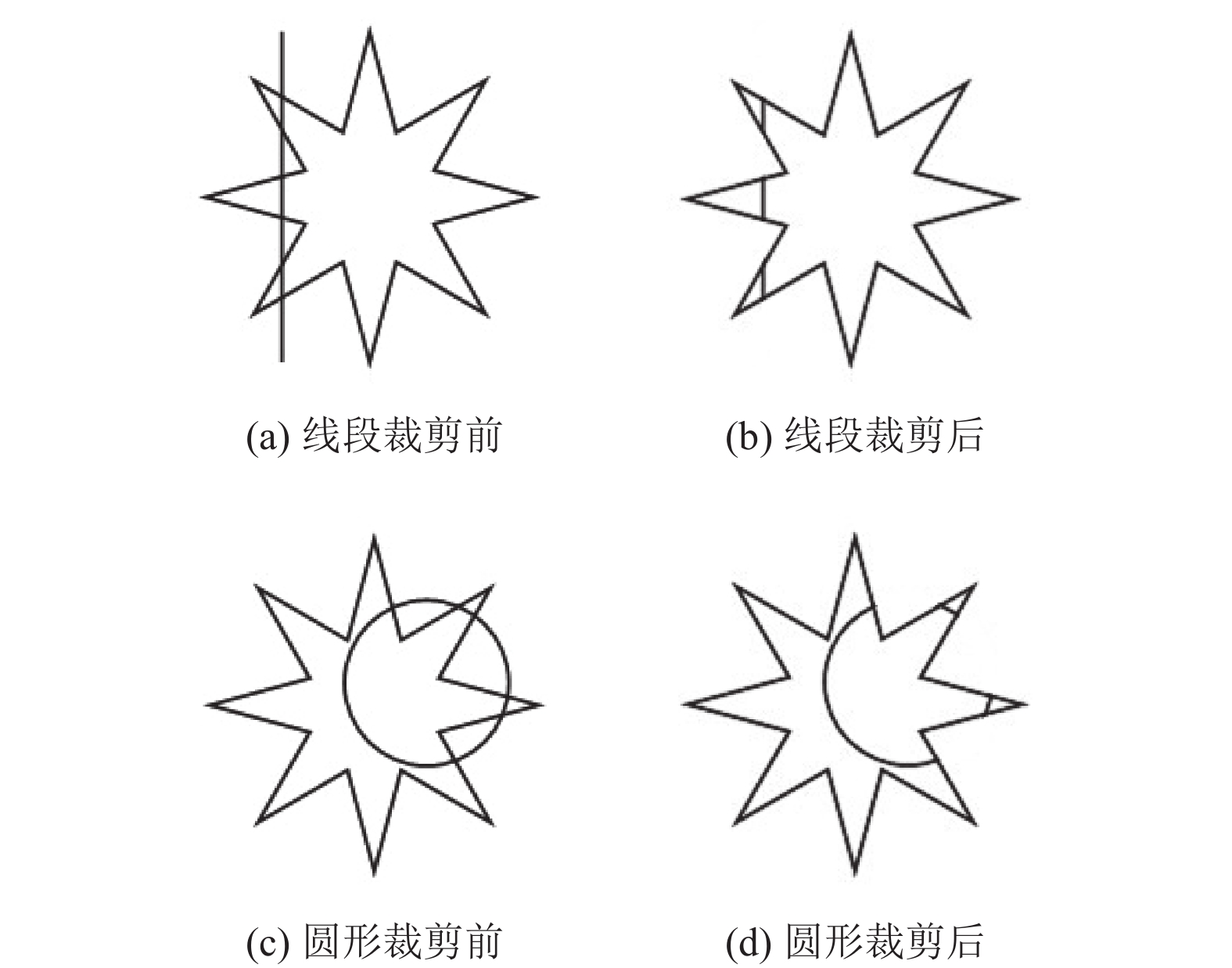
任意线段和圆, 与凹多边形裁剪边界相交并且跨凹多边形的优角时能够正确裁剪的显示. 图形在裁剪边界外的部分不显示, 在裁剪边界内的部分正确显示, 如图2所示.
|
图 2 线段、圆与凹多边形裁剪 |
2 矢量图形在非自交多边形边界中裁剪的传统算法 2.1 线段裁剪非自交多边形传统算法思路
线段与多边形裁剪算法的基本思路是通过遍历多边形的每条边使其分解为求线段与线段的交点, 利用直线的一般方程求解时, 得到的交点可能是线段与线段的交点也有可能是直线与直线的交点即所求解的交点位于线段的延长线上, 为了避免无效交点求解过程中时间和内存的消耗, 在求解交点之前进行判断, 通过快速排斥实验和跨立实验筛选有交点的线段并求解交点, 利用列表对其进行存储[8,9]. 对列表中的点进行排序, 并通过依次遍历列表中两个点, 如果中点在多边形内部则进行绘制, 否则不绘制.
2.2 圆裁剪非自交多边形传统算法思路圆相对于多边形裁剪的关键是求出圆和多边形每条边的交点. 首先通过依次遍历多边形的每条边将其分解为线段与圆的交点, 为了排除直线斜率的影响采用直线的一般方程:
在循环过程中如果使用j<TestCase.circles.size(), 会在每一次循环过程中重复计算, 造成不必要的冗余[10,11]. 在循环之前采用变量接收的方式, 避免多次计算.
(1) 直线中交点求解冗余
先判断直线与多边形的边是否有交点, 当存在交点的情况再对要裁剪的线段求解方程所需要的变量, 如斜率和偏移量; 否则, 不进行计算, 直接跳出本次循环.
(2) 圆中交点求解冗余
在传统的圆的求解交点算法中对多边形某条边线段变量A、B、C等的求解会在每一次的循环中进行求解即使圆与线段无交点的情况下也会冗余进行[12]. 解决方法:将这些变量的求解放到d(圆心到线段的距离)<=R(半径)的判断当中, 减少了当不存在交点的情况的求解, 减少时间消耗.
3.1.2 重用对象在传统算法中, 对于需要裁剪的每一条线段的端点记录都在每次循环时进行重新新建, 需要不断的在堆内存中开辟引用空间, 浪费时间还浪费内存的消耗.改进算法定义一个函数的局部变量, 开辟两个Point点堆内存空间, 利用set和get方法对两个Point对象进行重新设置, 以减少内存和时间的消耗.
3.1.3 多线程控制分别对直线裁剪、圆裁剪增加多线程. 从直线、圆裁剪数量的一半进行划分, 分别使用两个线程同时进行裁剪绘制. 同时避免公用对象Graphics2D g2的混合使用.
3.2 线段裁剪非自交多边形改进算法裁剪算法的描述如下:
Step 1. 用int nPoints变量存储多边形的顶点数量, 利用两个一维整型数组分别存储点的x, y坐标, 实现二维数组的功能, 并且设置标志量flag1、flag2为true.
Step 2. 获取一条线段, 判断斜率是否存在, 如果不存在设置标志量flag2=false; 如果存在求解线段的斜率k2和b2.
Step 3. 依次遍历多边形的每条边, 在每一次循环之前都将上一次用于存储线段和多边形的交点以及在多边形内部线段的顶点的列表plist清空, 并且获取当前线段的坐标封装在类Line的对象line中.
Step 4. 判断斜率是否存在, 如果不存在设置标志量flag1=false; 如果存在求解该线段的k1, b1.
Step 5. 判断所获取的两条线段是否有交点, 如果无交点转Step 11; 如果有交点转Step 6.
Step 6. 如果(!flag1&&!flag2)或(k1==k2&&flag1&&flag2)跳出本次循环, 转Step 3; 否则求解交点坐标.
Step 7. 当所求交点坐标中不含有该点, 则将交点存储在列表中, 否则不作处理, 转Step 3进行下轮循环, 直到多边形的每条边都被遍历完转Step 8.
Step 8. 分别判断线段的两个端点是否在多边形内部, 如果在则存入列表中, 不再不作处理, 转Step 2直到所有的线段都被求解完转Step 9.
Step 9. 对列表中的点进行排序.
Step 10. 依次遍历列表中的点, 判断两点的中点坐标是否在多边形内部, 如果在则进行绘制; 否则不进行处理.
Step 11. 结束.
3.3 圆裁剪非自交多边形改进算法对于中点坐标的求解采用Arc2D中弧线的类直接求中点坐标.
(1) 多边形某条边(线段)与圆求交点的算法思路
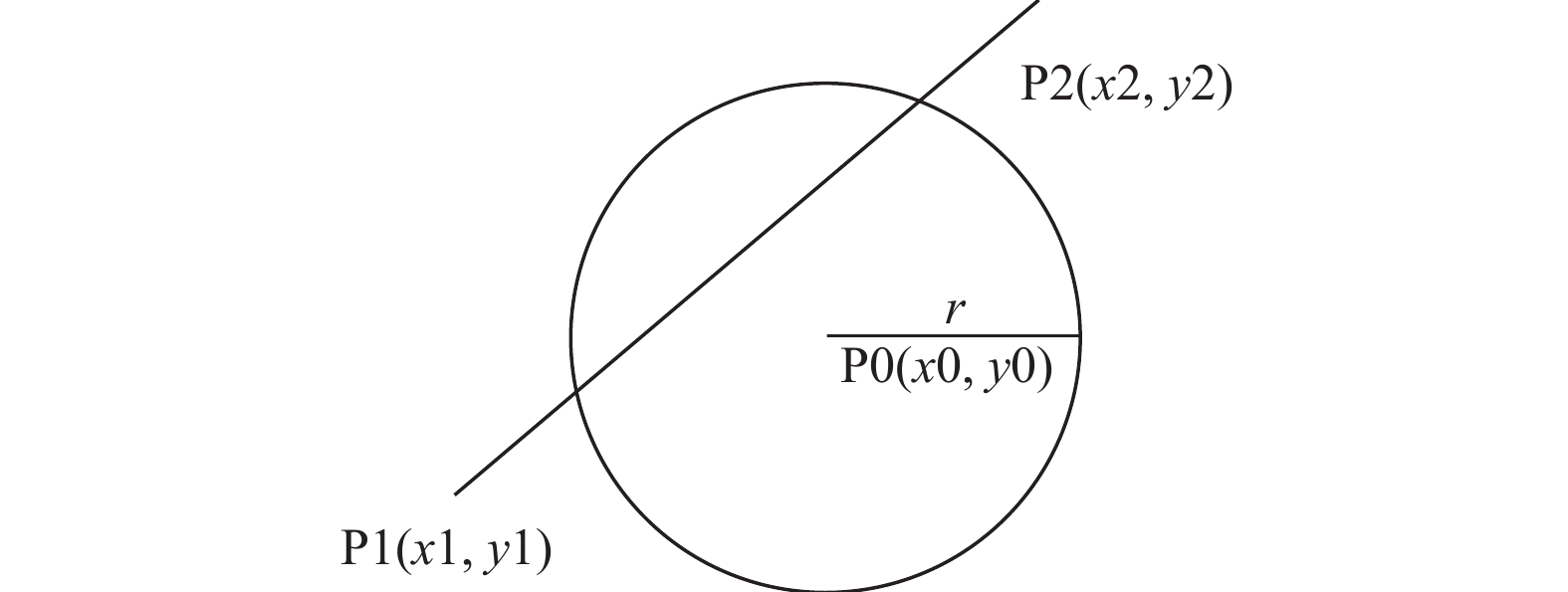
已知线段P1P2, 端点坐标为P1(x1, y1), P2(x2, y2), 如图3所示. 则其方程为:
| ${{a}}x + {{b}}y + {{c}} = 0$ | (1) |
其中,
圆的方程为:
| ${\left( {x - {{x}}0} \right)^2} + {\left( {y - {{y}}0} \right)^2} = {{{r}}^2}$ | (2) |
|
图 3 线段与圆求交点 |
由求点到直线的距离方法radiusTolines, 可得到圆心(x0, y0)到P1P2的距离d. 若d>r, 则表明线段与圆没有交点, 否则, 讨论交点求法.
P1P2的参数方程为:
| $\left\{\begin{array}{l}x = {{x1 + (x2}} - {{x1)}}t\\y = {{y}}1 + ({{y}}2 - {{y}}1)t,\;\;t \in \left[ {0,1} \right]\end{array}\right.$ | (3) |
将(3)代入(2)中, 化简整理得:
| ${{A}}*{t^2} + {{B}}*t + {{C}} = 0$ | (4) |
其中,
| $\left\{\begin{array}{l}{{A = x}}{{\rm{1}}^{\rm{2}}}{{ + x}}{{\rm{2}}^{\rm{2}}}{{ + y}}{{\rm{1}}^{\rm{2}}}{{ + y}}{{\rm{2}}^{\rm{2}}}{{ - 2*x1*x2 - 2*y1*y2}}\\{{B = 2}}({{x0*x1 + x1*x2 + y0*y1 }}\\\;\;\;\;\;\;+{{y1*y2 - x0*x2 - y0*y2 - x12 - y12}}) \\{{C = x}}{{\rm{0}}^{\rm{2}}}{{ + x}}{{\rm{1}}^{\rm{2}}}{{ + y}}{{\rm{0}}^{\rm{2}}}{{ + y}}{{\rm{1}}^{\rm{2}}}{{ - 2*x0*x1 - 2*y0*y1 - }}{{{r}}^{\rm{2}}}\end{array}\right.$ |
令
(2) 圆与多边形交点的排序算法
以圆心为原点, 以圆心左右两边区分所有交点, 按照顺时针方向进行排序. 设圆心坐标为p(x0, y0), 其他点坐标为(x, y), 由于可执行程序已经进行坐标点的转换, 所以使得原点为框体右上角的顶点, 向下为y值增大方向分为2种情况:
①
②
(3) 判断圆弧是否裁剪的算法
设Q1, Q2,…, Qk是多边形与被裁减圆的所有交点, 并且进行顺时针方向排序. 对两相邻的交点Qi, Qi+1(
根据Java中Arc2D的弧线类, 通过Qi, Qi+1确定需要绘制的弧线参数, 通过类中方法, 返回两个点的夹角, 并再次通过一个弧线类的对象, 设置起始点和夹角来确定弧线的中点坐标M3;
① 若M3在窗口外, 圆弧QiQi+1被裁剪.
② 若M3在窗口内, 圆弧QiQi+1被保留.
4 系统仿真实验及分析为了更进一步验证“矢量图形在非自交多边形边界中裁剪的算法”正确性和算法的执行效率、内存消耗等问题, 模拟CAD软件的布局空间中不同视口输出图形的显示方式, 选取对单个圆的凹多边形裁剪和对百万级数量的直线、圆的凹多边形裁剪.
(1) 系统仿真实验环境
系统仿真实验环境为3.2 GHz CPU, 4 GB内存, 1 TB硬盘, 64位的Windows 7操作系统. 实验由一个可执行程序, 通过读取XML文件生成裁剪边界和被裁剪的图形, 并且统计有多少个图形与边界相交(交点数), 有多少个图形在边界内部, 有多少个图形在边界外部.
(2) 单个圆裁剪
对单圆的凹多边形裁剪的执行结果、算法执行效率和内存消耗如图4所示, 裁剪后圆在多边形边界外的部分不显示, 在多边形边界内的部分正确显示, 单一数据验证算法的正确性.

|
图 4 对一个单圆的裁剪 |
(3) 百万级数量的线段和圆裁剪
为测试算法的通用性, 选取不同随机斜率下的线段和区域内不同随机原点不等半径下的圆进行凹多边形裁剪. 对百万级数量的线段和圆进行裁剪, 以进一步验证裁剪算法的正确性. 裁剪前图形显示如图5所示, 蓝色表示区域内不同原点、不等半径下的圆, 绿色表示不同斜率下的线段.

|
图 5 裁剪前图形 |
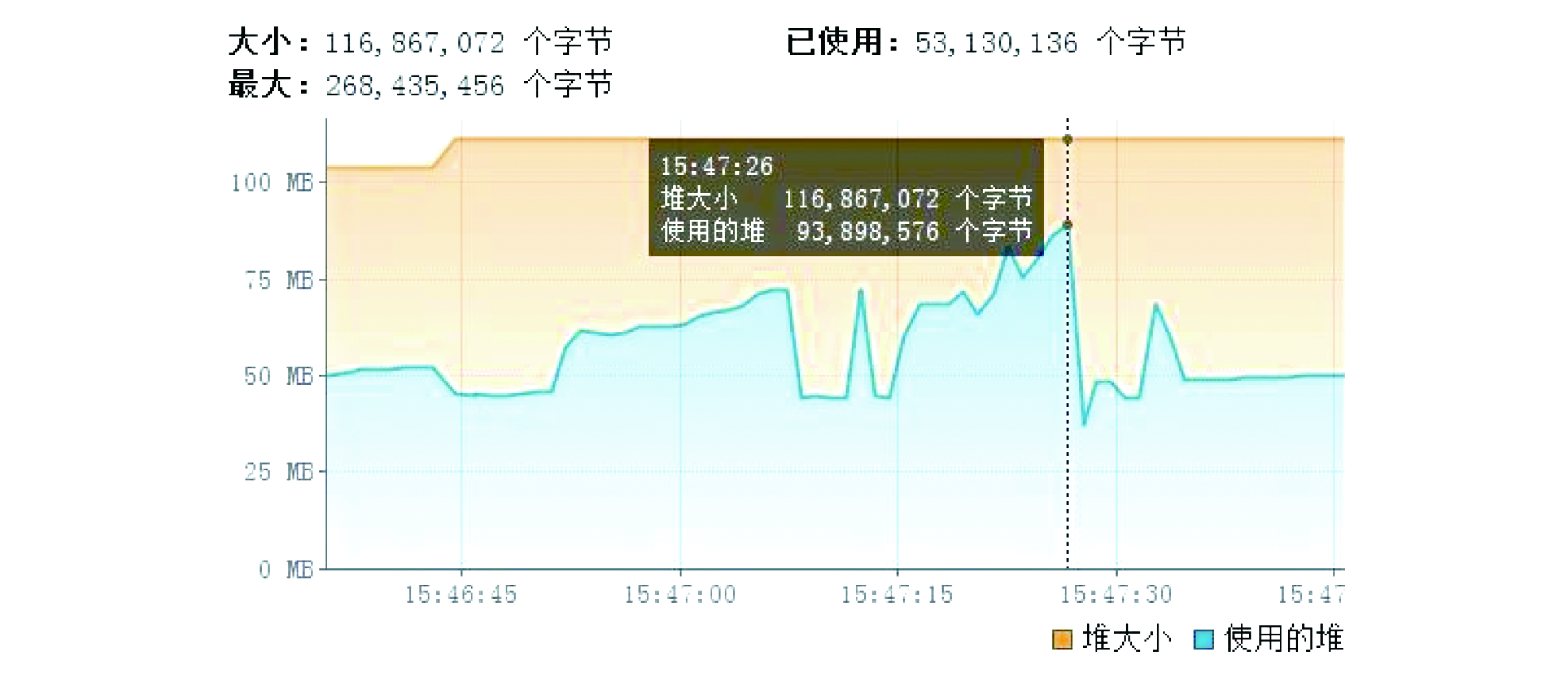
在执行裁剪操作后, 统计完成裁剪显示后时间和内存达到非功能性需求的结果. 使用传统裁剪算法的运行内存和时间消耗, 如图6、图7所示. 使用改进后裁剪算法的运行内存和时间消耗, 如图8、图9所示.
|
图 6 传统裁剪算法的执行内存消耗 |
|
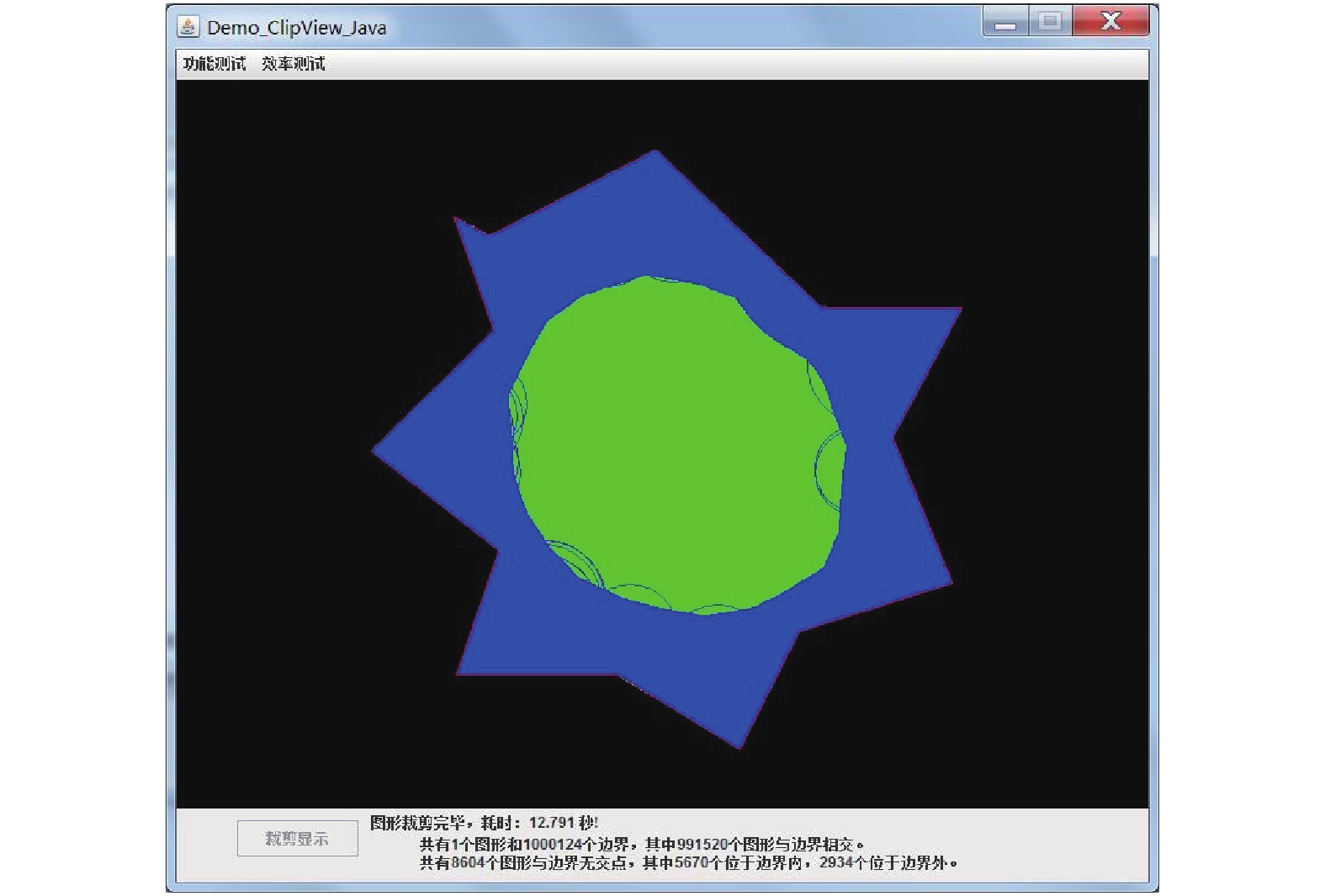
图 7 传统裁剪算法的执行时间消耗 |

|
图 8 改进后裁剪算法的执行内存消耗 |
|
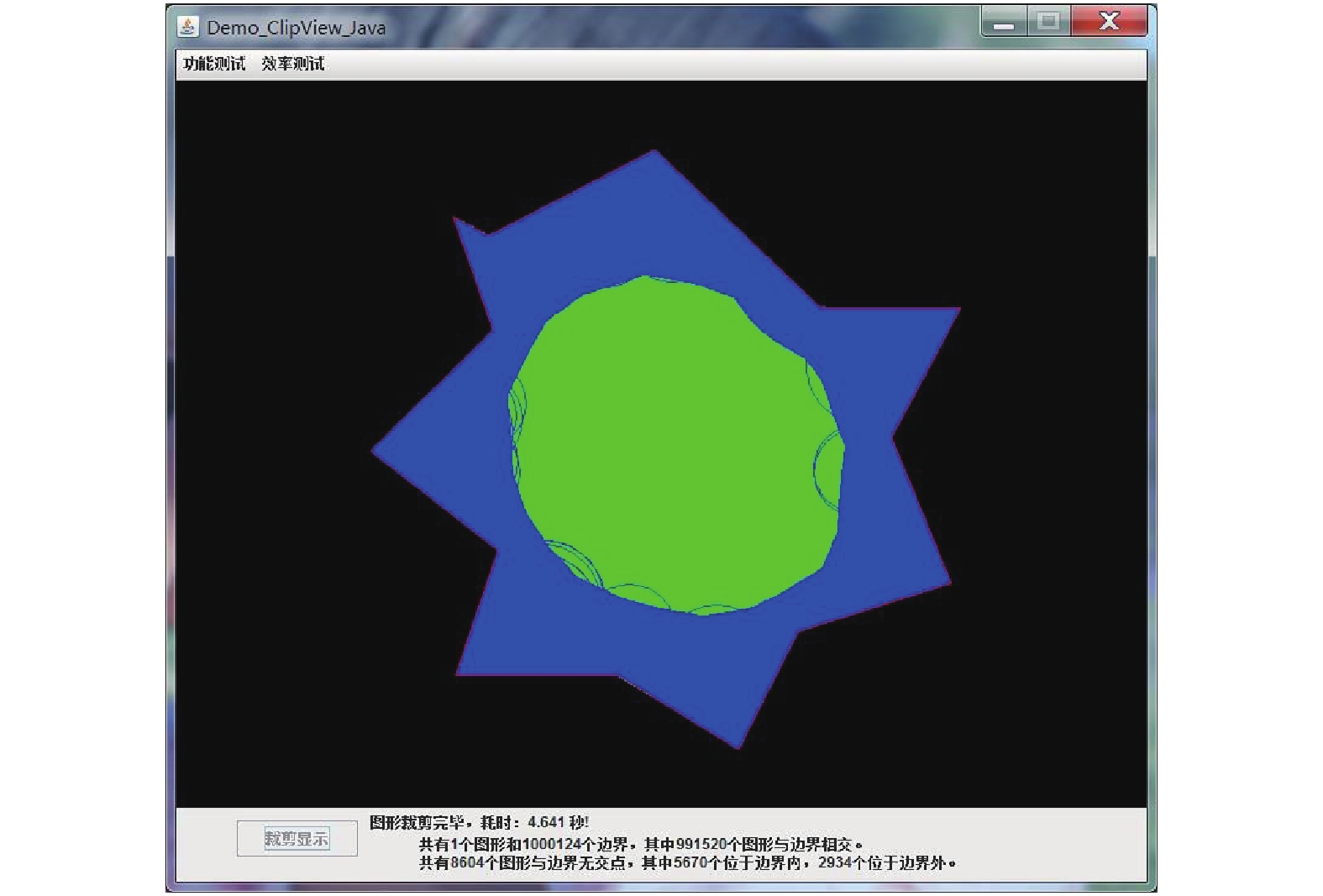
图 9 改进后裁剪算法的执行时间消耗 |
(4) 实验结果分析
实验对1000 124个图形进行裁剪, 有991 520个图形与边界相交(交点数), 有5670个图形在边界内部, 有2934个图形在边界外部. 裁剪后线段显示均在凹多边形内部, 裁剪后圆在裁剪边界外的部分不显示, 在裁剪边界内的部分正确显示.
实验结果显示传统裁剪算法的执行时间为12.791 s;运行过程中, 内存随计算机运行状态有所变化, 我们取内存中堆的使用峰值为93 898 576个字节. 采用改进后裁剪算法的执行时间为4.641 s, 远小于12.791 s, 在算法的执行时间上大大缩短了, 内存中堆的使用峰值为76 156 576个字节, 所占空间明显降低.
5 总结本文针对传统计算机图形学中的矢量图形裁剪算法进行改进, 通过实时高效地计算矢量图形(line、circle)与非矩形的且非自交的多边形的交点, 通过对交点的排序与分析, 判断图形与多边形边界的内、外部关系, 从而决定其裁剪后的图形显示结果. 改进算法主要围绕降低循环中冗余计算、重用对象、多线程控制等方面进行改进. 改进后的算法在程序执行时间和内存消耗方面均优于传统的矢量图裁剪算法. 此算法的实现为提高工程图形的生成效率提供了一种新的方法. 但本算法只是模拟CAD软件的布局空间中不同视口输出图形的显示方式来仿真实验, 还需要进一步嵌入到具体的应用软件中来验证其算法的执行效率和内存消耗问题.
| [1] |
Chlebus E, Krot K. CAD 3D models decomposition in manufacturing processes. Archives of Civil and Mechanical Engineering, 2016, 16(1): 20-29. DOI:10.1016/j.acme.2015.09.008 |
| [2] |
Qin FW, Li LY, Gao SM, et al. A deep learning approach to the classification of 3D CAD models. Journal of Zhejiang University Science C, 2014, 15(2): 91-106. DOI:10.1631/jzus.C1300185 |
| [3] |
Koch S, Behrens BA, Hübner S, et al. 3D CAD modeling of deep drawing tools based on a new graphical language. Computer-Aided Design and Applications, 2018, 15(5): 619-630. DOI:10.1080/16864360.2018.1441228 |
| [4] |
Scheffler R, Murugan VR, Wrobel G, et al. Graphical modelling of a meta-model of CAD models for deep drawing tools. INCOSE International Symposium, 2016, 26(1): 1090-1104. DOI:10.1002/iis2.2016.26.issue-1 |
| [5] |
Elias R. 2D graphics. Elias R. Digital Media: A Problem-Solving Approach for Computer Graphics. Cham: Springer International Publishing, 2014. 9–64.
|
| [6] |
Jeli Z, Popokonstantinovic B, Stojicevic M. Usage of 3D computer modelling in learning engineering graphics. Cvetković D. Virtual Learning. London: IntechOpen, 2016.
|
| [7] |
苗永春, 唐权华. 任意多边形窗口的矢量圆裁剪算法. 计算机辅助设计与图形学学报, 2016, 28(9): 1451-1458. DOI:10.3969/j.issn.1003-9775.2016.09.007 |
| [8] |
Hua H. Irregular architectural layout synthesis with graphical inputs. Automation in Construction, 2016, 72: 388-396. DOI:10.1016/j.autcon.2016.09.009 |
| [9] |
汤德佑, 周子琳. 基于临界多边形的不规则件启发式排样算法. 计算机应用, 2016, 36(9): 2540-2544. |
| [10] |
Mirza MJ, Tahir MW, Anjum N. On singularities computation and classification of redundant robots. Proceedings of International Conference on Computing, Communication and Control Engineering. Dubai, UAE. 2015. 12–16.
|
| [11] |
Yüksek K, Alparslan M, Mendi E. Effective 3-D surface modeling for geographic information systems. Natural Hazards and Earth System Sciences, 2016, 16(1): 123-133. DOI:10.5194/nhess-16-123-2016 |
| [12] |
刘凯. AutoCAD坐标标注在工程图中的应用. 软件导刊, 2015, 14(1): 52-53. |
 2018, Vol. 27
2018, Vol. 27


