OFDM多载波调制系统是基于频分复用(Frequency Division Multiplexing, FDM)技术的通信系统. 其原理是通过对多路调制信号进行不同载频的调制, 使得多路信号的频谱在同一个传输信道的频率特性中互不重叠, 从而完成在一个信道中同时传输多路信号的目的^[1]. 目前, OFDM是使用最广泛的多载波调制技术, OFDM采用矩形窗作为原型滤波器和正交子载波的设计方案, 其调制方式正好与快速傅里叶算法(Fast Fourier Transform, FFT)相匹配^[2], 并且因为其简单易实现和高效的频谱利用率得到了普遍应用, 而且在理想情况中, 利用子载波的正交特性, 接收端系统可以完全无损的恢复出发射信号.

随着OFDM调制技术的不断发展和演进, 正交频分复用/偏移正交幅度调制(OFDM/Offset QAM, OFDM/OQAM)系统作为OFDM的一种改进的替代方案被提出, 其调制技术不需要插入保护间隔, 具有更高的频谱效率．采用良好的时频特性成形滤波器, 可以同时抵抗符号间干扰(ISI)和信道间干扰(ICI)^[3].

随着多载波调制技术的快速发展, 认知无线电(Cognitive Radio, CR)技术同样被认为是提高授权频段利用率最有前景的解决方案^[4]. 调制识别是认知无线电中的重要技术, 在认知无线电, 广播活动的监视和控制, 电子战和频谱监测管理等各种军事和民用应用中起着至关重要的作用^[5].

文献[6]提出一种基于谱分析的OFDM调制识别方法, 这种方法具有在理想高斯信道下正确识别率高, 计算量较小等特点, 但对于子载波数较少的OFDM信号识别具有局限性. 文献[7]利用OFDM信号的循环累积量和自相关特性的方法实现了OFDM信号的调制识别, 在实际应用中, 峰度统计量采用样本的四阶矩, 所以鲁棒性很差, 在低信噪比情况下识别效率显着降低. 文献[8]通过一种基于循环自相关函数的方法解决了OFDM调制识别的问题. 基于星座图的信号调制识别方法在近几年中被广泛研究^[9–13]. 文献[9]提出接收信号星座图恢复方法并利用改进的减法聚类算法将调制信号的星座图根据方形星座图的对称性, 将星座图中的星座点投影到x轴或y轴上. 这种方法较大地提高了聚类点的密度指标, 改善了聚类分析的性能. 但其以聚类中心投影后的点数为标准对MQAM信号进行分类, 无法实现QPSK和BPSK的分类, 且在信号调制识别前需要使用匹配滤波器和抽样判决对接收信号进行星座图恢复, 其增加了系统硬件实现的复杂度. 随着各种新型调制方式的出现,仍有不少问题亟待解决^[14]. 尤其是OFDM-OQAM技术的提出使得这种信号的调制识别成为了一个需要解决的问题.

目前信号调制识别的方法一般有两类: 判决理论方法和模式识别方法. 判决理论方法主要是计算信号的似然函数, 得到用于分类的统计量, 然后设置一个合适的判决门限进行比较. 模式识别方法主要是提取信号的特征参数, 并将分类特征参数值输入分类器进行训练, 实现识别功能. 前者需要更多的先验条件且计算量大, 对参数偏差比较敏感, 后者则更依赖于分类器的建立. 本文将这两种方法结合, 利用模式识别方法提取的特征参数为判决理论方法提供先验条件, 使用后者的判决门限进行分类. 考虑到星座图是数字调制的一个重要特征, 能反映信号结构及不同调制状态的关系, 所示文中直接提取其星座图的特征参数再结合似然函数完成MPSK、MQAM和OQAM子载波调制信号的调制识别.

1 信号模型

OFDM调制系统中, 子载波的调制方式由系统需求所决定, 对于其子载波的调制识别也会存在一定难度. 在加性高斯白噪声信道中, 接收端OFDM信号模型如下:

$X\left( t \right) = \mathop \sum \limits_{k = 1}^N \left ({a_k}\cos{w_c}t + {b_k}\sin{w_c t} \right ) + {{n}}\left( t \right)$

(1)

子载波信号模型如下:

$\begin{aligned}r\left( t \right) = \sqrt {{p_t}} \left( {\mathop \sum \limits_{n = - \infty }^\infty {a_n}h\left( {t - nT} \right)} \right)\cos {w_c}t \\\;\;\;\; -\sqrt {{p_t}} \left( {\mathop \sum \limits_{n = - \infty }^\infty {b_n}h\left( {t - nT} \right)} \right)\sin{w_c}t\end{aligned}$

(2)

式(1)中, ${a_k} = \sqrt {{p_t}} \left( {\displaystyle\mathop \sum \limits_{n = - \infty }^\infty {a_n}h\left( {t - nT} \right)} \right)$ , ${b_k} =$ $ \sqrt {{p_t}} \left( {\displaystyle\mathop \sum \limits_{n = - \infty }^\infty {b_n}h\left( {t - nT} \right)} \right)$ . ${a_n},{b_n}$ 是独立均为分布的二元序列, T为符号时间, h(t)为持续时间为T的单位功率脉冲波形. ${p_t}$ 为带信号功率, n(t)是单边功率谱密度为N₀的高斯白噪声.

2 基于星座图聚类投影与对数似然函数的算法 2.1 算法流程

本文采用模式识别与判决理论结合的方法, 解决了单一调制识别算法存在的计算量大、对参数偏差敏感等问题, 具体算法如下.

(1) 对子载波调制信号的星座图进行聚类投影, 并利用聚类投影结果的最大距离点与最小距离点的比值最为特征参数, 对MPSK和MQAM调制类型进行粗分类.

(2) 根据调制类型的不同, 得到MPSK和MQAM的条件概率 ${{p}}\left( {\theta |{m_i}} \right)$ , 求得MPSK和MQAM子载波接收信号的条件似然函数 ${{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right)$ 和OQAM的条件似然函数 ${{p}}\left( {{{{X}}_k}\left( n \right){\rm{|\theta }}} \right)$ .

(3) 由子载波接收信号的 ${{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right)$ 推导出多个子载波接收信号的条件似然函数 ${{p}}\left( {{{X}}\left( n \right)|{m_i}} \right)$ 降低误分类概率, 并求其对数似然函数.

(4) 根据多个子载波调制方式的 ${{LL}}{{{F}}_X}$ 计算值来设置检测门限并分类不同子载波调制方式.

2.2 基于星座图聚类算法的子载波调制识别

星座图可以比较直观地表现出调制信号的相位与幅度特征, 如图1所示.

从图1(a)可看出MPSK信号的各个星座点都在一个圆上, 且不同星座点的相位不同, 而图1(b)则可看出MQAM信号各个点的星座图分布在复平面的一定范围内, 如果相位相同则幅度必不相同, 如果幅度相同则相位必不相同.

本文对原有星座图调制识别方法进行改进, 提出一种新方法, 不需要对接收信号进行星座图恢复. 将接收信号的星座图点都投影在一、三象限的角平分线上, 在进行识别时只取第一象限的聚类中心点, 并求离原点最远和最近点的距离比值. 这样既使得聚类点的密度指标较高, 也避免了因为干扰较强导致的投影点数模糊. 将距离原点最远的聚类中心点的距离记为d_max, 将距离原点最近的聚类中心点的距离记为d_min, 并取D=d_max/d_min. 经过理论计算, 我们可以得到D的值, 如表1所示.

这种D值分类算法适合于所有的MQAM调制信号和部分MPSK信号, 因为BPSK和QPSK调制信号理论上在第一象限都只有一个聚类点(QPSK在原点处有一个点而BPSK没有), 所以这两种调制信号的D值无法计算, 但是可以直接利用d_max值对BPSK和QPSK分类而不需要计算D值.

文中所用聚类方法为减法聚类, 设{x₁, x₂, x₃, …,x_n}是n维空间中的聚类特征集, 将特征集内所有特征点都归一化到一个超立方体内. 定义特征点处的密度指标为:

${D_{{i}}} = \sum\limits_{j = {\rm{1}}}^n {\exp \left( - \frac{{{{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{{{\left(\displaystyle\frac{{{r_a}}}{2}\right)}^2}}}\right)} $

(3)

半径r_a是一个正数, 其定义了x_i的一个邻域, 半径以外的特征点对x_i的密度指标影响很小. 在计算完所有特征点的密度指标后, 选择其中具有最高密度指标的特征点作为第一个聚类中心点x_c1, 其密度指标为D_c1. 接着对每个聚类特征点的密度指标进行修正, 修正半径为r_b, 修正公式为:

${D_{{i}}} = {D_{{i}}} - {D_{c1}}\exp \left( - \frac{{{{\left\| {{x_i} - {x_{c1}}} \right\|}^2}}}{{{{\left(\displaystyle\frac{{{r_b}}}{2}\right)}^2}}}\right)$

(4)

2.3 基于对数似然函数的多载波信号调制识别

但上一步算法虽然利用星座图聚类投影方法能对MPSK和MQAM信号分类识别, 却无法对OFDM解调后得到的OQAM信号进行分类, 因为OQAM调制在QAM调制的基础上还进行了预处理使得实部和虚部错开1/2个周期, 所以必须经过对数似然函数算法再对上一步算法得到的结果进行进一步分类, 从而识别出OQAM信号.

X_k(n)表示第k个子载波的接收信号, 使用 ${m_i}$ ( $i$ =2, 4, 8, 16,…)表示识别出的子载波调制类型, 则:

${{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right) = {{p}}\left( {{{{X}}_k}\left( n \right){\rm{|\theta }}} \right) \times {{p}}\left( {{\rm{\theta }}|{m_i}} \right)$

(5)

式(5)中, ${{p}}\left( {{{{X}}_k}\left( n \right){\rm{|\theta }}} \right)$ 为第k个子载波的接收信号的条件似然函数. ${{p}}\left( {{\rm{\theta }}|{m_i}} \right)$ 为已知信号调制方式下的载波相位的条件似然函数. ${{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right)$ 表示第k个子载波接收信号在已知调制方式下的条件似然函数, 即这个接收信号属于调制方式 ${m_i}$ 的概率. 但对于OQAM信号, 因为其没有从上一步算法中分类出来, 所以只需推导计算其 ${{p}}\left( {{{{X}}_k}\left( n \right){\rm{|\theta }}} \right)$ . 其中文献[15]指出, 对于子载波接收信号 ${{r}}\left( t \right)$ 的联合条件概率密度为:

$\begin{array}{l}{{P}}\left( {{{r}}\left( t \right)|{a_n},{b_n},h\left( t \right),{\theta _c}} \right) = \\\!\!\!\!{\rm{Cexp}}\left( { - {{N\gamma }}} \right)\exp\left[ {\displaystyle\frac{{2\sqrt {{p_t}} }}{{{N_0}}}\mathop \sum \limits_{n = 0}^{N - 1} {a_n}\mathop \smallint \limits_{nT}^{\left( {n + 1} \right)T} r\left( t \right)h\left( {t - nT} \right)\cos {w_c}tdt} \right]\\ \times \exp\left[ { - \displaystyle\frac{{2\sqrt {{p_t}} }}{{{N_0}}}\mathop \sum \limits_{n = 0}^{N - 1} {b_n}\mathop \smallint \limits_{nT}^{\left( {n + 1} \right)T} r\left( t \right)h\left( {t - nT} \right)\sin {w_c}tdt} \right]\end{array}$

(6)

式(6)中 ${p_t}$ 为信号功率, 使用 ${\rm{\gamma }} \triangleq \displaystyle\frac{{{p_t}T}}{{{N_0}}}$ 表示信噪比. $h\left( t \right)$ 为成形脉冲. T为符号时间. C为常数, N为符号个数. ${a_n}$ 、 ${b_n}$ 为独立均匀分布的二元( $ \pm 1$ )序列. ${N_0}$ 为加性高斯白噪声的单边功率谱密度. 将式(6)转换到复基带上, 定义I路和Q路复数基带匹配滤波器输出为:

$\left\{ \begin{array}{l}{{\tilde r}_{{\rm{I}}n}} = \displaystyle\frac{1}{T}\int_{nT}^{(n + 1)T} {\tilde r(t)p(t - nT)} dt\\{{\tilde r}_{{\rm{Q}}n}} = \displaystyle\frac{1}{T}\int_{nT}^{(n + 1)T} {\tilde r(t)p[t - nT]} dt\end{array} \right.$

(7)

将式(7)代入式(6)并使用 ${\sigma ^2} = {N_0}/T$ 化简上式后再分别在I、Q路数据和 ${a_n}$ 、 ${b_n}$ 上进行平均^[15], 所以可得出:

$\begin{array}{l}\!\!\!\!\!{{P}}\left( {{{r}}\left( t \right){\rm{|}}{\theta _c}} \right) = {\rm{Cexp}}\left( { - {{N\gamma }}} \right) \times \exp\displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \ln \cosh\left[ {\displaystyle\frac{{\sqrt {{p_t}} }}{{{\sigma ^2}}}{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {\rm{j}}{\theta _c}}}} \right)} \right]\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times \exp\displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \ln \cosh\left[ {\displaystyle\frac{{\sqrt {{p_t}} }}{{{\sigma ^2}}}{\rm{Im}}\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}{\theta _c}}}} \right)} \right]\\ = {\rm{Cexp}}\left\{ { - {{N\gamma }} + \displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \left[ {\ln \cosh{{\rm{x}}_{{\rm{I}}n}}\left( {{\theta _c}} \right) + \ln \cosh{{\rm{x}}_{{\rm{Q}}n}}\left( {{\theta _c}} \right)} \right]} \right\}\end{array}$

(8)

式(8)中:

$\left\{ {\begin{array}{*{20}{c}} {{{\rm{x}}_{{\rm{I}}n}}\left( {{\theta _c}} \right) \triangleq \displaystyle\frac{{\sqrt {{p_t}} }}{{{\sigma ^2}}}{\rm {Re}}\left( {{{\rm{r}}_{{\rm{I}}n}}{e^{ - {\rm{j}}{\theta _c}}}} \right)} \\ {{{\rm{x}}_{{\rm{Q}}n}}\left( {{\theta _c}} \right) \triangleq \displaystyle\frac{{\sqrt {{p_t}} }}{{{\sigma ^2}}}{\rm {Im}}\left( {{{\rm{r}}_{{\rm{Q}}n}}{e^{ - {\rm{j}}{\theta _c}}}} \right)} \end{array}} \right.$

(9)

存在三角恒等式:

${\rm{ln}}\left\{ {\frac{1}{2}\left[ {\cosh\left( {X + Y} \right) + \cosh\left( {X - Y} \right)} \right]} \right\} = \ln \cosh X + \ln \cosh Y$

(10)

利用式(10)中的三角恒等式使式(8)可变为:

$\begin{array}{l}\!\!\!\!\!P\left( {r( t )|{\theta _c}} \right) = C\exp \{ { - N\gamma } + \displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \ln \frac{1}{2} \left[ {\cosh ( {{x_{{\rm I}n}}( {{\theta _c}}) }} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+{x_{{\rm Q}n}}\left( {{\theta _c}} \right)\left. {\left. { + \cosh \left( {{x_{{\rm I}n}}\left( {{\theta _c}} \right) - {x_{{\rm Q}n}}\left( {{\theta _c}} \right)} \right)} \right]} \right\}\end{array}$

(11)

因为取对数可以适应似然函数的大动态变化, 而 $C\exp\left( { - N\gamma } \right)$ 取对数后对结果影响很小,所以为了简化计算而将其忽略并使用近似关系:

$\left\{ {\begin{array}{*{20}{c}} {{\rm{cosh}}x \approx 1 + \displaystyle\frac{{{x^2}}}{2}} \\ {\ln \left( {1 + {\rm{x}}} \right) \approx x} \end{array}} \right.$

(12)

将式(11)可变为:

$\begin{array}{l}P\left( {{{r}}\left( t \right){\rm{|}}{\theta _c}} \right) = \exp\left\{ {\displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \displaystyle\frac{{{p_t}}}{{2{\sigma ^4}}}} \right.\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {{j}}{\theta _{{c}}}}}} \right)} \right)}^2}} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. { + {\rm{Im}}{{\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}{\theta _{{c}}}}}} \right)}^2}} \right]} \right\}\end{array}$

(13)

在MPSK调制中, 共有M种相位, 而在常见的QAM调制中, 16QAM有12种相位, 32QAM有28种相位, 64QAM有44种相位. OQAM信号没有星座图, 所以在下一步推理计算中不需要带入 ${{p}}\left( {{\rm{\theta }}|{m_i}} \right)$ . 因而对于MPSK调制信号和常见的QAM调制信号, 其相位属于调制方式 ${m_i}$ 的概率如下:

$\left\{ {\begin{aligned}&{p\left( {{\rm{\theta }}|{m_i}} \right) = \displaystyle\frac{1}{M}\;\;\;\;{\rm {MPSK}}{\text{调制信号}}}\\&{p\left( {{\rm{\theta }}|{m_i}} \right) = \displaystyle\frac{1}{{12}}\;\;\;\;{\rm {16QAM}}{\text{调制信号}}}\\&{p\left( {{\rm{\theta }}|{m_i}} \right) = \displaystyle\frac{1}{{28}}\;\;\;\;{\rm {32QAM}}{\text{调制信号}}}\\&{p\left( {{\rm{\theta }}|{m_i}} \right) = \displaystyle\frac{1}{{44}}\;\;\;\;{\rm {64QAM}}{\text{调制信号}}}\end{aligned}} \right.$

(14)

令 ${\rm{\alpha }} \triangleq {\rm{p}}\left( {{\rm{\theta }}|{m_i}} \right)$ , 则:

$\begin{aligned}&{{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right) = {{p}}\left( {{{{X}}_k}\left( n \right){\rm{|\theta }}} \right) \times {{p}}\left( {{\rm{\theta }}|{m_i}} \right)\\& = {{p}}\left( {{{r}}\left( t \right){\rm{|}}{\theta _c}} \right) \times \alpha \\& = \alpha \exp\left\{ {\displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \displaystyle\frac{{{p_t}}}{{2{\sigma ^4}}}\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {{j}}{\theta _c}}}} \right)} \right)}^2}{\rm{ + Im}}{{\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}{\theta _c}}}} \right)}^2}} \right]} \right\}\end{aligned}$

(15)

上式就表示第k个子载波接收信号在已知调制方式下的条件似然函数. 对式(15)取对数得到对数似然函数:

$LL{F_{{X_k}}} = {\rm{ln}}\left( {\rm{\alpha }} \right)\mathop \sum \limits_{n = 0}^{N - 1} \frac{{{p_t}}}{{2{\sigma ^4}}}\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {{j}}{\theta _c}}}} \right)} \right)}^2} + {\rm{Im}}{{\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}{\theta _c}}}} \right)}^2}} \right]$

(16)

在多载波调制中, 子载波调制方式一般是相同的. 虽然OFDM中可能会根据各个子载波处信道特性的优劣不同采用不同的调制方式, 但在子信道中的调制方式是相同的, 并且子载波之间采用正交等方法消除子载波间干扰, 所以子载波之间往往都是相互独立的^[16]. 因为在OFDM系统中, 子载波组中的调制信号通常使用相同的调制方式, 因此当k增加时, 可以降低误分类概率^[17], 所以其子载波组的条件似然函数如下式:

$\begin{aligned}{{p}}\left( {{{X}}\left( {{n}} \right)|{m_i}} \right) &= \mathop \prod \limits_{k = 1}^K {{p}}\left( {{{{X}}_k}\left( n \right)|{m_i}} \right) = \mathop \prod \limits_{k = 1}^K {\rm{\alpha exp}}\left\{ {\displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \displaystyle\frac{{{p_t}}}{{2{\sigma ^4}}}\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {{j}}{\theta _c}}}} \right)} \right)}^2} + {\rm{Im}}{{\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}{\theta _{{c}}}}}} \right)}^2}} \right]} \right\}\\& = {\alpha ^K}\exp\left\{ {\displaystyle\mathop \sum \limits_{k = 0}^K \displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \displaystyle\frac{{{p_t}}}{{2{\sigma ^4}}}\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {{j}}2{\rm{\pi }}{f_k}t}}} \right)} \right)}^2} + {\rm{Im}}{{\left( {{{{r}}_{{\rm{Q}}n}}{e^{ - {{j}}2{\rm{\pi }}{f_k}t}}} \right)}^2}} \right]} \right\}\end{aligned}$

(17)

式(17)中, ${f_k} = k/{{T}}$ , 为第k个子载波上的载波频率. 对式(17)取对数得到对数似然函数:

$\begin{aligned}{{LL}}{{{F}}_X} = &{\rm{ln}}\left( {{\alpha ^K}} \right)\displaystyle\mathop \sum \limits_{k = 0}^K \displaystyle\mathop \sum \limits_{n = 0}^{N - 1} \displaystyle\frac{{{p_t}}}{{2{\sigma ^4}}}\left[ {{{\left( {{\rm{Re}}\left( {{{{r}}_{{\rm{I}}n}}{e^{ - {\rm{j}}2{\rm{\pi }}{f_k}t}}} \right)} \right)}^2}} \right.\\&\left. { + {\rm{Im}}{{\left( {{{\rm{r}}_{{\rm{Q}}n}}{e^{ - {{j}}2{\rm{\pi }}{f_k}t}}} \right)}^2}} \right]\end{aligned}$

(18)

最后, 分别求得子载波信号的对数似然函数 ${{LL}}$ ${{{F}}_{{X_k}}}$ 和子载波组的对数似然函数 ${{LL}}{{{F}}_X}$ 并对其结果取绝对值, 并求其在不同调制方式的中值作为判决门限.

3 仿真结果与分析

本次实验仿真采用YunSDR-Y310软件无线电平台, 这个平台能实现频谱范围70 MHz~6 GHz、模拟带宽200 KHz~56 MHz的宽频段软件无线电系统. 此平台开发环境是Matlab, 使用Matlab工具配置频带参数并发送产生的信号数据, 通过Matlab获取射频前端采集到的信号数据.

仿真参数为: OFDM符号周期为3.2 μs, 信噪比为15 dB, 子载波间隔为312.5 KHz, 子载波数为100, 符号数为100, 信道传输衰减为20e3 dB. BPSK、QPSK、8PSK、16QAM, 32QAM和64QAM信号的聚类半径分别取0.5、0.3、0.2、0.21、0.112和0.098, 可以得到较好的聚类结果.

3.1 基于星座图的聚类算法的调制识别

常见的子载波调制信号BPSK, QPSK, 8PSK, 16QAM, 32QAM, 64QAM的星座图聚类并投影的结果如图2所示.

从图2(a)和图2(b)可以看出BPSK和QPSK的投影结果的区别, 因为这两个信号的投影结果受噪声影响较小所以可以直接从投影结果中分类. 所以8PSK、16QAM、32QAM和64QAM接收信号的D参数值如表2所示.

由表2可见, 这几种接收信号的D参数值与理论计算的数值非常接近, 故这种方法在调制阶数较高的情况下能解决传统聚类分类算法由于结果模糊而无法得出结论的问题, 能更好地对高阶MPSK和MQAM信号进行识别与分类.

3.2 基于对数似然函数的多载波信号识别仿真

经过Matlab仿真计算, 子载波为BPSK、QPSK、8PSK、16QAM、32QAM、64QAM和OQAM(调制阶数为16)调制方式的的 ${{LL}}{{{F}}_{{{{X}}_k}}}$ 与 ${{LL}}{{{F}}_{{X}}}$ 的值比较结果如表3所示.

由表3可得出, 在多载波调制系统内, 不同子载波调制方式的 ${{LL}}{{{F}}_{{{{X}}_{{k}}}}}$ 值不同但差异较小, 容易产生误分类, 而不同子载波的 ${{LL}}{{{F}}_{{X}}}$ 值差别很大, 很容易根据各子载波调制方式的 ${{LL}}{{{F}}_{{X}}}$ 函数结果的中值设置门限, 将具有不同子载波调制方式的多载波信号进行分类.

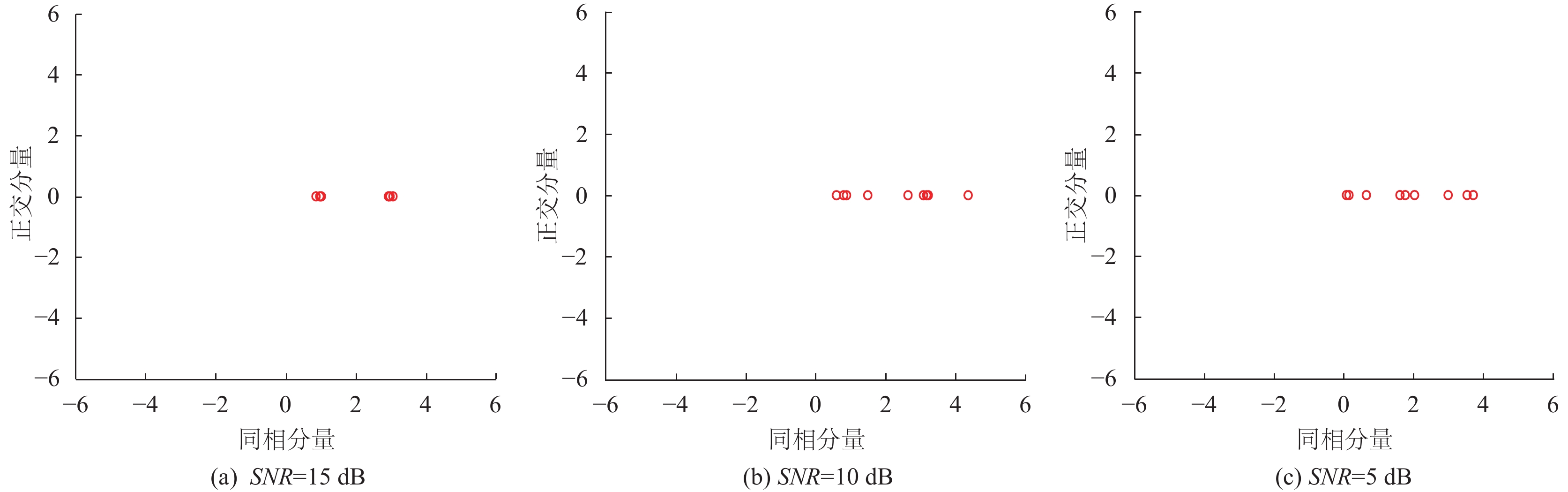
由于OFDM多载波调制系统的实现较为复杂, 为了降低其复杂度, 实验中没有对接收信号进行星座图恢复. 从图3和图4可以看出在不经过星座图恢复的情况下, 文献[9]中通过聚类中心点数进行调制识别的方法已无法在SNR<15 dB的情况下有效识别出8PSK和16QAM信号. 且基于星座图的方法对于没有经过后处理的OQAM信号根本无法识别. 而本文提出的方法在使用星座图调制识别的基础上结合了判决理论法, 能够达到较好的识别效果. 对实验所用每种信号均进行100次独立的随机仿真实验后, 其识别率如表4所示.

表4给出了本文提出方法对于不同子载波的识别率, 可看出当SNR<10 dB时识别率存在较大程度的降低, 这是由于接收端没有进行星座图恢复而直接使用噪声较大的接收信号进行调制识别而造成. 而同样情况下, 文献[9]的方法已无法对接收信号进行识别.

因此本文提出的方法在没有对接收信号进行消噪、星座图恢复情况下降低了硬件复杂度, 提升了信号的识别率.

4 结论与展望

通过理论研究提出了一种新的基于星座图聚类投影与对数似然函数的多载波系统中信号调制识别的方法. 这种方法改进了以往星座图聚类识别算法, 并结合了对数似然函数分类算法, 对不同子载波调制方式进行了分类, 最终通过实验仿真验证了理论分析并得到了具体的仿真数值. 但实验结果表明此方法在信噪比小于10 dB的情况下对于信号的调制识别效率较低, 这是因为接收端没有进行相关的去噪和信号恢复等工作, 虽然降低了硬件实现的复杂度, 但识别率降低了. 所以接下来的工作将对一种高效且低硬件复杂度的方法进行研究, 以解决该方法出现的问题. 并在此基础上进一步使用本文中的算法对不同多载波信号进行调制识别.