蚁群算法是一种启发式全局优化算法, 车辆路线问题(VRP)是指一定数量的客户具有不同数量的货物需求, 配送中心向客户提供货物, 由一个车队负责分送货物并组织适当的行车路线, 最终达到诸如路程最短等目的优化问题, 其最早是由Dantzig和Ramser于1959年首次提出的[1]. 早在1999年, Dorigo[2]和Gambardella[3]等学者首次将蚁群算法用来求解VRP问题, 此后大量国内外学者在蚁群算法在车辆路径问题方面的应用开展了研究工作. 如文献[4]把蚁群算法和遗传算法进行结合; 文献[5]将粒子群和蚁群算法进行结合; 文献[6]把车辆容量引入状态转移规则的更新公式中; 文献[7]通过定义蚂蚁权重来更新信息素; 文献[8]用改进后的蚁群算法对各类车辆路径问题进行求解并对比实验结果; 文献[9]采用了混合局部搜索算子, 增强了算法的局部寻优能力; 文献[10]对应用蚁群算法解决VRP问题做了整体回顾.
Petri网是1962年德国学者Petri[11]在其博士论文中提出的. Petri网是一个图形化数学化的模型工具, 适用于描述并发、异步、分布式、并行、非确定性或随机的信息处理系统, 应用于各种领域[12–15].
本文一方面对传统的蚁群算法进行了改进, 把客户需求量, 车辆实时货物装载量加入可行解的构造过程, 在一定程度上优化了初始解; 实时记录目前的最优路径, 通过对比自动调整信息素的更新方式, 在替换最优路径的同时, 对当前路径进行惩罚或奖励; 同时对概率选择公式进行了改进, 避免出现极端情况. 另外, 本文借助CPN Tools仿真工具建立了改进蚁群算法的颜色Petri网模型, 最后对车辆路径问题的经典算例进行了实验仿真. 借助CPN这一工具, 不仅对蚂蚁选择路径以及信息素更新的整个过程一目了然, 在获得最短路径的同时又可以获取多条路径, 从而可以根据交通等情况进行不同的选择. 而且该模型的可扩展性高, 不仅适用于普通VRP问题, 对于不确定需求, 时间窗等复杂VRP只需调整元组的参数即可.
2 求解VRP的改进蚁群算法 2.1 可行解构造的改进在使用蚁群算法求解VRP问题时, 蚂蚁是从所有未被服务的客户中按轮盘赌的方式进行选择, 而改进蚁群算法把客户需求和当前车辆的货物剩余量都考虑进去, 从而进一步缩小选择范围.
Step1. 从蚂蚁集合队列
约束条件1: 初始时access={所有等待服务的客户}, 遍历所有等待服务的客户, 如果该客户已被服务过, 从access列表中移除该客户; 更新access列表.
约束条件2: 遍历更新后的access列表中所有的客户, 考察客户的需求量是否满足蚂蚁
Step2. 从满足约束条件1和2的access列表中, 按照轮盘赌的方式, 随机选择一个客户进行服务.
Step3. 更新蚂蚁
Step4. 判断access是否为空, 如果为空, 说明蚂蚁
传统的ACO算法更新所有的可行解, 并按一定的比例挥发信息素. 本文信息素的变化分为增加和减少两类, 增加或减少的依据是当前可行解的路径长度
| $Tota{l_m} = \left\{ \begin{array}{l}Tota{l_d},\;Tota{l_d} < Tota{l_m}\\Tota{l_m},\;{\rm {otherwise}}\end{array} \right.$ | (1) |
该可行解路径上的所有客户的信息素τ按照公式(2)进行更新.
| ${\tau _{\rm {new}}}{\rm{ = }}\left\{ \begin{array}{l}{\tau _{\rm {now}}} + \displaystyle\frac{1}{{Tota{l_d}}},\;{\rm {if}}\;Tota{l_d} \le Tota{l_m}\\{\tau _{\rm {now}}} - \displaystyle\frac{1}{{Tota{l_d}}},\;\;{\rm {if}}\;\;Tota{l_d} > Tota{l_m} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm {and}}\;\;\left({\tau _{\rm {now}}} - \displaystyle\frac{1}{{Tota{l_d}}}\right) \ge 0\\0,\;{\rm {if}}\;\;Tota{l_d} > Tota{l_m}\;\;and\left( {{\tau _{\rm {now}}} - \displaystyle\frac{1}{{Tota{l_d}}}} \right) < 0\end{array} \right.$ | (2) |
如果路径不包括所有的客户, 那么蚂蚁是需要从其未访问的客户列表中随机选择一个客户进行服务的, 其选择客户的依据就是选择概率的大小. 因此概率公式的计算直接决定改可行解的质量. 因此, 既要考虑两客户之间的信息素的大小, 也需要考虑两者之间的距离, 并且还需要平衡两个因素的相对重要程度. 在
| ${p_i}_j = \left\{ \begin{array}{l}\displaystyle\frac{{{\tau _{ij}}^\alpha }}{{{d_{ij}}}}\;\;\;\;\;j \in Access\;\;\;{\rm {and}}\;\;{\tau _{ij}} \ne 0\\\displaystyle\frac{1}{{{d_{ij}}}}\;\;\;\;\;j \in Access\;\;\;{\rm {and}}\;\;{\tau _{ij}} = 0\;\end{array} \right.$ | (3) |
计算完蚂蚁当前所处的客户与未访问客户列表中任意两者之间的概率后, 为避免陷入局部最优, 采用轮盘赌的方式进行选择, 从而确定蚂蚁下一步要选择的服务客户.
3 改进蚁群算法的颜色Petri网模型 3.1 CPN模型及颜色集描述本文使用颜色Petri网工具CPN Tools[16]完成相应的建模, 该工具使用 Standard Programming Language(SML)语言完成相应的功能. 并且可以设置断点进行调试, ACO运行的每一个中间结果都可以通过软件实时观察到.
顶层(Top)CPN模型如图1所示, 展示了整个算法的流程. 三个替代变迁分别对应着三个具体的子页page. 替代变迁GetAnt完成对循环迭代次数的控制功能; 替代变迁AntChoiceCity生成可行解, 替代变迁UpdatePheromone更新信息素的更新.
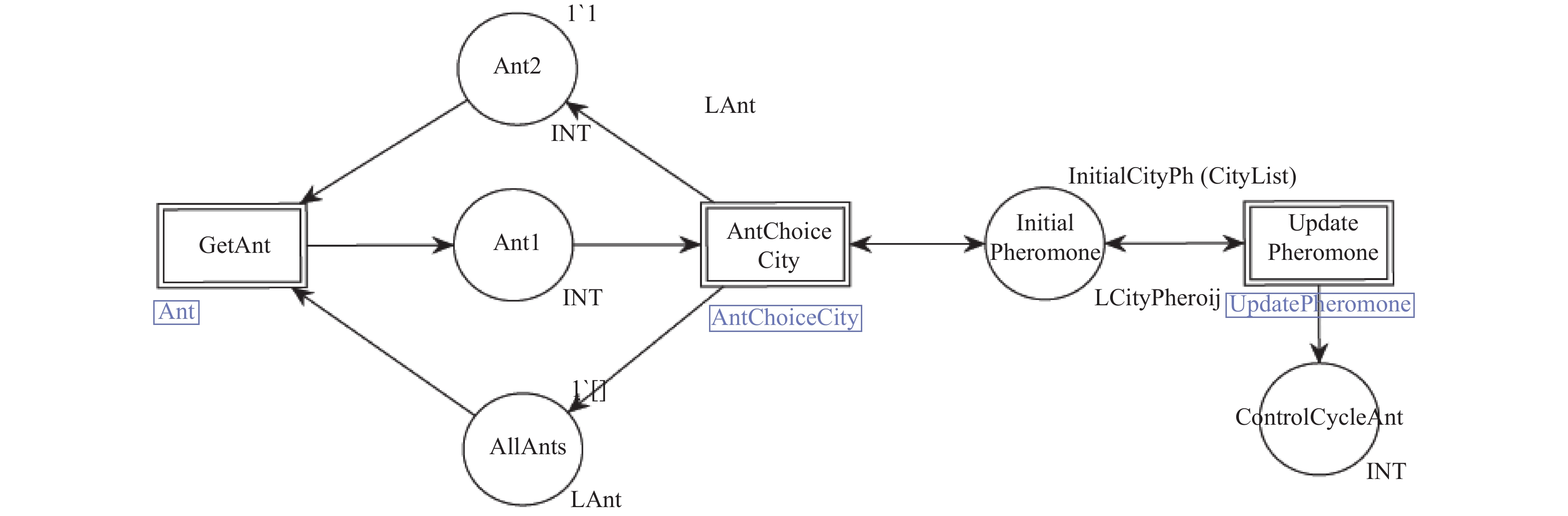
|
图 1 改进的ACO的CPN模型的top页 |
3.2 部分模型及主要函数
图2对应着可行解的生成过程, 蚂蚁从未服务的客户中进行初步选择, 然后再根据车辆目前的装载剩余量和未服务的客户列表中客户的需求量, 进一步对禁忌表进行更新, 最终形成符合两个条件的所有的客户列表. 然后再根据信息素和转移概率, 利用轮盘赌进行选择. 重复该过程, 直至不存在未被服务的客户. 该可行解进入下一步计算路径处理过程的同时开始进行下一轮可行解的构造过程.
其中库所AccessCity表示蚂蚁下一步可选择的所有客户列表以及目前蚂蚁已经服务过的客户列表, 它的颜色集LAntCity是一个如下所示的五元组:
colset AntCity = product AntN*CurrentCity*PassCity
*LCityNum*REAL;
colset LAntCity = list AntCity;
其分别表示蚂蚁号、目前所在的客户编号、服务过的客户列表、下一步可选的客户列表以及目前车辆货物剩余量. 该库所是AccessCity变迁的输出, 存放输入变迁的结果, 同时为GenerateCityProbility这个变迁提供输入.
变迁AccessCity将产生蚂蚁可选择的客户列表, 其输入是已经服务过的客户列表, 输出下一步可以选择的客户列表. 这个功能是由函数AntCityAccessNew实现的. 而AccessCitybyDemandLast函数实现的是根据新的禁忌表和车辆的剩余装载量以及AntCityAccessNew函数的输出, 进一步按客户需求量更新禁忌表.
变迁GenerateCityProbility根据库所AccessCity中的令牌值, 所有客户之间的信息素, 以及列表中客户的选择概率, 通过轮盘赌的方法去选择一个客户, 并把选择的客户作为变迁UpdateAntPassCity的输入, 同时该变迁更新蚂蚁已经访问过的客户列表; 更新蚂蚁的新位置; UpdateAccessCus变迁负责更新禁忌表, 同时判断该蚂蚁目前的客户列表是否组成一个可行解, 是的话, 输出可行解的客户列表为计算可行解的路径长度提供输入, 同时, 更新蚂蚁列表; 如果还未形成可行解, 那么为蚂蚁新位置的下一次选择做准备.
4 测试实例为检验改进蚁群算法在求解车辆路径问题上的有效性, 实验采用国际公认的VRP问题库中的经典实例和其他参考文献中使用的实例作为实验对象.
1) 案例1[17]: 某配送中心用2辆额定装载量为8×103 kg的汽车对8个客户配送货物, 配送中心与客户、客户与客户之间的距离以及客户的需求量如表1所示, 其中, 0代表配送中心, 其他代表8个客户点. 其余参数的设置详见参考文献[17].
表2展示了本文算法与GA算法, 传统蚁群算法以及其他改进蚁群算法之间的对比, 本文算法在求得比GA算法和传统蚁群算法小的路径同时获得了三条最短路径. 所有可行解的分布情况如图3所示.
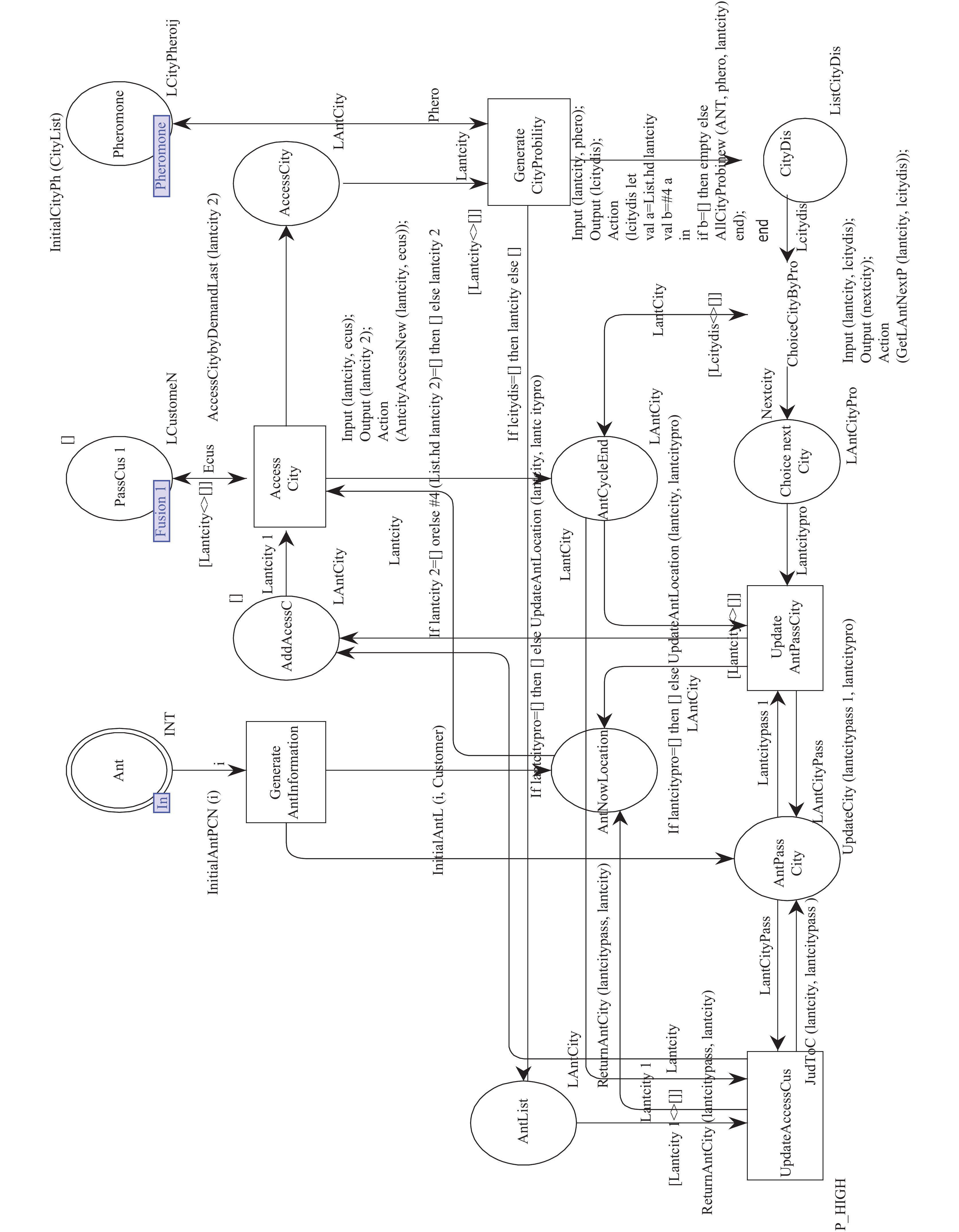
|
图 2 可行解生成过程 |
| 表 1 案例1的距离与需求量表 |
| 表 2 各算法之间的最优路径, 最优路径长度的对比 |
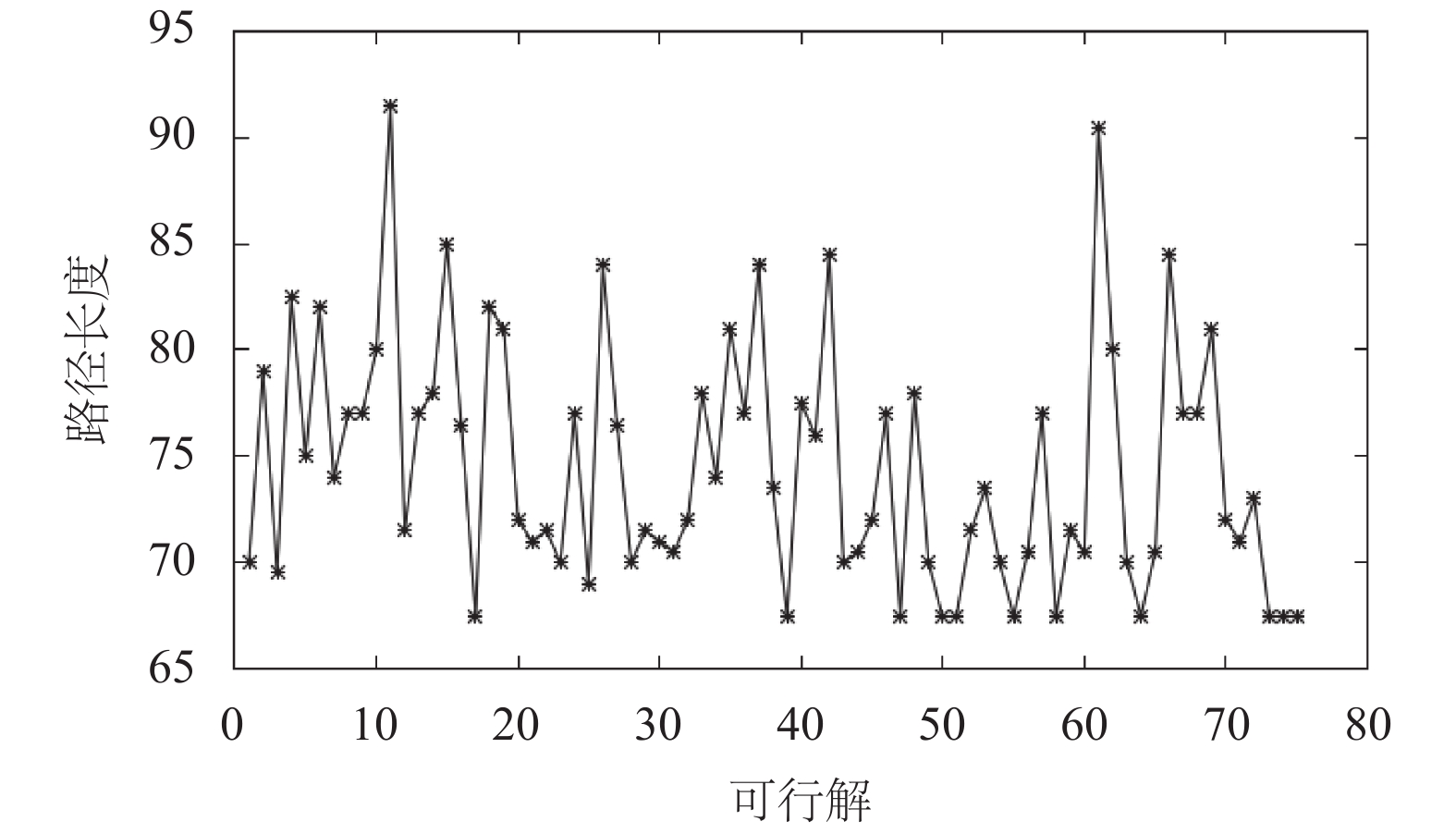
|
图 3 案例1所有可行解的分布情况图 |
2) 案例2(E016-03m): 某配送中心(编号为0)用3辆装载量为90吨的车辆对15个客户配送货物. 其余参数的设置详见参考文献[18]. 得到的最优解最优路径如图4所示.
图4(a)为本文算法, 最优路径长度为278.9, (b)为改进的遗传算法[19], 最优路径长度为285.7087, (c)为改进蚁群算法[18], 最优路径长度为284.105.
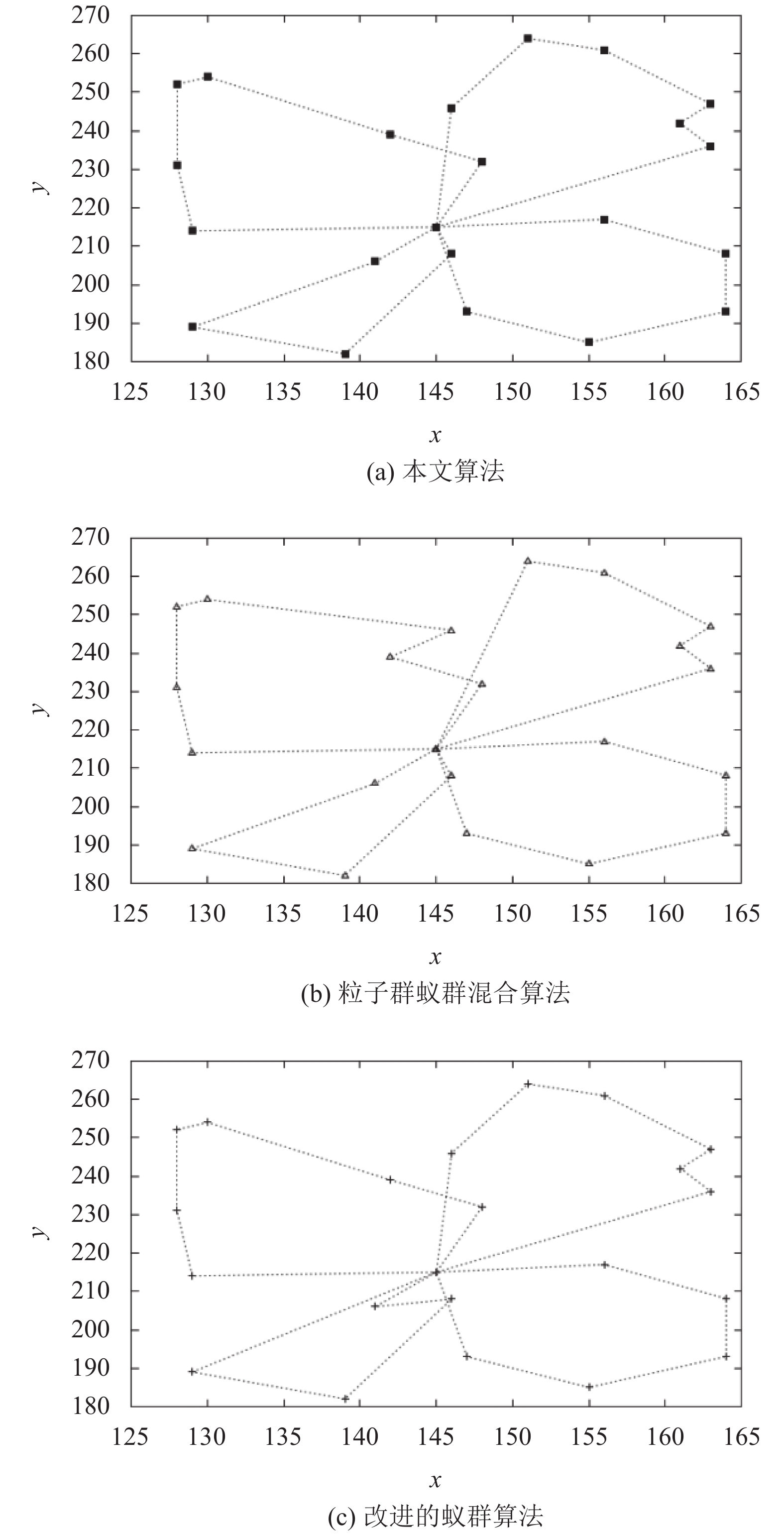
3) 案例3(eil22): 某配送中心(编号为0)用4辆装置量为6 ×103 kg的车辆对21个客户配送货物. 其余参数的设置详见参考文献[20]. 得到的最优解最优路径如图5所示.
图5(a)为本文算法, 最优路径长度为373.661, (b)为粒子群蚁群混合算法[20], 最优路径长度为375.812, (c)为改进蚁群算法[21], 最优路径长度为381.6895.
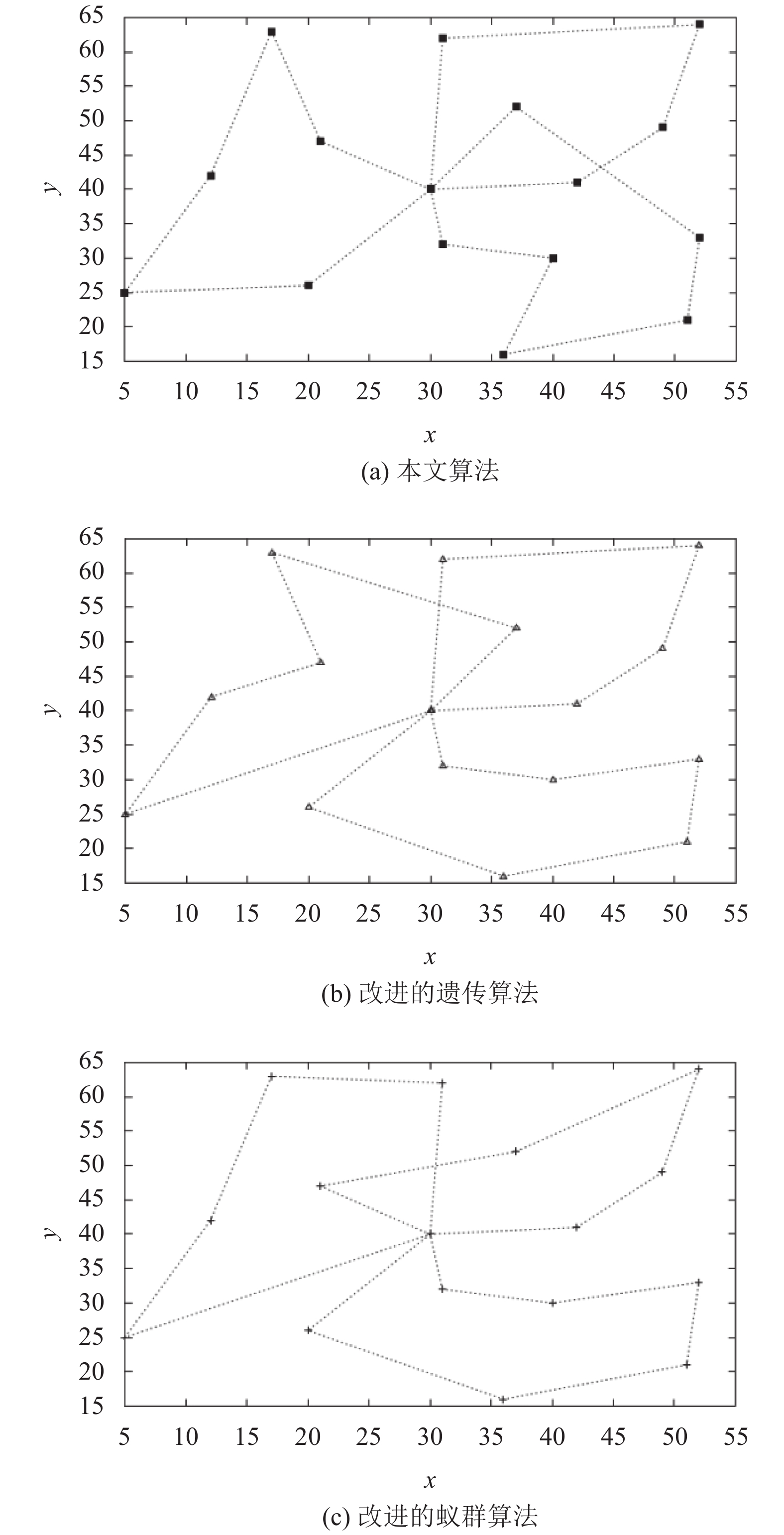
|
图 4 本文算法与其他算法的最优路径 |
5 结束语
本文通过对ACO设置信息素的动态更新阈值, 利用局部最优解不断奖惩路径进行信息素的更新, 同时采用轮盘赌方法不断跳出局部最优, 不仅可以保证可行解的多样性, 还可以加快最优解的收敛速度. 另一方面, 把客户需求量等一些因素加入禁忌表及可行解的构造过程, 从而最大程度优化初始解, 通过对概率公式进行改进, 避免某些路径的信息素挥发迅速造成数据计算的溢出. 同时采用颜色Petri网对改进后的算法进行建模仿真, 并通过实例与其他改进算法进行比较, 实验表明, 该工具操作简单, 方便, 改进后的算法收敛速度快, 能够更好地解决VRP问题, 并且在一定程度上确保模型的可扩展性.
|
图 5 本文算法与其他算法的最优路径 |
| [1] |
Toth P, Vigo D. Vehicle routing: Problems, methods, and applications. 2nd ed. Philadelphia, American: Society for Industrial and Applied Mathematics, 2014.
|
| [2] |
Dorigo M, Di Caro G. Ant colony optimization: A new meta-heuristic. Proceedings of the 1999 Congress on Evolutionary Computation. Washington, DC, USA. 1999. 1470–1477.
|
| [3] |
Gambardella LM, Taillard É, Agazzi G. MACS-VRPTW: A multiple ant colony system for vehicle routing problems with time windows. Corne D, Dorigo M, Glover F. New Ideas in Optimization. London, UK: McGraw-Hill, 1999. 63–76.
|
| [4] |
赵群. 基于改进混合蚁群算法的车辆路径问题研究[硕士学位论文]. 合肥: 合肥工业大学, 2015.
|
| [5] |
刘春英. 粒子群融合蚁群算法多配送中心车辆路径研究. 吉林师范大学学报(自然科学版), 2013, 34(3): 88-91. |
| [6] |
石华瑀. 改进的蚁群算法在实际VRP中的应用研究[硕士学位论文]. 济南: 山东大学, 2012.
|
| [7] |
Yu B, Yang ZZ, Yao BZ. An improved ant colony op-timization for vehicle routing problem. European Journal of Operational Research, 2009, 196(1): 171-176. DOI:10.1016/j.ejor.2008.02.028 |
| [8] |
葛斌. 求解车辆路径问题的蚁群优化算法研究及应用[博士学位论文]. 合肥: 合肥工业大学, 2016.
|
| [9] |
周和平, 陈亮. 求解CVRP问题的一种改进启发式蚁群算法. 后勤工程学院学报, 2015, 31(4): 80-84, 89. DOI:10.3969/j.issn.1672-7843.2015.04.014 |
| [10] |
Dhawan C, Kumar Nassa V. Review on vehicle routing problem using ant colony optimization. International Journal of Advanced Research in Computer Science, 2014, 5(6): 74-78. |
| [11] |
Petri CA. Communication with automata[Ph.D. thesis]. Bonn: University of Bonn, 1962.
|
| [12] |
郭峰, 魏光. 基于Petri网的Web服务描述及其可替换性分析. 计算机集成制造系统, 2013, 19(6): 1423-1432. |
| [13] |
范贵生, 虞慧群, 陈丽琼, 等. 基于Petri网的服务组合故障诊断与处理. 软件学报, 2010, 21(2): 231-247. |
| [14] |
曾庆田, 鲁法明, 刘聪, 等. 基于Petri网的跨组织应急联动处置系统建模与分析. 计算机学报, 2013, 36(11): 2290-2302. |
| [15] |
陆中, 孙有朝, 吴海桥. 基于着色随机时间Petri网的维修性建模方法. 机械工程学报, 2011, 47(10): 185-191. |
| [16] |
Westergaard M. CPN tools 4: Multi-formalism and extensibility. Colom JM, Desel J. Application and Theory of Petri Nets and Concurrency. Berlin, Hei-delberg: Springer, 2013. 400–409.
|
| [17] |
范小宁, 徐格宁, 杨瑞刚. 车辆配送路径优化的新型蚁群算法. 计算机工程与应用, 2011, 47(26): 232-234, 245. DOI:10.3778/j.issn.1002-8331.2011.26.066 |
| [18] |
岳苹. 基于改进蚁群算法的车辆路径优化问题研究. 工业控制计算机, 2017, 30(9): 54-55. DOI:10.3969/j.issn.1001-182X.2017.09.025 |
| [19] |
闫凯, 李爱光, 郭健. 基于混合算法的单配送中心路径优化方法. 测绘科学技术学报, 2016, 33(6): 650-653. |
| [20] |
高明芳. 基于粒子群蚁群混合算法的物流车辆路径问题研究[硕士学位论文]. 内蒙古: 内蒙古农业大学, 2016.
|
| [21] |
王书勤. 车辆路径问题的蚁群算法研究[硕士学位论文]. 重庆: 重庆大学, 2008.
|
 2018, Vol. 27
2018, Vol. 27


