2. 福建农林大学 计算机与信息学院, 福州 350002
2. College of Computer and Information Science, Fujian Agriculture and Forestry University, Fuzhou 350002, China
地震是一种常见的破坏性极大的自然灾害,严重损害着灾区人民的生命和财产安全. 在过去的数十年中, 国内外相关领域的研究人员早已开始关注地震前产生的异常, 以期对地震未来的发展趋势进行预测. 20世纪80年代前苏联学者Gorny等[1]首次报道了在中亚及东地中海地区,许多中强震前出现大面积卫星热红外辐射增强现象. 其他学者也提出了许多新的震前异常研究成果[2]. NĚMEC等[3]使用统计方法研究地震前低频电磁波数据, 发现在地震前短时间内电磁波的强度会出现异常, 这种与多种因素有关. 张元生等[4]选用静止卫星红外遥感亮温资料证明在大地震发生之前亮温变化存在明显的特征周期和振幅以及热异常分布区域. Kong等[5]使用几何移动平均鞅算法分析NOAA卫星遥感OLR数据的变化过程, 挖掘汶川地震和芦山地震前OLR数据的异常. Yeha等[6]采用多个连续GPS基准站建立一个GPS网络实时监测台湾南部地壳形变, 发现GPS信号在地震发生前很短时间内出现了系统性扰动. Kuo等[7]应用了改进的岩石圈-大气-电离层(LAI)耦合模型计算日本2011年 Tohoku-Oki 9.0级大地震发生前的电离层总电子含量, 并将计算结果与所报道的TEC观测结果进行比较, 以研究地震前电离层TEC异常. 文献[8]中使用涡流场计算和小波变换检测地震前OLR数据的异常. 文献[9]中使用模糊神经算法用于检测震前电磁异常. 文献[10]中提出了基于误差和关键点的自顶向下分段算法以及基于时间邻域的局部异常因子的分析方法对地震前兆观测数据进行异常挖掘. 文献[11]中提出地面持续增温是一种相当普遍的临震前兆增温异常, 这种前兆异常的时空动态,可实时地反映于卫星热红外图象上. 文献[12]中提出使用一种非线性过滤器HMMs来提取GPS数据中可能与地震有关的异常信号, 进而达到预测地震的目的. 文献[13]提出用小波变换来识别并分析数据中的奇异点与地震的关系. Marzocchi等[14]使用贝叶斯估值方法分析地震数据, 构建地震整体预测. 钱国红[15]利用中国大陆GPS连续观测站资料,获取了2011年3月11日日本9.0级地震造成的连续站同震位移, 通过对时间序列分析发现,有明显同震位移的连续站,震前水平方向的运动速度都有放缓的趋势. 他们认为这可能是一种地震形变前兆现象. 卫星热红外异常是一种临震预报的新指标. Ouzounov等[16]通过系统地应用卫星数据分析技术, 将卫星数据分析技术应用于大地震后的图像, 从而验证TIR异常与已知的地震相关联. 从上面可以看出, 地震发生前会产生很多异常信号, 通过对地震前兆异常的研究与分析, 寻找其中蕴含的地震前兆异常信息对预测地震, 防震减灾具有重要意义.
本文的贡献主要在于: 虽然卫星遥感技术已经广泛地应用于地震科学研究, 但由于热红外遥感数据是通过卫星来监测地面的变化, 通常会受到云层等各种因素的影响, 卫星能够监测到的信号往往比较弱. 缺乏有效的热红外遥感数据处理技术来提取地震异常相关信息以及探讨震前热异常内部机制, 导致大多数的热红外卫星遥感数据没有被充分利用. 虽然已经有不少学者开始运用数据挖掘中的异常检测算法来分析地震异常, 但是通过量子漫步算法来分析震前异常的研究相对较少, 这种算法具有鲁棒性, 是一种可行的算法. 因此, 为了能够有效的识别地震热红外(射出长波辐射)异常, 本文基于数据挖掘技术的基本原理, 结合Martingale理论[17], 提出一种量子漫步概率算法来识别热红外异常特征, 然后在经过一定的信号放大来发现异常. 针对发生在中国比较具有代表性的汶川和芦山地震, 运用该算法, 对地震前后震中附近OLR数据、P值、CD值进行分析研究. 并且, 通过实验将该算法扩展到最近十年全球发生的8.0级及以上地震, 验证该算法的有效性与可靠性. 结果表明, 量子漫步算法是一种具有鲁棒性的OLR异常变化识别方法. 同时, 它对将数据挖掘算法运用于地理科学研究领域具有重要的借鉴意义.
1 相关数据本文研究的对象是发生在中国的2008年5月12日汶川大地震和2013年4月20日芦山大地震,以及从2005年6月到2014年9月期间全球发生的8级及以上中的16个地震. 具体地震相关数据如表1所示.
2 研究方法量子漫步作为量子信息领域的一个重要分支, 是经典随机漫步向量子场景转变的概括. 量子漫步大致分为离散量子漫步和连续量子漫步两类. 本文所用的是在直线上的离散量子漫步算法挖掘震前异常. 在直线上的离散量子漫步可以描述为一个维度
量子漫步异常识别方法具体实现步骤如下:
首先, 由硬币算子
| $U = {U_S} \cdot ({I_P} \otimes {U_C})$ | (1) |
| 表 1 地震相关信息 |
在每一步中, 硬币粒子都经过一次哈达玛变换, 然后, 运动粒子根据硬币粒子的状态向对应方向运动. 具体漫步规则如图1(a)~(c)所示, 从
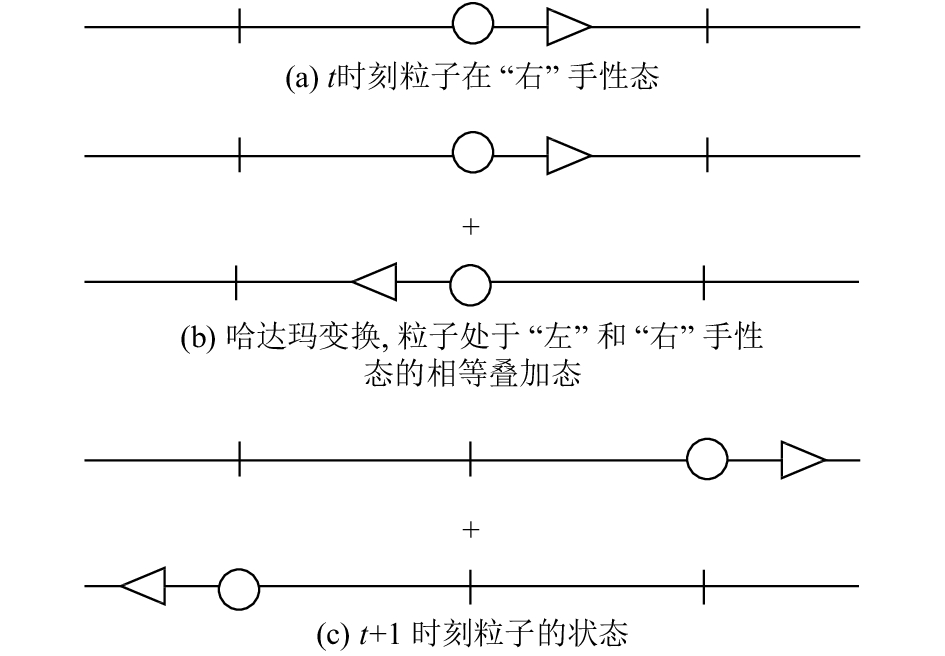
|
图 1 离散量子漫步游走规则示意图 |
其次, 经过
| $|{\psi _t}\rangle = {(U)^t}|{\psi _0}\rangle $ | (2) |
其中,
再次, 结合Martingale理论[17],对前两个步骤获得的特征序列做如下处理,定义数据点的概率变化程度(
| $CD_n^{(\varepsilon )} = \frac{{\sum\limits_{k = 1}^{100} {\prod\limits_{i = 1}^n {(\varepsilon \hat p_{i,k}^{\varepsilon - 1})} } }}{{100}}$ | (3) |
其中, 通过计算
对于无标签的时间序列数据集
| ${s_i} = s(Z,{z_i}) = \left\| {{z_i} - m} \right\|$ | (4) |
其中,
在上面定义的基础上,我们定义
| ${\hat p_{i,k}}(Z \cup \{ {z_n}\} ,{\theta _n}) = \frac{{\# \{ j\left| {{s_j} > {s_i}} \right.\} + {\theta _{i,k}}\# \{ j\left| {{s_j} = {s_i}} \right.\} }}{i}$ | (5) |
其中,
通过等式(3)的计算可以看出,
最后, 用上一步计算方法计算每一个数据点的异常度. 为了避免
| $C{D_n} \geqslant h$ | (6) |
综上所述, 基于量子漫步算法的异常挖掘算法的流程图如图2所示.
3 结果与分析(1)汶川地震和芦山地震对应的原始射出长波辐射OLR数据分别如图3(a)和图4(a)所示. 量子漫步算法中, 窗口大小
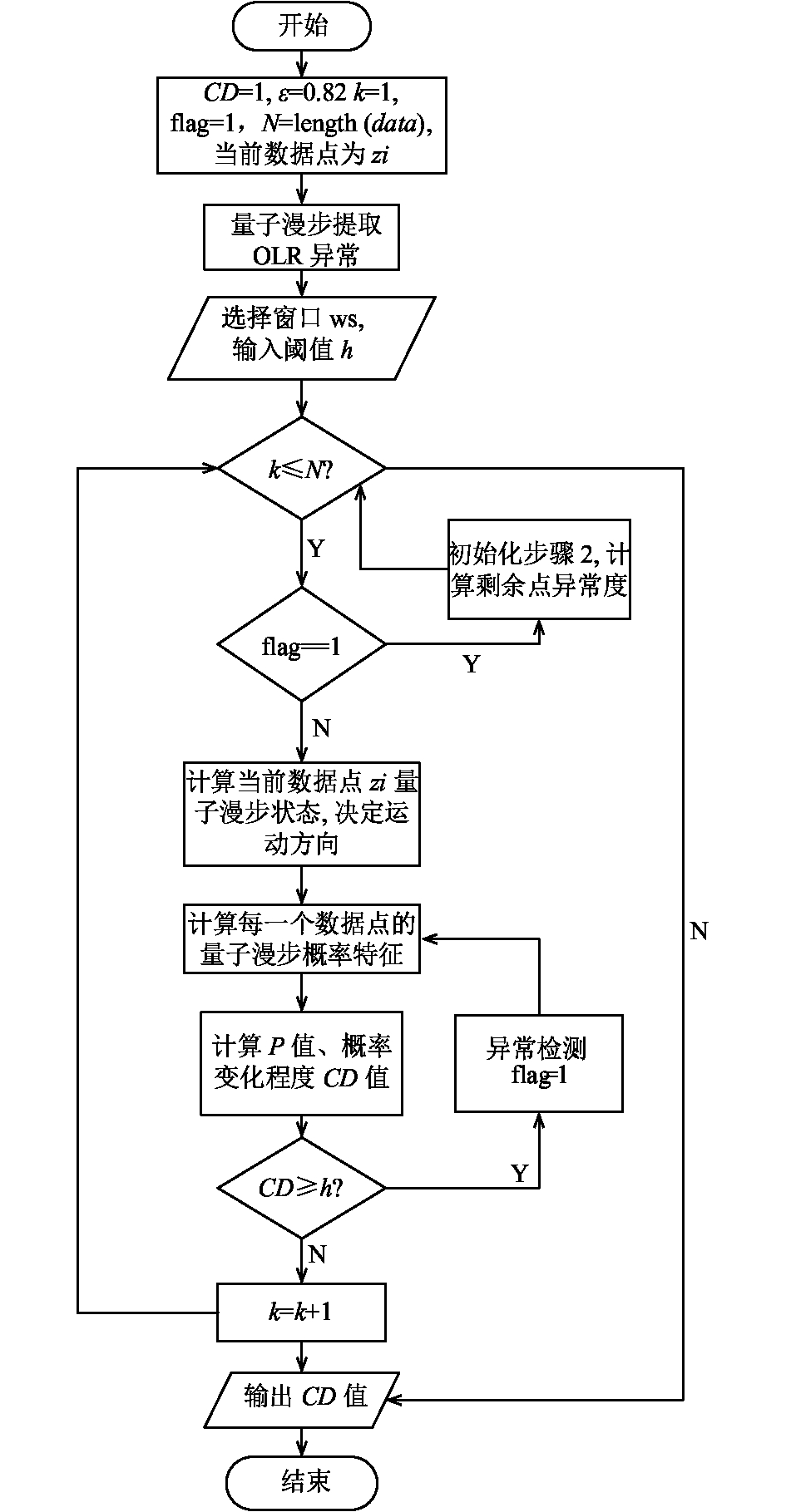
|
图 2 基于量子漫步算法的异常挖掘流程图 |
通过量子漫步算法进行初步处理OLR数据, 计算得到P值, 如图3(b)和图4(b)所示. 进一步处理特征序列, 计算数据点的概率变化程度
从图3(c)和图4(c)可以看出, 在距离地震发生时间较远的地方,
结合图3(b), 图3(c), 图4(b)和图4(c)可以看出, 当地震的P值图像在短时间内有连续且密集的上下波动的区间内会出现较大的异常值, 即
由于汶川和芦山两个地震的震中位置相对较近, 成因相似, 因此所提取的异常值
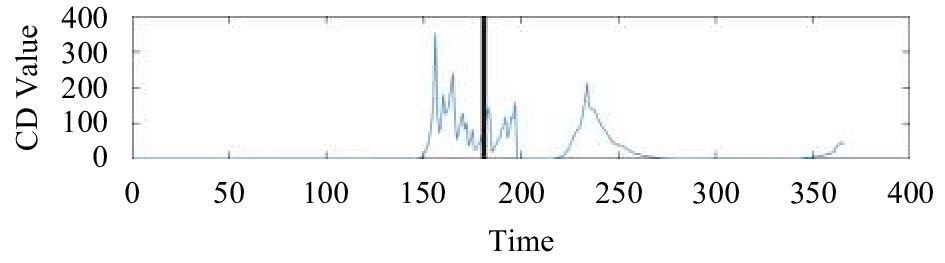
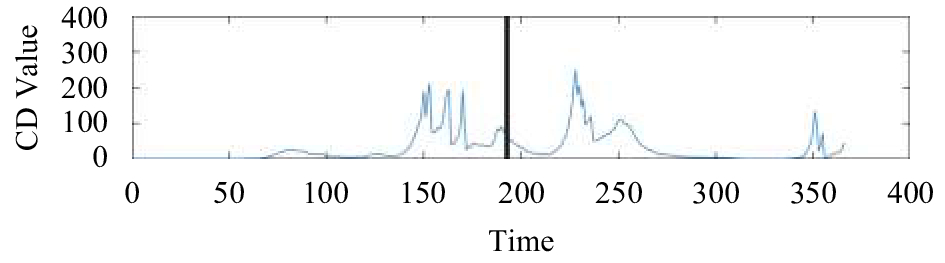
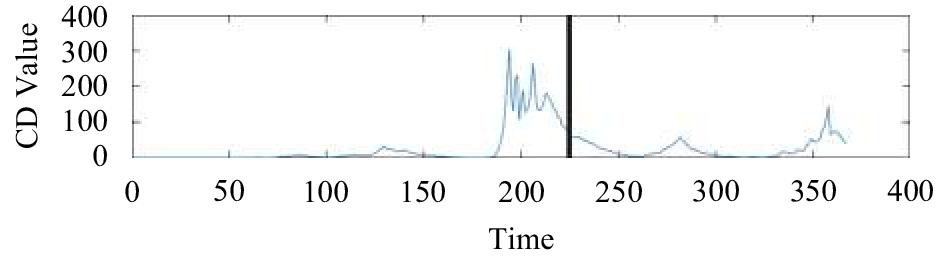
(2)为了进一步说明本文所提出的基于量子漫步算法的异常挖掘算法的可靠性和有效性, 现在扩展该算法的适用范围, 将该算法运用于分析2005年6月到2014年9月全球发生的16个8.0级及以上地震的异常数据. 受文章篇幅限制, 本文只展示其中部分地震的实验结果, 实验结果如图5~图10所示.
通过研究近10年来的时间长度为一年的OLR时间序列, 综合以上图5~图10所示图像可以看出, 各个地方CD值图像的变化趋势有相似的规律, 在距离地震发生时间较远的地方, CD值趋近于0, 几乎没有任何变化, 而在地震前后, 各个地方的CD值均出现了显著变化, 即临近地震前后会出现较大异常, 而且越大的地震异常越明显. 然而, 如果仅从地震区域的原始OLR数据图像无法直观地看出是否存在异常. 这也说明本文提出的基于量子漫步算法的异常挖掘算法几乎适用于所有地震, 具有可靠性和有效性.
(3)为了说明P值和CD值在震前出现异常和地震发生之间的因果关系, 本文针对汶川和芦山地震分别设计了对比实验.
首先, 将汶川地震与其他年份(2005年到2017年)汶川地区的P值和CD值图像进行比较. 实验结果表明, 在总共12年数据中, CD值大于100, 且小于200的有8个; 大于200且小于300的有1个; 大于300, 且小于400的有2个; 大于400的有1个. 在这12个数据中, 其中有10个异常发生的时间与汶川或其周边发生的5.0级以上地震发生时间相吻合; 出现误报的仅2个(2007和2016), 即出现异常后, 地震真正发生的概率为83.3%, 误报率为16.7%.

|
图 3 汶川地震原始OLR数据、P值和异常值CD (2008-05-12) |

|
图 4 芦山地震原始OLR数据、P值和异常值CD (2013-04-20) |
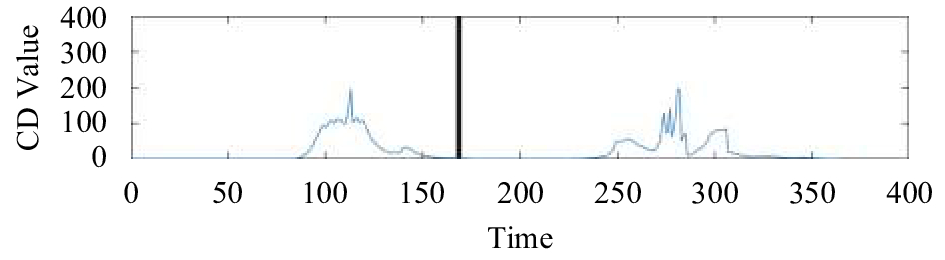
|
图 5 秘鲁中部海岸附近地震异常值CD值(2007-08-15) |
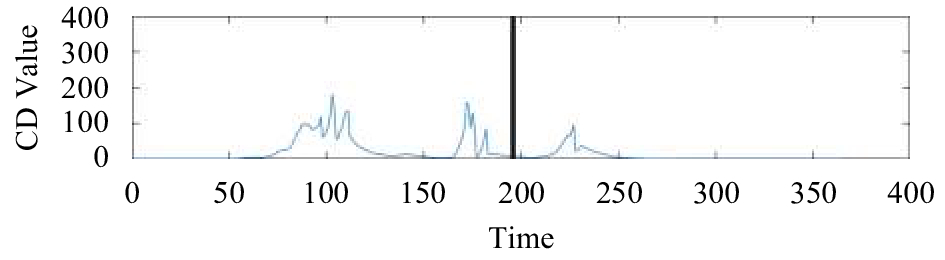
|
图 6 印尼苏门答腊南部海中地震异常值CD值 (2007-09-12) |
|
图 7 智利比奥比奥省地震异常值CD值 (2010-02-27) |
|
图 8 日本本州东海岸附近海域地震异常值CD值 (2011-03-11) |
|
图 9 苏门答腊北部附近海域地震异常值CD值 (2012-04-11) |

|
图 10 智利北部沿海岸近海地震异常值CD值 (2014-04-02) |
其次, 将芦山地震与其他年份(2005年到2017年)芦山地区的P值和CD值图像进行比较. 实验结果表明, 在总共12年数据中, CD值大于100, 且小于200的7个; 大于200且小于300的有2个; 大于300, 且小于400的有2个; 大于400的有1个. 在这12个数据中, 其中有10个异常发生的时间与汶川或其周边发生的5.0级以上地震发生时间相吻合; 出现误报的仅2个(2007和2016), 即出现异常后, 地震真正发生的概率为83.3%, 误报率为16.7%.
汶川和芦山2007年都出现大于100, 且小于200的异常, 及2016年都出现大于200且小于300, 笔者猜测可能是由于气候、温度或人为活动等原因引起的异常.
(4)为了说明本文提出的算法的优越性, 本文通过实验, 比较本文提出的基于量子漫步算法的异常挖掘算法与经典随机漫步算法提取地震异常特征的方法. 结果如下图所示. 其中, 实线曲线(图中左曲线)为100步量子漫步概率分布, 虚线曲线(图中右曲线)为随机漫步概率分布.

|
图 11 量子漫步与经典随机漫步概率模型对比 |
从图11中可以看出, 由于硬币和粒子的量子干涉效应, 在多步以后, 量子漫步算法展现出比经典随机漫步更好的一些性质. 在执行N步之后, 与经典随机漫步不同, 离散量子漫步的概率分布并不是高斯分布, 它的分布偏向左边, 比经典随机漫步收敛性快, 显然本文提出的基于量子漫步算法的异常挖掘算法更具有优势.
4 结束语本文结合Martingale理论, 提出了一种基于量子漫步算法的震前异常挖掘算法, 并运用该算法分析汶川和芦山两个地震的地震前后, 震中附近OLR数据发生的显著异常变化, 挖掘有用的震前异常信息. 从结果中可以看出, 即使原始OLR数值没有明显异常, 在地震前后一段时间内其对应的
| [1] |
Gorny VI, Salman AG, Tronin AA, et al. Terrestrial outgoing infrared radiation as an indicator of seismic activity. Proceedings of the Academy of Sciences of the USSR, 1988, 301(1): 67-69. |
| [2] |
Honkura Y, Oshiman N, Matsushima M, et al. Rapid changes in the electrical state of the 1999 Izmit earthquake rupture zone. Nature Communications, 2013, 4: 2116. DOI:10.1038/ncomms3116 |
| [3] |
NĚmec F, Santolík O, Parrot M. Decrease of intensity of ELF/VLF waves observed in the upper ionosphere close to earthquakes: A statistical study. Journal of Geophysical Research, 2009, 114(4): A04303. |
| [4] |
张元生, 郭晓, 钟美娇, 等. 汶川地震卫星热红外亮温变化. 科学通报, 2010, 55(10): 904-910. |
| [5] |
Kong XZ, Bi YX, Glass DH. Detecting seismic anomalies in outgoing long-wave radiation data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(2): 649-660. DOI:10.1109/JSTARS.2014.2363473 |
| [6] |
Yeh YL, Cheng KC, Wang WH, et al. Very short-term earthquake precursors from GPS signal interference based on the 2013 Nantou and Rueisuei earthquakes, Taiwan. Journal of Asian Earth Sciences, 2015, 114(2): 312-320. |
| [7] |
Kuo CL, Lee LC, Heki K. Preseismic TEC changes for Tohoku-Oki earthquake: Comparisons between simulations and observations. Terrestrial, Atmospheric and Oceanic Sciences, 2015, 26(1): 63-72. |
| [8] |
Xiong P, Shen XH, Bi YX, et al. Study of outgoing longwave radiation anomalies associated with Haiti earthquake. Natural Hazards and Earth System Science, 2010, 10(10): 2169-2178. |
| [9] |
Konstantaras A, Varley MR, Vallianatos F, et al. Detection of weak seismo-electric signals upon the recordings of the electrotelluric field by means of neuro-fuzzy technology. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 161-165. |
| [10] |
李正媛, 陈晶, 王丽娜, 等. 一种基于误差和关键点的地震前兆观测数据异常挖掘算法. 计算机应用研究, 2011, 28(8): 2987-2901. DOI:10.3969/j.issn.1001-3695.2011.08.051 |
| [11] |
徐秀登, 强祖基, 赁常恭. 临震卫星热红外异常与地面增温异常. 科学通报, 1991, 36(4): 291-294. DOI:10.3321/j.issn:0023-074X.1991.04.009 |
| [12] |
Wang T, Bebbington M. Identifying anomalous signals in GPS data using HMMs: An increased likelihood of earthquakes?. Comptutational Statistics and Data Analysis, 2013, 58(1): 27-44. |
| [13] |
Cervone G, Kafatos M, Napoletani D, et al. Wavelet maxima curves of surface latent heat flux associated with two recent Greek earthquakes. Natural Hazards and Earth System Science, 2004, 4(3): 359-374. DOI:10.5194/nhess-4-359-2004 |
| [14] |
Marzocchi W, Zechar JD, Jordan TH. Bayesian forecast evaluation and ensemble earthquake forecasting. Bulletin of the Seismological Society of America, 2012, 102(6): 2574-2584. DOI:10.1785/0120110327 |
| [15] |
钱国红. 量子算法及其在数据挖掘中的应用[硕士学位论文]. 杭州: 浙江工业大学, 2012. 15–18.
|
| [16] |
Ouzounov D, Bryant N, Logan T, et al. Satellite thermal IR phenomena associated with some of the major earthquakes in 1999–2003. Physics and Chemistry of the Earth, 2006, 31(4–9): 154-163. DOI:10.1016/j.pce.2006.02.036 |
| [17] |
Ho SS, Wechsler H. A martingale framework for detecting changes in data streams by testing exchangeability. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2113-2127. |
| [18] |
Nayak A, Vishwanath A. Quantum walk on the line. DIMACS Technical Report. 2000. arXiv:quant-ph/0010117.
|
| [19] |
Vork V, Nouretdinov I, Gammerman A. Testing exchangeability on-line. Proceedings of the 12th International Conference on Machine Learning. Washington, DC, USA. 2003. 768–775.
|
 2018, Vol. 27
2018, Vol. 27


