各种机器学习算法[1–3]的效果与输入空间给定的度量[4]息息相关. 例如K-means、KNN、SVM等算法需要已知的度量来反映数据间的相互关系. 比如人脸分类的问题, 假设要计算不同人脸之间的相似度或距离, 用于聚类或分类, 这时就需要构建一个距离函数去强化合适的特征如发色和脸型等; 而如果目标是识别姿势, 那么就需要构建一个捕获姿势相似度的距离函数. 为了处理各种各样的特征相似度, 可以在特定的任务通过选择合适的特征并手动构建距离函数. 然而这种方法会需要很大的人工投入, 也可能对数据的改变非常不鲁棒[5]. 度量学习作为一个理想的替代, 可以根据不同的任务来自主学习出针对某个特定任务的距离度量函数.
度量学习是机器学习领域的一个基本问题. 它对许多真实世界的应用程序至关重要. 度量学习方法广泛应用于人脸识别[6]、物体识别、音乐的相似性、人体姿势估计、信息检索、语音识别、手写体识别等领域. 目前已经有许多用于距离度量学习的算法被提出来了. 它们通常分为两类: 无监督度量学习和有监督度量学习[7,8]. 无监督的距离度量学习, 亦称为流形学习[9], 其中经典的算法有等距映射ISOMAP[10], 局部线性嵌入Local Linear Embedding (LLE)以及拉普拉斯特征映射(Laplacian Eigenmap, LE)[11]等等. 而有监督距离度量学习方面, 其中一部分有监督距离度量学习充分利用数据的标签信息来学习距离度量, 比如Information-theoretic metric learning(ITML)[12], Mahalanobis Metric Learning for Clustering (MMC)和Maximally Collapsing Metric Learning (MCML)[13], 还有的有监督距离度量学习会同时考虑数据的标签信息和数据点之间的几何关系, 比如Neighbourhood Components Analysis (NCA)[14], Large-Margin Nearest Neighbors (LMNN)[15], Relevant Component Analysis (RCA)[16], Local Linear Discriminative Analysis (Local LDA)[17]. 另外还有曾经提出过在线学习算法的Regularized Distance Metric Learning (RDML) [18]. 本文主要关注有监督的距离度量学习.
虽然在有监督的度量学习领域已经有上述这么多的研究成果, 但是很少的方法可以有效地处理噪声环境. 这些已有的算法鲁棒性受到现实中各种噪声环境的影响, 分类准确率往往不尽人意, 这时就需要一种具有良好鲁棒性的度量学习算法来对抗噪声影响. 本文结合信息论[19]中的最大相关熵准则(Maximum Correntropy Criterion, 以下简称MCC)[20], 提出了一种基于最大相关熵准则的距离度量学习算法. 最大相关熵准则在信息论中用来处理受到各种噪声影响的信号分析, 可以有效地提高信号分析的鲁棒性. 本文旨在通过将最大相关熵准则的核心高斯核函数引入到度量学习中, 通过学习得到具有良好鲁棒性的距离度量矩阵, 再使用学习到的距离度量矩阵解决一些受到各种噪声影响的分类问题. 本文将在机器学习常用数据集UCI还有人脸数据集YALEB上进行验证实验. 实验结果表明, 通过基于最大相关熵准则的度量学习方法学习到的距离度量矩阵拥有良好的鲁棒性, 可以有效提高噪声环境下的各种数据集的分类准确率.
1 相关理论 1.1 度量学习在向量空间
(1)
(2)
(3)
(4)
那么向量空间
对向量空间
| $D\left( {\overrightarrow {{x_i}} ,\overrightarrow {{x_j}} } \right) = \left\| {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right\|_2^2$ | (1) |
如果给它们都做一个线性变化将
| ${D_L}\left( {\overrightarrow {{x_i}} ,\overrightarrow {{x_j}} } \right) = \left\| {L\left( {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right)} \right\|_2^2$ | (2) |
将这个公式展开之后会有:
| ${D_L}\left( {\overrightarrow {{x_i}} ,\overrightarrow {{x_j}} } \right) = {\left( {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right)^{\rm{T}}}{L^{\rm{T}}}L\left( {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right)$ | (3) |
设定:
| $M = {L^{\rm{T}}}L$ | (4) |
通过这样的变化得到的M一定是一个正的半正定矩阵[21], 也就是不含有负的特征值. 将公式(4)带入公式(3)之后得到基于这样的M的平方距离:
| ${D_M}\left( {\overrightarrow {{x_i}} ,\overrightarrow {{x_j}} } \right) = {\left( {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right)^{\rm{T}}}M\left( {\overrightarrow {{x_i}} - \overrightarrow {{x_j}} } \right)$ | (5) |
这种形式的半度量被称为马氏度量. 通常, 这个名词被用来描述高斯分布的二次形式, 其中矩阵M是协方差矩阵的转置. 但是这里, M用来指代任何正的半正定矩阵. 公式中的距离可以被看作欧氏距离的一般化. 实际上, 如果把M设置为单位阵I, 那么马氏距离也就变为了欧氏距离.
于是, 在求解马氏距离度量时, 可以从两方面来求解, 分别是矩阵L以及矩阵M. 如果直接求解L, 那么对于L没有额外的限制, 但是如果直接求解M, 需要注意M一定是正的半正定矩阵. 其中, M或者L也被称为度量矩阵, 度量学习就是对M或者L进行学习.
1.2 相关熵在实际计算机视觉情境中, 物体识别、人脸识别等常常会受到各种噪声的干扰, 主要是因为噪声造成不可预测的自然偏差. 这也就意味着当这样的偏差或者噪声存在于样本中时, 会对计算机预测它们的分类造成严重干扰. 这些偏差无法忽视, 需要特别处理.
在信息论中, 相关熵的概念被提出用于处理受到噪声干扰的场景. 相关熵实际上和用于预估数据分布的二次熵有关. 比如:两个随机变量A和B之间的局部相似度度量为:
| ${V_\sigma }\left( {A,B} \right) = E\left[ {{k_\sigma }\left( {A - B} \right)} \right]$ | (6) |
在这里,
| ${V_{m,\sigma }}\left( {A,B} \right) = \frac{1}{m}\sum\limits_{j = 1}^m {{k_\sigma }} \left( {{A_j} - {B_j}} \right)$ | (7) |
这里,
基于公式(7), 可以进一步扩展基于样本对的相关熵准则. Liu等[20]进一步提出相关熵推导度量(correntropy induced metric), 也就是CIM. 这里的CIM和本文的度量学习并不是同一个概念. 本文关注的是进一步推导出来的最大相关熵准则.
对于任意两个同维向量A=(a1, a2, …, am)和B=(b1, b2, …, bm), 相减得到E=A–B=(e1, e2, …, em). 其中
| $\begin{aligned} CIM\left( {A,B} \right) & = {\left( {g\left( 0 \right) - \frac{1}{m}\sum\limits_{j = 1}^m {g\left( {{e_j}} \right)} } \right)^{\frac{1}{2}}} \\& = {\left( {g\left( 0 \right) - \frac{1}{m}\sum\limits_{j = 1}^m {g\left( {{a_j} - {b_j}} \right)} } \right)^{\frac{1}{2}}} \\ \end{aligned} $ | (8) |
其中,
| $\mathop {\max }\limits_\theta \frac{1}{m}\sum\limits_{j = 1}^m {g\left( {{e_j}} \right)} $ | (9) |
被称为最大相关熵准则(Maximum Correntropy Criterion, 缩写为MCC). 相关熵的核心在于高斯核函数.
2 本文方法大部分的度量学习目标都是学习到一个合适的马氏距离, 学习到的马氏距离可以进一步用于机器学习中的聚类和分类等基本问题, 可以有效提高K-means、KNN、SVM等算法效果. 但是已有的各种度量学习方法没有针对现实存在的各种噪声进行深入研究, 而噪声往往会造成不可预测的自然偏差, 这些偏差无法忽视, 需要采用一定的方法来消除它们带来的不良影响.
在信息论中, 最大相关熵准则用来处理受到各种噪声影响的信号分析. 如果可以将它引入到度量学习中, 那么理论上是可以学习到一个具有良好鲁棒性的度量矩阵. 本文尝试将最大相关熵准则引入到度量学习中, 主要在于利用它的核心, 也就是高斯核函数,构建度量学习的目标损失函数, 然后采用梯度下降法, 学习到一个鲁棒度量矩阵.
2.1 损失函数假设向量A, B是给的样本对的特征向量.
| $X = A - B$ | (10) |
公式(10)表示向量X是样本对的特征向量的差, 如果有k个样本, 那么就会有k×(k–1)/2个样本对, 用m来表示样本对的数量, 用n表示样本的特征数. 与之对应的Y表示原来的两个样本是否是同一类, 如果是同一类,
在将最大相关熵准则引入度量学习之后,优化目标函数为
| $\mathop {\max }\limits_L \left( {\frac{1}{n}\sum\limits_{t = 1}^m {{y_t}\sum\limits_{i = 1}^n {g\left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right)} } } \right)$ | (11) |
为保证稳定性[21, 22], 同时防止过拟合, 加入稀疏项(目标矩阵的F范式的平方)后得到优化目标函数为:
| $\mathop {\max }\limits_L \left( {\frac{1}{n}\sum\limits_{t = 1}^m {{y_t}\sum\limits_{i = 1}^n {g\left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right)} } - \lambda \left\| L \right\|_F^2} \right)$ | (12) |
或者用求最小化目标函数来表示为:
| $\mathop {\min }\limits_L \left( { - \frac{1}{n}\sum\limits_{t = 1}^m {{y_t}\sum\limits_{i = 1}^n {g\left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right)} } + \lambda \left\| L \right\|_F^2} \right)$ | (13) |
其中,
| $g\left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left( { - \frac{{{x^2}}}{{2{\sigma ^2}}}} \right)$ | (14) |
梯度下降法在求解机器学习算法的模型参数, 即无约束优化问题时, 梯度下降(Gradient Descent)是最常采用的方法之一. 在机器学习算法中,在最小化损失函数时, 可以通过梯度下降法来一步步的迭代求解, 得到最小化的损失函数和模型参数值.
梯度下降法和梯度上升法是可以互相转化的. 比如我们需要求解损失函数
梯度下降法的算法过程:
(1)确定当前位置的损失函数的梯度, 对于
| ${{\partial f\left( {{\theta _1},{\theta _2}, \cdots ,{\theta _n}} \right)}/{\partial {\theta _i}}}$ |
(2)用步长a乘以损失函数的梯度, 得到当前位置下降的距离, 即
(3)确定是否所有的
(4)更新所有的
| ${{{\theta _i} = {\theta _i} - a * \partial f\left( {{\theta _1},{\theta _2}, \cdots ,{\theta _n}} \right)}/{\partial {\theta _i}}}$ |
在将梯度下降法用于损失函数的处理中,为了合理的使用梯度下降法, 采用min形式的目标函数.
将高斯核函数(14)代入公式(13)中最后得到的损失函数是:
| $\mathop {\min }\limits_L \left( { - \frac{1}{n}\sum\limits_{t = 1}^m {{y_t}\sum\limits_{i = 1}^n {\exp \left( { - \frac{{{{\left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right)}^2}}}{{2{\sigma ^2}}}} \right)} } + \lambda \left\| L \right\|_F^2} \right)$ | (15) |
对这个损失函数求梯度, 也就是对目标度量矩阵的每一行求偏导, 得到:
| $\frac{1}{{\sqrt {2\pi } {\sigma ^3}}}\frac{1}{n}\sum\limits_{t = 1}^m {\overrightarrow {{x_t}} } \left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right){y_t}\exp \left( { - \frac{{{{\left( {\overrightarrow {{L_i}} \cdot {{\overrightarrow {{x_t}} }^{\rm{T}}}} \right)}^2}}}{{2{\sigma ^2}}}} \right) + 2\lambda \overrightarrow {{L_i}} $ | (16) |
相关熵的核心在于高斯核函数, 高斯函数的形状如图1所示.

|
图 1 高斯函数 |
变量
| ${K_\sigma }\left( {{x_1},{x_2}} \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left( { - \frac{{{{\left\| {{x_1} - {x_2}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$ | (17) |
不妨设定
从图1中, 可以明显看出
分析相关熵拥有良好的鲁棒性的原因: 假如
算法1. 基于最大相关熵准则的鲁棒度量学习算法
输入: 样本
输出: L
1) 样本转化为样本对
2) 初始化L为单位阵I, 依据公式(15)计算初始损失函数值loss.
3) 选择学习速率r开始梯度下降, 得到新的目标度量矩阵L_new和损失函数loss1.
4) 再次梯度下降, 得到新的目标度量矩阵和损失函数loss2.
5) 重复2)、3)步骤, 直到满足
6) 最后得到的L_new也就是需要的最后输出L.
3 实验结果与分析 3.1 参数设置通过公式可以看出, 实验有4个主要参数,分别是正则化项系数
最开始判定的正则项系数
由于有4个主要参数需要调整, 实验中先调整变化范围小的r和
与本文中所提出的基于最大相关熵准则的度量学习算法做对比实验的是ITML、LMNN和RDML三种算法.
ITML是Davis JV等人在文献[12]中提出的与信息论相关的度量学习算法. 算法的思想是在距离函数约束条件下将两个多元高斯之间的差分相对熵(KL散度)最小化, 从而形成待解问题. 然后将这个问题转化为一个特定的Bregman优化问题来表达求解. 实验中需要设置的参数是松弛系数. 实验时设置松弛系数按10的指数阶变化, 然后通过验证集选出最佳松弛系数, 最后应用到测试集中. 由于ITML每次实验得到的结果并不固定,因此每组做10次实验, 然后取平均值.
LMNN是Weinberger KQ等人在文献[15]中提出的经典度量学习算法. 算法的核心思想在于, Metric是以k个最近邻总是属于同一个类, 而不同类的例子是大幅分开为目标来进行训练的. 另外此方法在处理多分类的问题时不需要修改或扩展. 实验中该方法的参数直接通过验证集学习到, 然后应用到测试集中. 由于LMNN每次实验得到的结果也不固定, 同样每组做10次实验, 然后取平均值.
RDML是Jin R等在文献[18]中提出的度量学习算法. 算法提出在适当的约束下, 正则化距离度量学习可以独立于维度, 使其适合处理高维数据. 在实验中需要设置的参数是正则项系数. 实验时设置正则项系数按10的指数阶变化, 然后通过验证集选出最佳正则项系数, 最后应用到测试集中.
3.3 UCI标准数据集上的实验结果数据预处理: 为了模拟实际噪声影响, 本文在实验中给实验数据集全部加了高斯噪声.具体的加噪方法是: 先选择需要加噪的样本和特征维度, 求取对应特征维度的平均值mean和方差std, 利用Matlab中的随机函数normrnd, 给这些样本的对应维度的特征加上[0,std]之间的噪声. 加噪样本数量比例是50%, 加噪特征比例是50%. 在专用的机器学习数据集UCI上选取了4个数据集car evaluation database, teaching assistant evaluation database, balance scale weight & distance database, glass identification evaluation database (下载地址: http://archive.ics.uci.edu/ml/index.php), 在这四个数据集上分别进行实验. 其中car evaluation database是汽车评价数据集, 有6个特征, 分别是购买价格、维修价格、车门数量、座位数、后备箱大小以及安全性. 汽车种类共有4类, 一共1728个样本. Teaching assistant evaluation database是助教评价数据集, 一共5个特征, 分别是助教母语、课程指导员、课程、是否夏季课程以及班级大小. 该数据集一共分3类, 一共151个样本. Balance scale weight & distance database是天平倾向数据集, 有4个特征, 分别是左边重量、左边距中心距离、右边重量、右边距中心距离. 天平倾向种类一共3类, 共625个样本. Glass identification evaluation database是玻璃杯评价数据集, 一共10个特征. 玻璃杯种类一共分7类, 一共214个样本.
进行对比实验的是上文中提到的度量学习中领先的三种各具特色的方法ITML,LMNN,RDML. 将这三种方法与本文提出的算法应用到上述4个标准数据集中, 分别学习到合适的度量矩阵, 最后使用简单的KNN分类中, 比较实验结果. 实验结果如表1、2、3、4所示.
| 表 1 在car evaluation database上的实验结果 |
| 表 2 在teaching assistant evaluation database上的实验结果 |
| 表 3 在balance scale weight & distance database上的实验结果 |
| 表 4 在glass identification evaluation database 上的实验结果 |
如表1、2、3、4所示, 在car evaluation database, teaching assistant evaluation database, balance scale weight & distance database, glass identification evaluation database这四个数据集上的实验结果证明本文提出的基于最大相关熵准则的度量学习算法相比已有的度量学习算法LMNN\RDML\ITML在处理有噪声的数据集时分类准确率更高. 虽然在 表1的car evaluation database上的实验出现偶尔的RDML的领先情况, 然而任何方法都不能保证在所有的数据集上都有效, 出现较小的波动是很正常的事情. 可能这个数据集更适合RDML或者本次随机加噪的结果刚好对RDML的影响较小, 使得RDML的分类准确率没有下降很多. 实验中更需要关注的是多次实验的平均结果, 很明显的是在平均结果方面, 本文算法都对另外三种算法保持领先优势.
表1、2、3、4已经证明了本文提出的算法在处理受到高斯噪声的影响的标准数据集分类问题时, 可以有效地提高分类准确率. 接下来, 详细地拓展实验, 在glass identification evaluation database上进行2组进阶实验, 观察比较随着噪声的变化, 不同的度量学习算法对比本文提出的算法, 分类准确率的变化趋势.
进阶试验1, 固定加噪样本数量比例为50%, 在不同加噪特征比例上进行试验, 不同比例均进行3次实验, 然后取平均值, 实验结果如图2所示.
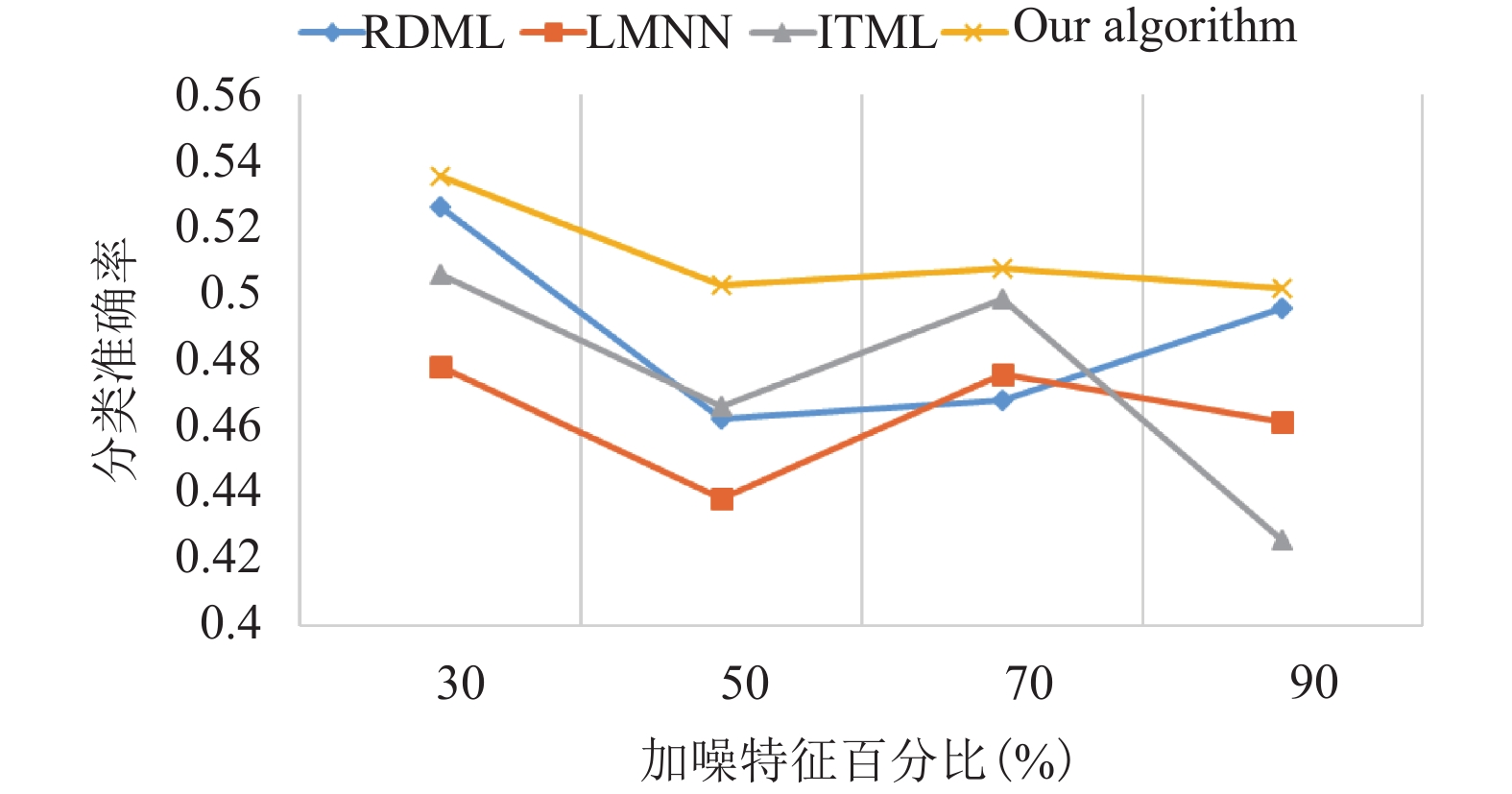
|
图 2 分类准确率随加噪特征百分比变化图 |
从图2中可以看出, 随着加噪特征百分比的增多, 本文的算法通常都领先其他算法, 而且随着加噪特征百分比的增多, 识别准确率的变化不像其他算法那样有较大的波动, 识别准确率依然保持稳定, 说明本文算法的鲁棒性良好.
进阶试验2, 固定加噪特征比例为50%, 在不同加噪样本数量比例上进行实验, 同样的不同比例均进行3次实验, 然后取平均值.实验结果如图3所示.
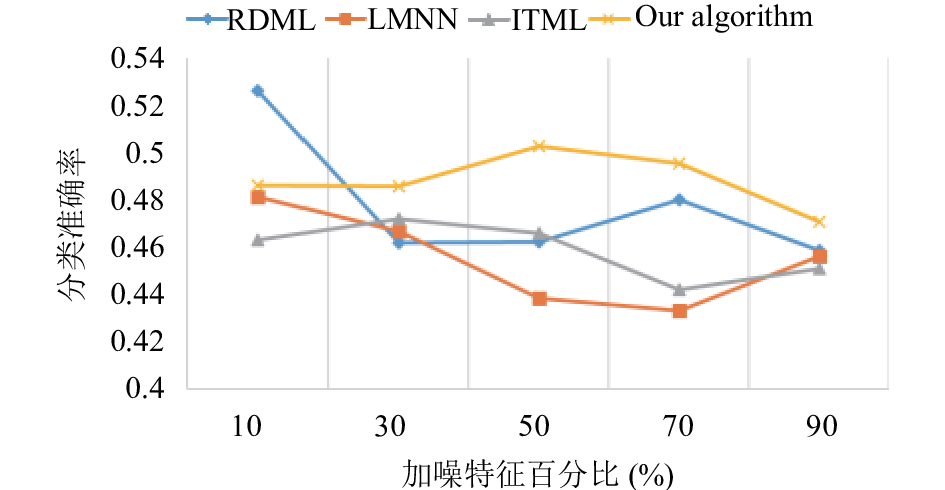
|
图 3 分类准确率随着加噪样本数量百分比变化图 |
从图3中可以看出, 随着加噪样本数量百分比的增多, 本文的算法的分类准确率逐渐开始领先其他算法, 并且随着夹杂噪声的样本数量的增加, 分类准确率并不会产生较大的波动, 变化较为平稳. 这说明本文的算法对噪声的鲁棒性是更好的.
3.4 人脸数据集YALEB实验在上述UCI的4个标准数据集上验证算法有效性之后, 接下来将在标准人脸数据库上验证. 实验选定YALEB数据集(下载地址: http://vision.ucsd.edu/~leekc/ExtYaleDatabase/ExtYaleB.html或者http://download.csdn.net/download/fantacy08/8077733). 数据集由耶鲁大学提供, 该数据集经常用于人脸检测和人脸识别. 数据集一共包含38个人, 每个人有不同光照条件下的64张人脸图片, 每张图片经过裁剪后是32×32的图片. 下载的人脸图片需要进行一定的预处理, 本文的处理方法分为两步. 其一是加噪部分, 仍然和上述4个小数据集的加噪方法一样, 加噪样本数量百分比和加噪特征百分比都选择50%; 其二是降维部分, 本文选择PCA降维处理, 提取前100个特征用于接下来的分类实验.
| 表 5 在YaleB上的实验结果 |
从表5中也可以看出, 本文提出的算法相比已有的LMNN, RDML, ITML, 在处理这样的加噪人脸时, 分类准确率同样得到了提高. 并且实验结果比较稳定, 基本不会因受到噪声的干扰而产生较大的波动. 说明了本文算法的鲁棒性经过实验验证是成功的. 虽然在表5中的实验二出现偶尔的ITML领先的情况, 实验中要考虑到ITML每次实验的结果不固定, 通常是10次实验的平均值, 因此可能出现选中的10次实验的分类准确率都较高, 进而引起平均准确率的提升. 另外单次的实验无法反映一般性, 多次实验的平均值是更为重要的判断依据. 从表5中可以明显看出4次实验的平均值中, 本文的算法保持领先优势.
接下来, 与上述glass数据集一样, 进行拓展试验, 观察人脸分类准确率随着加噪特征百分比的变化趋势. 实验结果如图4所示.

|
图 4 人脸分类准确率随人脸加噪特征百分比变化图 |
从图4可以看出, 本文提出的算法在处理加噪人脸图像时, 分类准确率往往保持领先, 同时对比另外三种度量学习方法, 分类准确率变化很稳定, 不会大幅度变化, 鲁棒性良好.这说明本文算法不仅在处理UCI上的一些小型数据集有很好的效果, 对于大型的人脸数据集同样有良好的效果.
4 总结本文引入信息论中的最大相关熵准则, 提出了基于最大相关熵准则的鲁棒度量学习算法. 经过实验验证, 该方法在处理噪声环境中的分类问题时, 有优秀的表现, 是一个可行的算法. 之后, 我们计划将MCC引入深度学习, 也可以将MCC与深度学习, 度量学习三者结合起来, 期望得到效果更好的鲁棒度量学习方法或者深度学习框架.
| [1] |
周志华. 机器学习. 北京: 清华大学出版社, 2016.
|
| [2] |
李航. 统计学习方法. 北京: 清华大学出版社, 2012.
|
| [3] |
谢剑斌, 兴军亮, 张立宁, 等. 视觉机器学习20讲. 北京: 清华大学出版社, 2015.
|
| [4] |
Yang L. Distance metric learning: A comprehensive survey [Thesis]. Michigan: Michigan State University, 2006.
|
| [5] |
He R, Zheng WS, Hu BG. Maximum correntropy criterion for robust face recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1561-1576. DOI:10.1109/TPAMI.2010.220 |
| [6] |
Zhao W, Chellappa R, Phillips PJ, et al. Face recognition: A literature survey. ACM Computing Surveys, 2003, 35(4): 399-458. DOI:10.1145/954339 |
| [7] |
沈媛媛, 严严, 王菡子. 有监督的距离度量学习算法研究进展. 自动化学报, 2014, 40(12): 2673-2686. |
| [8] |
战扬, 金英, 杨丰. 基于监督的距离度量学习方法研究. 信息技术, 2011(12): 21-23. DOI:10.3969/j.issn.1009-2552.2011.12.006 |
| [9] |
Saul LK, Roweis ST. Think globally, fit locally: Unsupervised learning of low dimensional manifolds. Journal of Machine Learning Research, 2003, 4: 119-155. |
| [10] |
Tenenbaum JB, De Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science, 2000, 290(5500): 2319-2323. DOI:10.1126/science.290.5500.2319 |
| [11] |
Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering. NIPS’01 Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. Vancouver, British Columbia, Canada. 2001. 585–591.
|
| [12] |
Davis JV, Kulis B, Jain P, et al. Information-theoretic metric learning. Proceedings of the 24th International Conference on Machine Learning. Corvalis, OR, USA. 2007. 209–216.
|
| [13] |
Globerson A, Roweis ST. Metric learning by collapsing classes. In: Weiss Y, Sch lkopf B, Platt J, eds. Advances in Neural Information Processing Systems. Cambridge, MA, USA. MIT Press, 2006. 451–458.
|
| [14] |
Goldberger J, Roweis S, Hinton G, , et al. Neighbourhood components analysis. In: Saul LK, Weiss Y, Bottou L, eds. Advances in Neural Information Processing Systems. Cambridge, MA, USA. MIT Press, 2005. 513–520.
|
| [15] |
Weinberger KQ, Saul LK. Distance metric learning for large margin nearest neighbor classification. Journal of Machine Learning Research, 2009, 10: 207-244. |
| [16] |
Tsang IW, Cheung PM, Kwok JT. Kernel relevant component analysis for distance metric learning. Proceedings of 2005 IEEE International Joint Conference on Neural Networks. Montreal, QB, Canada. 2005. 954–959.
|
| [17] |
Kim TK, Kittler J. Locally linear discriminant analysis for multimodally distributed classes for face recognition with a single model image. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(3): 318-327. DOI:10.1109/TPAMI.2005.58 |
| [18] |
Jin R, Wang SJ, Zhou Y. Regularized distance metric learning: Theory and algorithm. In: Bengio Y, Schuurmans D, Lafferty JD, et al, eds. Advances in Neural Information Processing Systems. Bethesda, MD, USA. MIT Press, 2009.
|
| [19] |
Erdogmus D, Principe JC. An error-entropy minimization algorithm for supervised training of nonlinear adaptive systems. IEEE Transactions on Signal Processing, 2002, 50(7): 1780-1786. DOI:10.1109/TSP.2002.1011217 |
| [20] |
Liu WF, Pokharel PP, Principe JC. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Transactions on Signal Processing, 2007, 55(11): 5286-5298. DOI:10.1109/TSP.2007.896065 |
| [21] |
Shalev-Shwartz S, Singer Y, Ng AY. Online and batch learning of pseudo-metrics. Proceedings of the Twenty-first International Conference on Machine Learning. Banff, Alberta, Canada. 2004. 94.
|
| [22] |
Bousquet O, Elisseeff A. Stability and generalization. Journal of Machine Learning Research, 2002, 2: 499-526. |
 2018, Vol. 27
2018, Vol. 27


